
Previous in Differential Equation Next in Differential Equation
Question Number 108227 by Ar Brandon last updated on 15/Aug/20
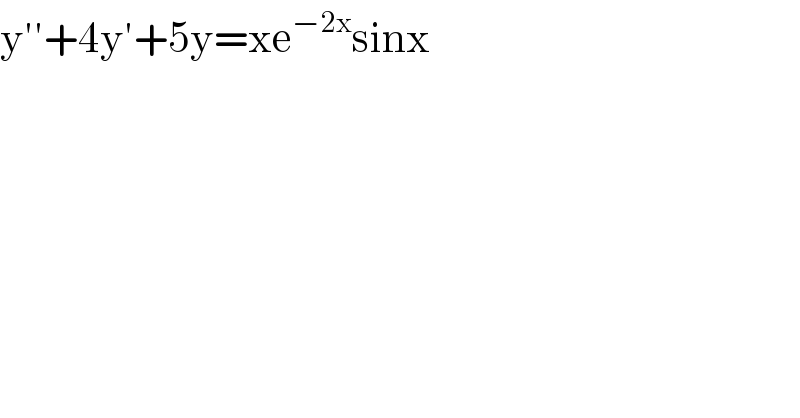
$$\mathrm{y}''+\mathrm{4y}'+\mathrm{5y}=\mathrm{xe}^{−\mathrm{2x}} \mathrm{sinx} \\ $$
Answered by mathmax by abdo last updated on 15/Aug/20

$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} +\mathrm{4r}+\mathrm{5}=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{4}−\mathrm{5}\:=−\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =−\mathrm{2}+\mathrm{i}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =−\mathrm{2}−\mathrm{i}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{e}^{−\mathrm{2x}} \left\{\mathrm{acosx}\:+\mathrm{bsinx}\right\}\:=\mathrm{a}\:\mathrm{e}^{−\mathrm{2x}} \mathrm{cosx}\:+\mathrm{be}^{−\mathrm{2x}} \mathrm{sinx}\:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{−\mathrm{2x}} \mathrm{cosx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} \mathrm{sinx}}\\{−\left(\mathrm{2cosx}\:+\mathrm{sinx}\right)\mathrm{e}^{−\mathrm{2x}} \:\:\:\:\:\:\left(\mathrm{cosx}−\mathrm{2sinx}\right)\mathrm{e}^{−\mathrm{2x}} }\end{vmatrix} \\ $$$$=\left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{2sinx}\:\mathrm{cosx}\:+\mathrm{2cosx}\:\mathrm{sinx}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{e}^{−\mathrm{4x}} \:=\mathrm{e}^{−\mathrm{4x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} \mathrm{sinx}}\\{\mathrm{xe}^{−\mathrm{2x}} \mathrm{sinx}\:\:\:\:\:\:\left(\mathrm{cosx}−\mathrm{2sinx}\right)\mathrm{e}^{−\mathrm{2x}} }\end{vmatrix}=−\mathrm{xe}^{−\mathrm{4x}} \mathrm{sin}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{−\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\left(\mathrm{2cosx}\:+\mathrm{sinx}\right)\mathrm{e}^{−\mathrm{2x}} \:\:\:\:\:\:\:\:\:\mathrm{xe}^{−\mathrm{2x}} \mathrm{sinx}}\end{vmatrix}=\mathrm{xe}^{−\mathrm{4x}} \mathrm{sinx} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\mathrm{x}\:\frac{\mathrm{e}^{−\mathrm{4x}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{e}^{−\mathrm{4x}} }\mathrm{dx}\:\:=−\int\:\mathrm{x}\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=−\int\mathrm{x}\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\mathrm{dx}\:=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{x}\:\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx}\right\} \\ $$$$=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\:+\frac{\mathrm{x}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{4x}\right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{xe}^{−\mathrm{4x}} \mathrm{sinx}}{\mathrm{e}^{−\mathrm{4x}} }\mathrm{dx}\:=\int\:\mathrm{x}\:\mathrm{sin}\left(\mathrm{x}\right)\mathrm{dx}\: \\ $$$$=−\mathrm{xcosx}\:+\int\:\mathrm{cosx}\:\mathrm{dx}\:=\mathrm{sinx}−\mathrm{xcosx}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{e}^{−\mathrm{2x}} \mathrm{cosx}\left\{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\:+\frac{\mathrm{x}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{4x}\right)\right\} \\ $$$$+\mathrm{e}^{−\mathrm{2x}} \mathrm{sinx}\left\{\mathrm{sinx}\:−\mathrm{xcosx}\right\}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$
Commented by Ar Brandon last updated on 15/Aug/20
Sir, it's the first time I'm using this method. Can you please verify if I'm correct ? ��
Answered by Ar Brandon last updated on 15/Aug/20
![y′′+4y′+5y=xsin(x)e^(−2x) y_(GH) : r^2 +4r+5=0⇒r=−2±i. y_(GH) =e^(−2x) (acosx+bsinx) y_(GH) =a(e^(−2x) cosx)+b(e^(−2x) sinx)=au_1 +bu_2 y_P =a(x)u_1 +b(x)u_2 =v_1 u_1 +v_2 u_2 { ((v_1 ′u_1 +v_2 ′u_2 =0)),((v_1 ′u_1 ′+v_2 ′u_2 ′=xsin(x)e^(−2x) )) :} W(u_1 ,u_2 )= determinant ((u_1 ,u_2 ),((u_1 ′),(u_2 ′)))= determinant (((e^(−2x) cosx),(e^(−2x) sinx)),((−e^(−2x) (sinx+2cosx)),(e^(−2x) (cosx−2sinx)))) =e^(−4x) (cos^2 x−sin2x+sin^2 x+sin2x)=e^(−4x) W_1 = determinant ((0,u_2 ),((xe^(−2x) sinx),(u_2 ′)))=−xe^(−4x) sin^2 x W_2 = determinant ((u_1 ,0),((u_1 ′),(xe^(−2x) sinx)))=xe^(−4x) sinxcosx v_1 =∫(W_1 /W)dx=∫((−xe^(−4x) sin^2 x)/e^(−4x) )dx=∫−xsin^2 xdx =(1/2)∫x(cos2x−1)dx=(1/2)[x(((sin2x)/2)−x)−∫(((sin2x)/2)−x)dx] 2v_1 =((xsin2x)/4)−x^2 +((cos2x)/4)+(x^2 /2)+K_1 v_2 =∫(W_2 /W)dx=∫((xe^(−4x) sinxcosx)/e^(−4x) )dx=(1/2)∫2xsinxcosxdx =(1/2)∫xsin2xdx=(1/2)[−x(((cos2x)/2))+∫(((cos2x)/2))dx 2v_2 =−x(((cos2x)/2))+((sin2x)/4)+K_2 Y_G =y_(GH) +y_P Y_G =e^(−2x) (acosx+bsinx)+(1/2)(((xsin2x)/4)+((cos2x)/4)−(x^2 /2)+K_1 )e^(−2x) cosx +(1/2)(−x(((cos2x)/2))+((sin2x)/4)+K_2 )e^(−2x) sinx](Q108260.png)
$$\mathrm{y}''+\mathrm{4y}'+\mathrm{5y}=\mathrm{xsin}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{y}_{\mathrm{GH}} :\:\mathrm{r}^{\mathrm{2}} +\mathrm{4r}+\mathrm{5}=\mathrm{0}\Rightarrow\mathrm{r}=−\mathrm{2}\pm\mathrm{i}.\:\mathrm{y}_{\mathrm{GH}} =\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{acosx}+\mathrm{bsinx}\right) \\ $$$$\mathrm{y}_{\mathrm{GH}} =\mathrm{a}\left(\mathrm{e}^{−\mathrm{2x}} \mathrm{cosx}\right)+\mathrm{b}\left(\mathrm{e}^{−\mathrm{2x}} \mathrm{sinx}\right)=\mathrm{au}_{\mathrm{1}} +\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{y}_{\mathrm{P}} =\mathrm{a}\left(\mathrm{x}\right)\mathrm{u}_{\mathrm{1}} +\mathrm{b}\left(\mathrm{x}\right)\mathrm{u}_{\mathrm{2}} =\mathrm{v}_{\mathrm{1}} \mathrm{u}_{\mathrm{1}} +\mathrm{v}_{\mathrm{2}} \mathrm{u}_{\mathrm{2}} \\ $$$$\begin{cases}{\mathrm{v}_{\mathrm{1}} '\mathrm{u}_{\mathrm{1}} +\mathrm{v}_{\mathrm{2}} '\mathrm{u}_{\mathrm{2}} =\mathrm{0}}\\{\mathrm{v}_{\mathrm{1}} '\mathrm{u}_{\mathrm{1}} '+\mathrm{v}_{\mathrm{2}} '\mathrm{u}_{\mathrm{2}} '=\mathrm{xsin}\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} }\end{cases} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{u}_{\mathrm{1}} }&{\mathrm{u}_{\mathrm{2}} }\\{\mathrm{u}_{\mathrm{1}} '}&{\mathrm{u}_{\mathrm{2}} '}\end{vmatrix}=\begin{vmatrix}{\mathrm{e}^{−\mathrm{2x}} \mathrm{cosx}}&{\mathrm{e}^{−\mathrm{2x}} \mathrm{sinx}}\\{−\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{sinx}+\mathrm{2cosx}\right)}&{\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{cosx}−\mathrm{2sinx}\right)}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{e}^{−\mathrm{4x}} \left(\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin2x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{sin2x}\right)=\mathrm{e}^{−\mathrm{4x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}}&{\mathrm{u}_{\mathrm{2}} }\\{\mathrm{xe}^{−\mathrm{2x}} \mathrm{sinx}}&{\mathrm{u}_{\mathrm{2}} '}\end{vmatrix}=−\mathrm{xe}^{−\mathrm{4x}} \mathrm{sin}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{u}_{\mathrm{1}} }&{\mathrm{0}}\\{\mathrm{u}_{\mathrm{1}} '}&{\mathrm{xe}^{−\mathrm{2x}} \mathrm{sinx}}\end{vmatrix}=\mathrm{xe}^{−\mathrm{4x}} \mathrm{sinxcosx} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}=\int\frac{−\mathrm{xe}^{−\mathrm{4x}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{e}^{−\mathrm{4x}} }\mathrm{dx}=\int−\mathrm{xsin}^{\mathrm{2}} \mathrm{xdx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{x}\left(\mathrm{cos2x}−\mathrm{1}\right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{x}\left(\frac{\mathrm{sin2x}}{\mathrm{2}}−\mathrm{x}\right)−\int\left(\frac{\mathrm{sin2x}}{\mathrm{2}}−\mathrm{x}\right)\mathrm{dx}\right] \\ $$$$\mathrm{2v}_{\mathrm{1}} =\frac{\mathrm{xsin2x}}{\mathrm{4}}−\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{cos2x}}{\mathrm{4}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{K}_{\mathrm{1}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}=\int\frac{\mathrm{xe}^{−\mathrm{4x}} \mathrm{sinxcosx}}{\mathrm{e}^{−\mathrm{4x}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{2xsinxcosxdx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{xsin2xdx}=\frac{\mathrm{1}}{\mathrm{2}}\left[−\mathrm{x}\left(\frac{\mathrm{cos2x}}{\mathrm{2}}\right)+\int\left(\frac{\mathrm{cos2x}}{\mathrm{2}}\right)\mathrm{dx}\right. \\ $$$$\mathrm{2v}_{\mathrm{2}} =−\mathrm{x}\left(\frac{\mathrm{cos2x}}{\mathrm{2}}\right)+\frac{\mathrm{sin2x}}{\mathrm{4}}+\mathrm{K}_{\mathrm{2}} \\ $$$$\mathrm{Y}_{\mathrm{G}} =\mathrm{y}_{\mathrm{GH}} +\mathrm{y}_{\mathrm{P}} \\ $$$$\mathrm{Y}_{\mathrm{G}} =\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{acosx}+\mathrm{bsinx}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{xsin2x}}{\mathrm{4}}+\frac{\mathrm{cos2x}}{\mathrm{4}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{K}_{\mathrm{1}} \right)\mathrm{e}^{−\mathrm{2x}} \mathrm{cosx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{x}\left(\frac{\mathrm{cos2x}}{\mathrm{2}}\right)+\frac{\mathrm{sin2x}}{\mathrm{4}}+\mathrm{K}_{\mathrm{2}} \right)\mathrm{e}^{−\mathrm{2x}} \mathrm{sinx} \\ $$
Commented by mathmax by abdo last updated on 15/Aug/20
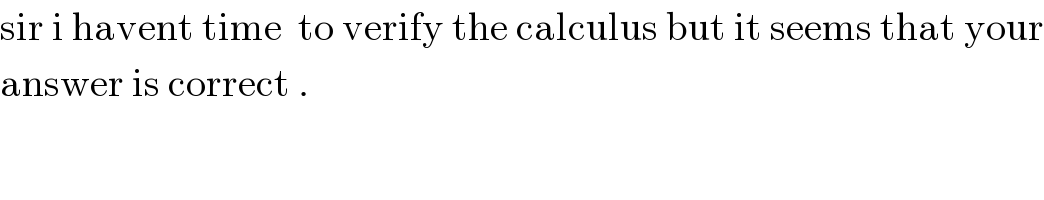
$$\mathrm{sir}\:\mathrm{i}\:\mathrm{havent}\:\mathrm{time}\:\:\mathrm{to}\:\mathrm{verify}\:\mathrm{the}\:\mathrm{calculus}\:\mathrm{but}\:\mathrm{it}\:\mathrm{seems}\:\mathrm{that}\:\mathrm{your} \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{correct}\:. \\ $$
Commented by Ar Brandon last updated on 15/Aug/20
Thanks for your reply ��
