
Question and Answers Forum
Question Number 108228 by bemath last updated on 15/Aug/20
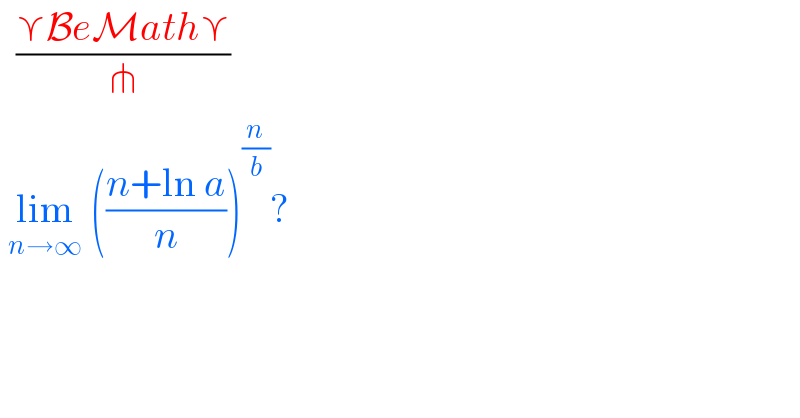
Answered by Dwaipayan Shikari last updated on 15/Aug/20
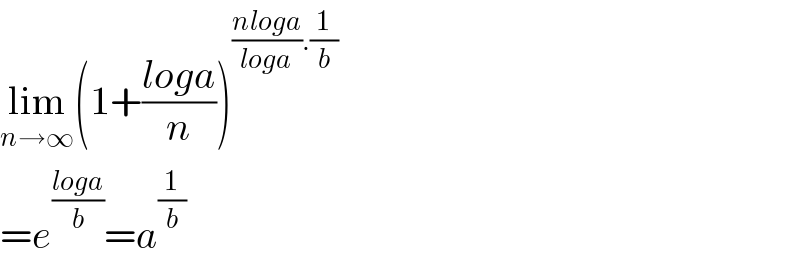
Answered by john santu last updated on 15/Aug/20
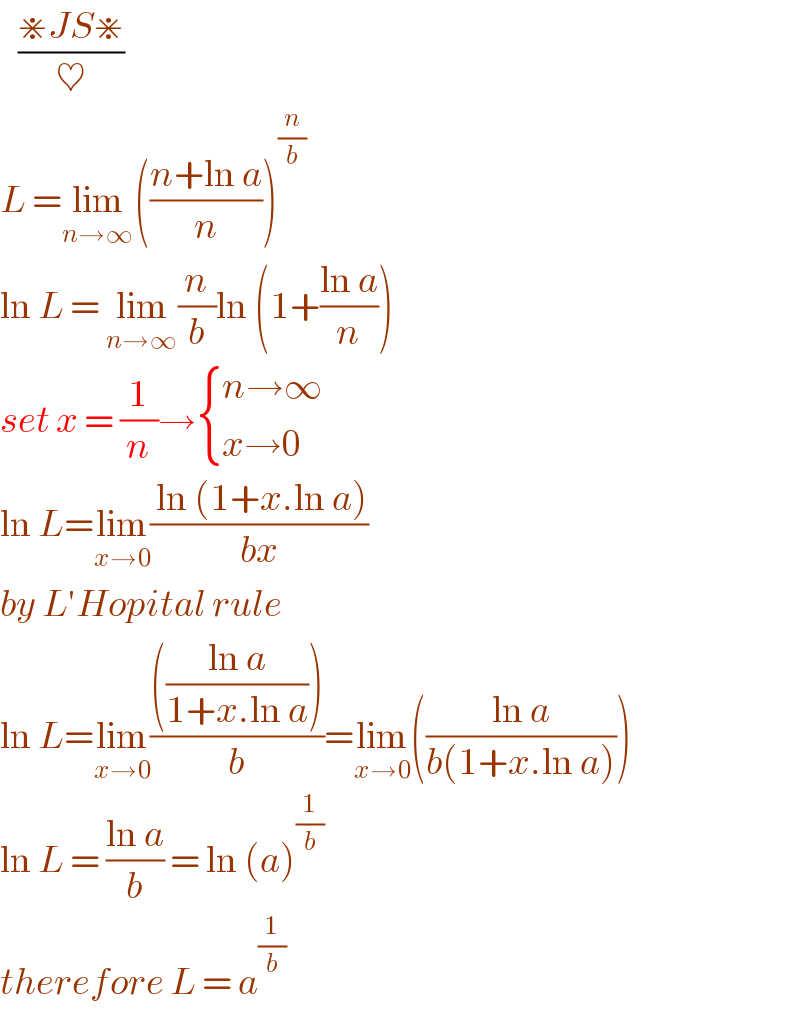
Answered by bemath last updated on 16/Aug/20
![lim_(n→∞) [ (1+(1/(((n/(ln a))))))^(n/(ln a)) ]^((1/b).((ln a)/1)) = e^((ln a)/b) = e^(ln (a)^(1/b) ) = (a)^(1/b) =(a)^(1/b) .](Q108356.png)
| ||
Question and Answers Forum | ||
Question Number 108228 by bemath last updated on 15/Aug/20 | ||
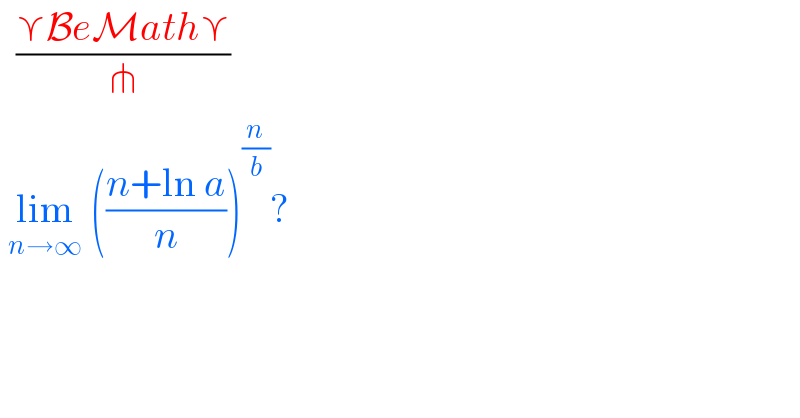 | ||
Answered by Dwaipayan Shikari last updated on 15/Aug/20 | ||
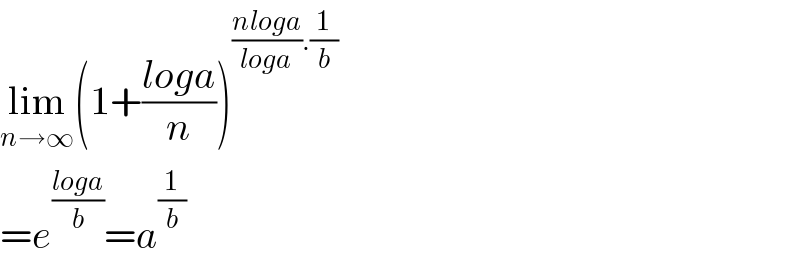 | ||
| ||
Answered by john santu last updated on 15/Aug/20 | ||
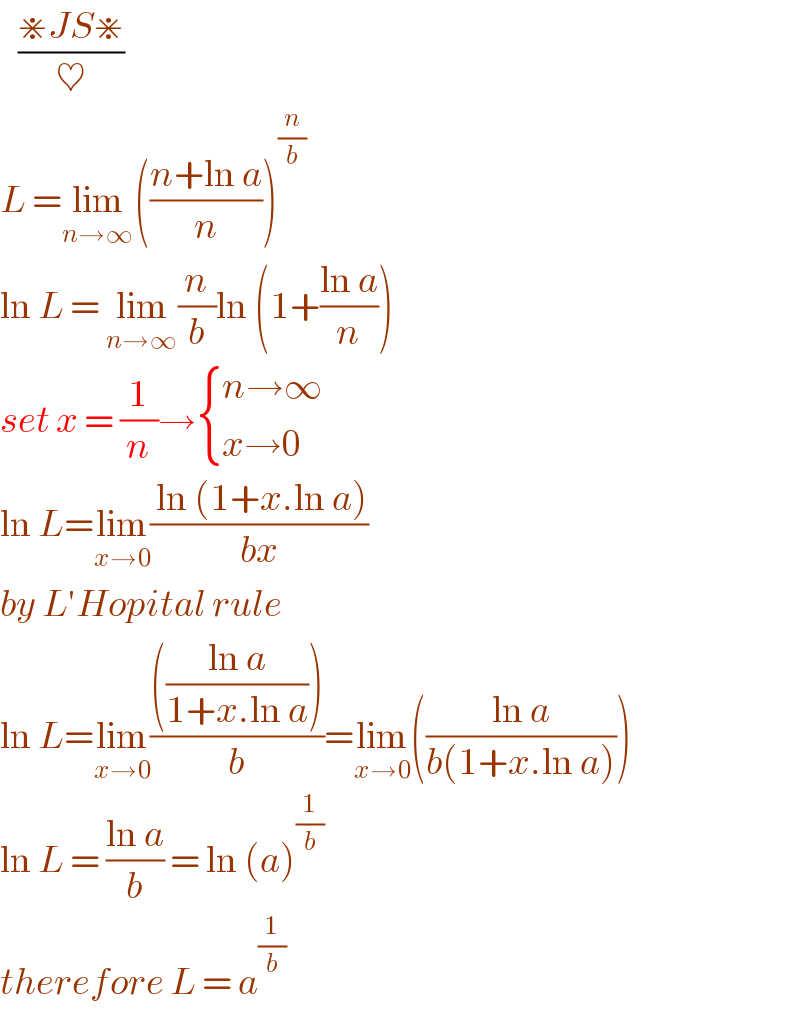 | ||
| ||
Answered by bemath last updated on 16/Aug/20 | ||
![lim_(n→∞) [ (1+(1/(((n/(ln a))))))^(n/(ln a)) ]^((1/b).((ln a)/1)) = e^((ln a)/b) = e^(ln (a)^(1/b) ) = (a)^(1/b) =(a)^(1/b) .](Q108356.png) | ||
| ||