Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 10829 by Saham last updated on 26/Feb/17

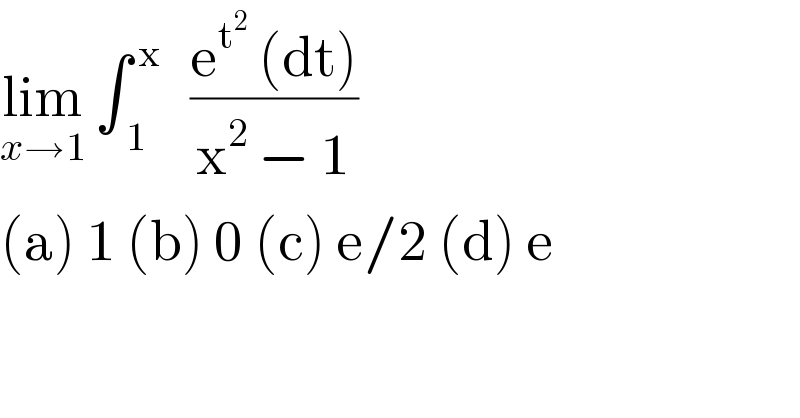
lim_(x→1) ∫_( 1) ^( x) ((e^t^2 (dt))/(x^2 − 1)) (a) 1 (b) 0 (c) e/2 (d) e

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\int_{\:\mathrm{1}} ^{\:\mathrm{x}} \:\:\:\frac{\mathrm{e}^{\mathrm{t}^{\mathrm{2}} } \:\left(\mathrm{dt}\right)}{\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{1}}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{1}\:\left(\mathrm{b}\right)\:\mathrm{0}\:\left(\mathrm{c}\right)\:\mathrm{e}/\mathrm{2}\:\left(\mathrm{d}\right)\:\mathrm{e} \\ $$

Answered by bahmanfeshki last updated on 27/Feb/17

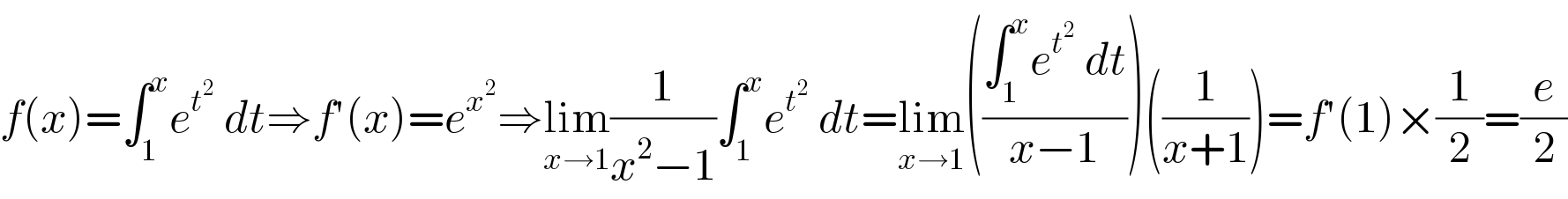
f(x)=∫_1 ^x e^t^2 dt⇒f′(x)=e^x^2 ⇒lim_(x→1) (1/(x^2 −1))∫_1 ^x e^t^2 dt=lim_(x→1) (((∫_1 ^x e^t^2 dt)/(x−1)))((1/(x+1)))=f′(1)×(1/2)=(e/2)

$${f}\left({x}\right)=\int_{\mathrm{1}} ^{{x}} {e}^{{t}^{\mathrm{2}} } \:{dt}\Rightarrow{f}'\left({x}\right)={e}^{{x}^{\mathrm{2}} } \Rightarrow\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{1}} ^{{x}} {e}^{{t}^{\mathrm{2}} } \:{dt}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\int_{\mathrm{1}} ^{{x}} {e}^{{t}^{\mathrm{2}} } \:{dt}}{{x}−\mathrm{1}}\right)\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)={f}'\left(\mathrm{1}\right)×\frac{\mathrm{1}}{\mathrm{2}}=\frac{{e}}{\mathrm{2}} \\ $$

Commented by FilupS last updated on 27/Feb/17

incorrect

$$\mathrm{incorrect} \\ $$

Commented by bahmanfeshki last updated on 27/Feb/17

edited

$${edited} \\ $$

Commented by Saham last updated on 27/Feb/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by FilupS last updated on 27/Feb/17

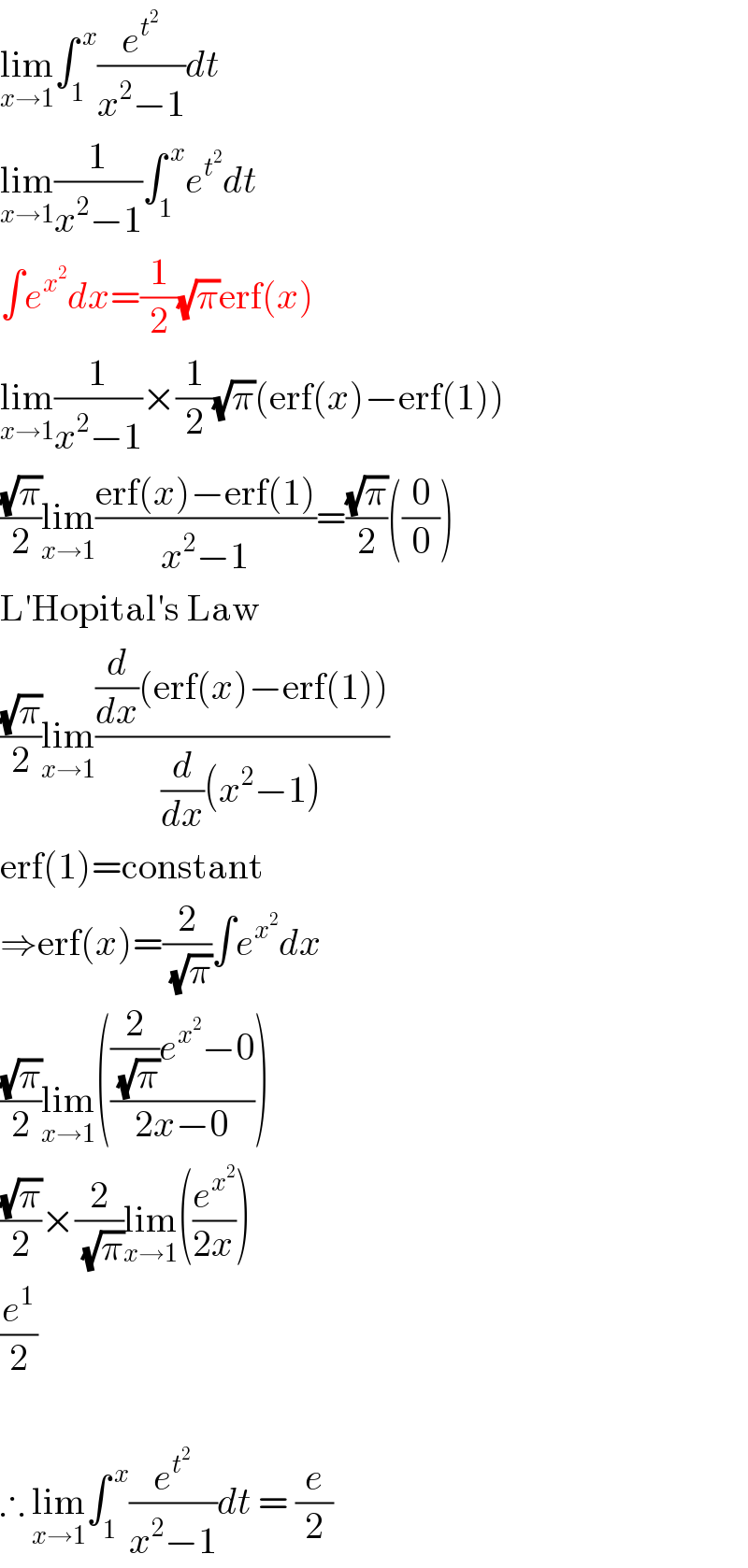
lim_(x→1) ∫_1 ^( x) (e^t^2 /(x^2 −1))dt lim_(x→1) (1/(x^2 −1))∫_1 ^( x) e^t^2 dt ∫e^x^2 dx=(1/2)(√π)erf(x) lim_(x→1) (1/(x^2 −1))×(1/2)(√π)(erf(x)−erf(1)) ((√π)/2)lim_(x→1) ((erf(x)−erf(1))/(x^2 −1))=((√π)/2)((0/0)) L′Hopital′s Law ((√π)/2)lim_(x→1) (((d/dx)(erf(x)−erf(1)))/((d/dx)(x^2 −1))) erf(1)=constant ⇒erf(x)=(2/(√π))∫e^x^2 dx ((√π)/2)lim_(x→1) ((((2/(√π))e^x^2 −0)/(2x−0))) ((√π)/2)×(2/(√π))lim_(x→1) ((e^x^2 /(2x))) (e^1 /2) ∴ lim_(x→1) ∫_1 ^( x) (e^t^2 /(x^2 −1))dt = (e/2)

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\int_{\mathrm{1}} ^{\:{x}} \frac{{e}^{{t}^{\mathrm{2}} } }{{x}^{\mathrm{2}} −\mathrm{1}}{dt} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{1}} ^{\:{x}} {e}^{{t}^{\mathrm{2}} } {dt} \\ $$$$\int{e}^{{x}^{\mathrm{2}} } {dx}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}\mathrm{erf}\left({x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}×\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}\left(\mathrm{erf}\left({x}\right)−\mathrm{erf}\left(\mathrm{1}\right)\right) \\ $$$$\frac{\sqrt{\pi}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{erf}\left({x}\right)−\mathrm{erf}\left(\mathrm{1}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$\mathrm{L}'\mathrm{Hopital}'\mathrm{s}\:\mathrm{Law} \\ $$$$\frac{\sqrt{\pi}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left(\mathrm{erf}\left({x}\right)−\mathrm{erf}\left(\mathrm{1}\right)\right)}{\frac{{d}}{{dx}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\mathrm{erf}\left(\mathrm{1}\right)=\mathrm{constant} \\ $$$$\Rightarrow\mathrm{erf}\left({x}\right)=\frac{\mathrm{2}}{\sqrt{\pi}}\int{e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$\frac{\sqrt{\pi}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\frac{\mathrm{2}}{\sqrt{\pi}}{e}^{{x}^{\mathrm{2}} } −\mathrm{0}}{\mathrm{2}{x}−\mathrm{0}}\right) \\ $$$$\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\mathrm{2}}{\sqrt{\pi}}\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{{e}^{{x}^{\mathrm{2}} } }{\mathrm{2}{x}}\right) \\ $$$$\frac{{e}^{\mathrm{1}} }{\mathrm{2}} \\ $$$$\: \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\int_{\mathrm{1}} ^{\:{x}} \frac{{e}^{{t}^{\mathrm{2}} } }{{x}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\:\frac{{e}}{\mathrm{2}} \\ $$

Commented by Saham last updated on 27/Feb/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by bahmanfeshki last updated on 27/Feb/17

my answer is edited...

$${my}\:{answer}\:{is}\:{edited}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com