Question Number 108391 by bemath last updated on 16/Aug/20
$$\:\:\:\frac{\measuredangle\:\mathcal{B}{e}\mathcal{M}{ath}\:\measuredangle}{\bigtriangledown} \\ $$$${I}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{{x}\:{dx}}{\mathrm{1}+\mathrm{sin}\:{x}} \\ $$
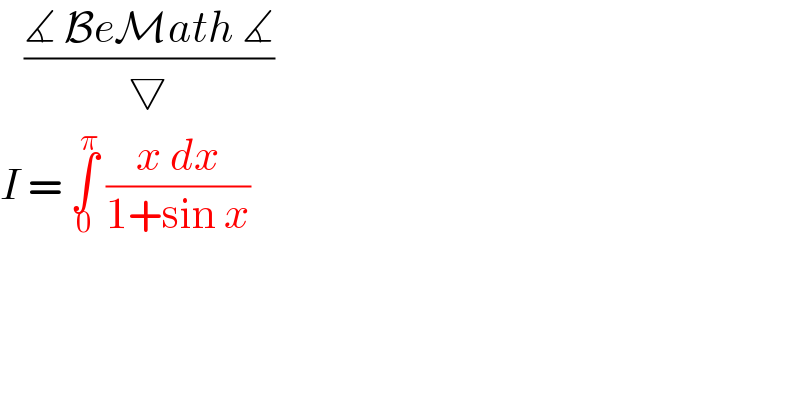
Answered by bobhans last updated on 16/Aug/20
Commented by khanshadab2405 last updated on 16/Aug/20
1/√1²+cot²∅
Commented by bobhans last updated on 16/Aug/20
$${typo}\:{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{−\pi/\mathrm{4}} {\overset{\pi/\mathrm{4}} {\int}}\left(\mathrm{4}{w}+\pi\right)\mathrm{sec}\:^{\mathrm{2}} {w}\:{dw}\: \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\pi\:=\:\pi\: \\ $$
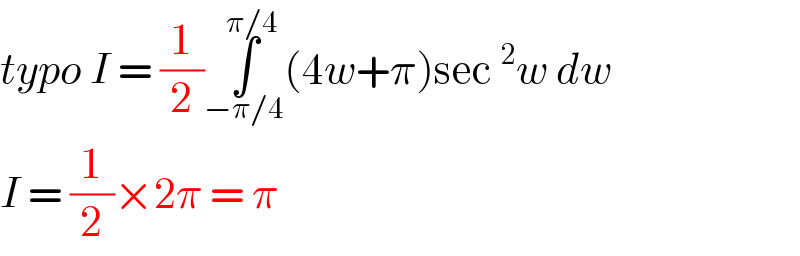
Answered by Dwaipayan Shikari last updated on 16/Aug/20
![∫_0 ^π ((xdx)/(1+sinx))=∫_0 ^π ((π−x)/(1+sinx))dx=I 2I=∫_0 ^π (π/(1+sinx))dx 2I=2π∫_0 ^∞ (1/(1+((2t)/(1+t^2 )))).(1/(1+t^2 ))dt (tan(x/2)=t 2I=2π∫_0 ^∞ (1/((1+t)^2 )) I=π[−(1/(1+t))]_0 ^∞ I=π](Q108396.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{{xdx}}{\mathrm{1}+{sinx}}=\int_{\mathrm{0}} ^{\pi} \frac{\pi−{x}}{\mathrm{1}+{sinx}}{dx}={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{1}+{sinx}}{dx} \\ $$$$\mathrm{2}{I}=\mathrm{2}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\:\:\:\:\:\left({tan}\frac{{x}}{\mathrm{2}}={t}\right. \\ $$$$\mathrm{2}{I}=\mathrm{2}\pi\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} } \\ $$$${I}=\pi\left[−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right]_{\mathrm{0}} ^{\infty} \\ $$$${I}=\pi \\ $$
Answered by mnjuly1970 last updated on 16/Aug/20
![I=∫_0 ^( π) (((π−x)dx)/(1+sin(π−x)))dx ⇒2I=π∫_0 ^( π) ((1−sin(x))/(cos^2 (x)))dx 2I=π([tan(x)]_0 ^π −[(1/(cos(x)))]_0 ^( π) )=π(2) I=π ♣...........♣](Q108398.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\pi} \frac{\left(\pi−{x}\right){dx}}{\mathrm{1}+{sin}\left(\pi−{x}\right)}{dx} \\ $$$$\Rightarrow\mathrm{2I}=\pi\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{1}−{sin}\left({x}\right)}{{cos}^{\mathrm{2}} \left({x}\right)}{dx} \\ $$$$\mathrm{2I}=\pi\left(\left[{tan}\left({x}\right)\right]_{\mathrm{0}} ^{\pi} −\left[\frac{\mathrm{1}}{{cos}\left({x}\right)}\right]_{\mathrm{0}} ^{\:\pi} \right)=\pi\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\mathrm{I}=\pi\:\:\:\clubsuit...........\clubsuit \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 16/Aug/20
![I =∫_0 ^π ((xdx)/(1+sinx)) changement x=π−t give I =∫_0 ^π (((π−t))/(1+sint))dt =π ∫_0 ^π (dt/(1+sint))−I ⇒2I =π∫_0 ^π (dt/(1+sint)) =_(tan((t/2))=u) π ∫_0 ^∞ ((2du)/((1+u^2 )(1+((2u)/(1+u^2 ))))) =2π ∫_0 ^∞ (du/(1+u^2 +2u)) =2π ∫_0 ^∞ (du/((u+1)^2 )) =2π[−(1/(u+1))]_0 ^(+∞) =2π ⇒ 2I =2π ⇒ I =π](Q108405.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{sinx}}\:\:\mathrm{changement}\:\mathrm{x}=\pi−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\left(\pi−\mathrm{t}\right)}{\mathrm{1}+\mathrm{sint}}\mathrm{dt}\:=\pi\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sint}}−\mathrm{I}\:\Rightarrow\mathrm{2I}\:=\pi\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{sint}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \:\:\:\pi\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)} \\ $$$$=\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} \:+\mathrm{2u}}\:=\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{du}}{\left(\mathrm{u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{2}\pi\left[−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\right]_{\mathrm{0}} ^{+\infty} \:=\mathrm{2}\pi\:\Rightarrow \\ $$$$\mathrm{2I}\:=\mathrm{2}\pi\:\Rightarrow\:\mathrm{I}\:=\pi \\ $$
Answered by mathmax by abdo last updated on 16/Aug/20
![another way changement tan((x/2))=t give I =∫_0 ^∞ ((2arctan(t))/((1+((2t)/(1+t^2 )))))((2dt)/(1+t^2 )) =4∫_0 ^∞ ((arctant)/(1+t^2 +2t))dt =4∫_0 ^∞ ((arctant)/((t+1)^2 ))dt =_(byparts) 4{[−((arctant)/(t+1))]_0 ^(+∞) +∫_0 ^∞ (1/(t+1))(dt/(1+t^2 ))} =4 ∫_0 ^∞ (dt/((t+1)(t^2 +1))) let decompose F(t) =(1/((t+1)(t^2 +1))) F(t) =(a/(t+1)) +((bt +c)/(t^2 +1)) a =(1/2) , lim_(t→+∞) tF(t) =0 =a+b ⇒b=−(1/2) F(0) =1 =a +c ⇒c=1−a =(1/2) ⇒F(t)=(1/(2(t+1)))+((−(1/2)t +(1/2))/(t^2 +1)) ⇒ ∫_0 ^∞ F(t)dt =(1/2)∫_0 ^∞ (dt/(t+1))−(1/4)∫_0 ^∞ ((2t)/(t^2 +1)) +(1/2)∫_0 ^∞ (dt/(1+t^2 )) =[(1/2)ln(t+1)−(1/4)ln(t^2 +1)]_0 ^∞ +(1/2)[arctant]_0 ^∞ =[ln(((√(t+1))/((^4 (√(t^2 +1))))))]_0 ^(+∞) +(1/2){(π/2)} =(π/4) ⇒I =4.(π/4) ⇒I =π](Q108408.png)
$$\mathrm{another}\:\mathrm{way}\:\:\mathrm{changement}\:\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2arctan}\left(\mathrm{t}\right)}{\left(\mathrm{1}+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{arctant}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} \:+\mathrm{2t}}\mathrm{dt} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctant}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{byparts}} \:\:\:\mathrm{4}\left\{\left[−\frac{\mathrm{arctant}}{\mathrm{t}+\mathrm{1}}\right]_{\mathrm{0}} ^{+\infty} +\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right\} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{t}\right)\:=\frac{\mathrm{a}}{\mathrm{t}+\mathrm{1}}\:+\frac{\mathrm{bt}\:+\mathrm{c}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:,\:\:\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{tF}\left(\mathrm{t}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\mathrm{a}\:+\mathrm{c}\:\Rightarrow\mathrm{c}=\mathrm{1}−\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)}+\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}\:+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\infty} \:+\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{arctant}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\left[\mathrm{ln}\left(\frac{\sqrt{\mathrm{t}+\mathrm{1}}}{\left(^{\mathrm{4}} \sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\right)}\right)\right]_{\mathrm{0}} ^{+\infty} \:+\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\pi}{\mathrm{2}}\right\}\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow\mathrm{I}\:=\mathrm{4}.\frac{\pi}{\mathrm{4}}\:\Rightarrow\mathrm{I}\:=\pi \\ $$