Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 108597 by bemath last updated on 18/Aug/20

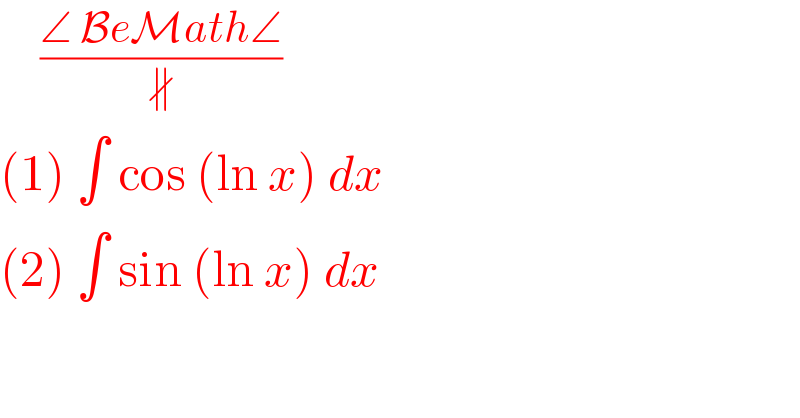
((∠ BeMath∠)/∦) (1) ∫ cos (ln x) dx (2) ∫ sin (ln x) dx

$$\:\:\:\:\:\frac{\angle\:\mathcal{B}{e}\mathcal{M}{ath}\angle}{\nparallel} \\ $$$$\left(\mathrm{1}\right)\:\int\:\mathrm{cos}\:\left(\mathrm{ln}\:{x}\right)\:{dx}\: \\ $$$$\left(\mathrm{2}\right)\:\int\:\mathrm{sin}\:\left(\mathrm{ln}\:{x}\right)\:{dx}\: \\ $$

Answered by 1549442205PVT last updated on 18/Aug/20

Set I=∫cos(lnx)dx,J=∫sin(lnx)dx By integrating by parts we have I=xcos(lnx)−∫x.(−sin(lnx)).(1/x)dx =xcos(lnx)+J⇒I−J=xcos(lnx)(1) J=∫sin(lnx)dx=xsin(lnx)−∫x.cos(lnx).(1/x)dx =xsin(lnx)−J⇒I+J=xsin(lnx)(2) Solve the system of equations (1)(2) we get { ((I=∫cos(lnx)dx=((x[(cos(lnx)+sin(lnx)])/2)+C)),((J=∫sin(lnx)dx=((x[sin(lnx)−cos(lnx)])/2)+C )) :}

$$\mathrm{Set}\:\mathrm{I}=\int\mathrm{cos}\left(\mathrm{lnx}\right)\mathrm{dx},\mathrm{J}=\int\mathrm{sin}\left(\mathrm{lnx}\right)\mathrm{dx} \\ $$$$\mathrm{By}\:\mathrm{integrating}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{I}=\mathrm{xcos}\left(\mathrm{lnx}\right)−\int\mathrm{x}.\left(−\mathrm{sin}\left(\mathrm{lnx}\right)\right).\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{xcos}\left(\mathrm{lnx}\right)+\mathrm{J}\Rightarrow\mathrm{I}−\mathrm{J}=\mathrm{xcos}\left(\mathrm{lnx}\right)\left(\mathrm{1}\right) \\ $$$$\mathrm{J}=\int\mathrm{sin}\left(\mathrm{lnx}\right)\mathrm{dx}=\mathrm{xsin}\left(\mathrm{lnx}\right)−\int\mathrm{x}.\mathrm{cos}\left(\mathrm{lnx}\right).\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{xsin}\left(\mathrm{lnx}\right)−\mathrm{J}\Rightarrow\mathrm{I}+\mathrm{J}=\mathrm{xsin}\left(\mathrm{lnx}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{\boldsymbol{\mathrm{I}}=\int\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{lnx}}\right)\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{x}}\left[\left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{lnx}}\right)+\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{lnx}}\right)\right]\right.}{\mathrm{2}}+\mathrm{C}}\\{\boldsymbol{\mathrm{J}}=\int\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{lnx}}\right)\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{x}}\left[\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{lnx}}\right)−\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{lnx}}\right)\right]}{\mathrm{2}}+\mathrm{C}\:}\end{cases} \\ $$

Commented by bemath last updated on 18/Aug/20

jooss....

$${jooss}.... \\ $$

Answered by bemath last updated on 18/Aug/20

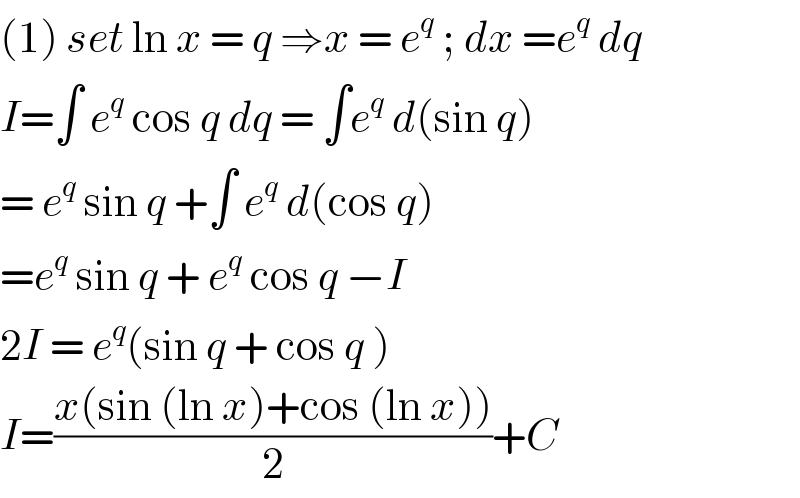
(1) set ln x = q ⇒x = e^q ; dx =e^q dq I=∫ e^q cos q dq = ∫e^q d(sin q) = e^q sin q +∫ e^q d(cos q) =e^q sin q + e^q cos q −I 2I = e^q (sin q + cos q ) I=((x(sin (ln x)+cos (ln x)))/2)+C

$$\left(\mathrm{1}\right)\:{set}\:\mathrm{ln}\:{x}\:=\:{q}\:\Rightarrow{x}\:=\:{e}^{{q}} \:;\:{dx}\:={e}^{{q}} \:{dq} \\ $$$${I}=\int\:{e}^{{q}} \:\mathrm{cos}\:{q}\:{dq}\:=\:\int{e}^{{q}} \:{d}\left(\mathrm{sin}\:{q}\right) \\ $$$$=\:{e}^{{q}} \:\mathrm{sin}\:{q}\:+\int\:{e}^{{q}} \:{d}\left(\mathrm{cos}\:{q}\right)\: \\ $$$$={e}^{{q}} \:\mathrm{sin}\:{q}\:+\:{e}^{{q}} \:\mathrm{cos}\:{q}\:−{I} \\ $$$$\mathrm{2}{I}\:=\:{e}^{{q}} \left(\mathrm{sin}\:{q}\:+\:\mathrm{cos}\:{q}\:\right) \\ $$$${I}=\frac{{x}\left(\mathrm{sin}\:\left(\mathrm{ln}\:{x}\right)+\mathrm{cos}\:\left(\mathrm{ln}\:{x}\right)\right)}{\mathrm{2}}+{C} \\ $$

Answered by mathmax by abdo last updated on 18/Aug/20

1) I =∫ cos(lnx)dx changement lnx =t give x=e^t ⇒ I =∫ cost e^t dt =∫ e^t cost =_(byparts) e^t sint −∫ e^t sint dt =e^t sint −{ −e^t cost +∫ e^t cost dt} =e^t sint +e^t cost −I+c ⇒2I =(cost +sint)e^t +c ⇒I =(1/2)(cost +sint)e^t +C =(x/2)(cos(lnx)+sin(lnx)) +C

$$\left.\mathrm{1}\right)\:\mathrm{I}\:=\int\:\mathrm{cos}\left(\mathrm{lnx}\right)\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{x}=\mathrm{e}^{\mathrm{t}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\mathrm{cost}\:\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}\:=\int\:\mathrm{e}^{\mathrm{t}} \:\mathrm{cost}\:=_{\mathrm{byparts}} \:\:\mathrm{e}^{\mathrm{t}} \mathrm{sint}\:−\int\:\mathrm{e}^{\mathrm{t}} \:\mathrm{sint}\:\mathrm{dt} \\ $$$$=\mathrm{e}^{\mathrm{t}} \:\mathrm{sint}\:−\left\{\:\:−\mathrm{e}^{\mathrm{t}} \mathrm{cost}\:+\int\:\mathrm{e}^{\mathrm{t}} \mathrm{cost}\:\mathrm{dt}\right\} \\ $$$$=\mathrm{e}^{\mathrm{t}} \mathrm{sint}\:\:+\mathrm{e}^{\mathrm{t}} \:\mathrm{cost}\:−\mathrm{I}+\mathrm{c}\:\Rightarrow\mathrm{2I}\:=\left(\mathrm{cost}\:+\mathrm{sint}\right)\mathrm{e}^{\mathrm{t}} +\mathrm{c}\:\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cost}\:+\mathrm{sint}\right)\mathrm{e}^{\mathrm{t}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{cos}\left(\mathrm{lnx}\right)+\mathrm{sin}\left(\mathrm{lnx}\right)\right)\:+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com