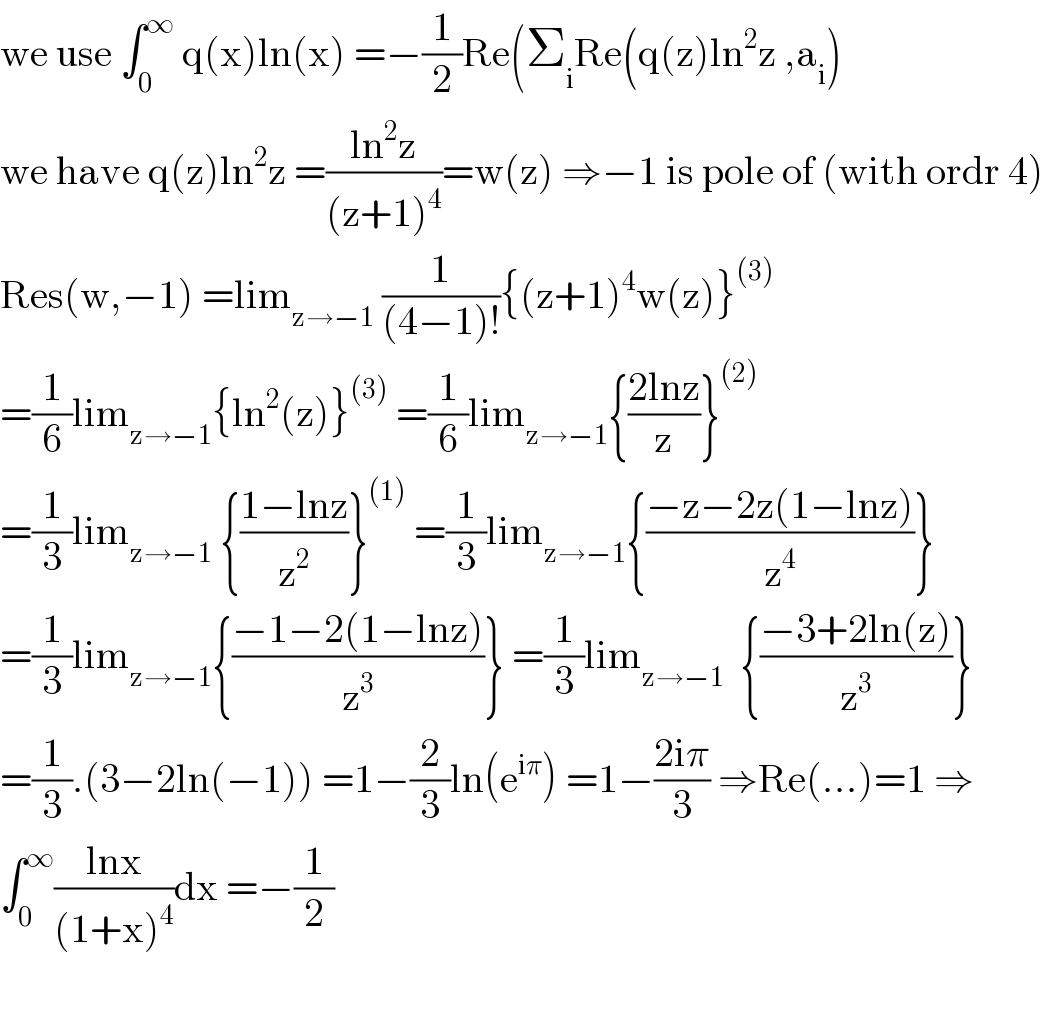Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 108749 by mathmax by abdo last updated on 19/Aug/20

calculste ∫_0 ^∞ ((ln(x))/((1+x)^4 )) dx

$$\mathrm{calculste}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{4}} }\:\mathrm{dx} \\ $$

Answered by mnjuly1970 last updated on 19/Aug/20

f(a)=∫_0 ^( ∞) (x^a /((1+x)^4 ))⇒goal:=f^( ′) (0) f^( ′) (a)=(d/da)[β(a+1,3−a)]=(1/6)(d/da)[Γ(a+1).Γ(3−a)] =(1/6) [Γ^( ′) (1).Γ(3)−Γ^( ′) (3)Γ(1)] =(1/6)[−2γ−2ψ(3)]=(1/6)[−2γ−2((3/2) − γ)] ((−1)/2) ....

$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{a}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{4}} }\Rightarrow\mathrm{goal}:={f}^{\:'} \left(\mathrm{0}\right) \\ $$$${f}^{\:'} \left({a}\right)=\frac{{d}}{{da}}\left[\beta\left({a}+\mathrm{1},\mathrm{3}−{a}\right)\right]=\frac{\mathrm{1}}{\mathrm{6}}\frac{{d}}{{da}}\left[\Gamma\left({a}+\mathrm{1}\right).\Gamma\left(\mathrm{3}−{a}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\:\left[\Gamma^{\:'} \left(\mathrm{1}\right).\Gamma\left(\mathrm{3}\right)−\Gamma^{\:'} \left(\mathrm{3}\right)\Gamma\left(\mathrm{1}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[−\mathrm{2}\gamma−\mathrm{2}\psi\left(\mathrm{3}\right)\right]=\frac{\mathrm{1}}{\mathrm{6}}\left[−\mathrm{2}\gamma−\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}\:−\:\gamma\right)\right] \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\:.... \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 19/Aug/20

thankx sir

$$\mathrm{thankx}\:\mathrm{sir} \\ $$

Commented by mnjuly1970 last updated on 19/Aug/20

thank you master..yourquestions are very nice...

$${thank}\:{you}\:{master}..{yourquestions} \\ $$$${are}\:{very}\:{nice}... \\ $$

Answered by mathmax by abdo last updated on 19/Aug/20

we use ∫_0 ^∞ q(x)ln(x) =−(1/2)Re(Σ_i Re(q(z)ln^2 z ,a_i ) we have q(z)ln^2 z =((ln^2 z)/((z+1)^4 ))=w(z) ⇒−1 is pole of (with ordr 4) Res(w,−1) =lim_(z→−1) (1/((4−1)!)){(z+1)^4 w(z)}^((3)) =(1/6)lim_(z→−1) {ln^2 (z)}^((3)) =(1/6)lim_(z→−1) {((2lnz)/z)}^((2)) =(1/3)lim_(z→−1) {((1−lnz)/z^2 )}^((1)) =(1/3)lim_(z→−1) {((−z−2z(1−lnz))/z^4 )} =(1/3)lim_(z→−1) {((−1−2(1−lnz))/z^3 )} =(1/3)lim_(z→−1) {((−3+2ln(z))/z^3 )} =(1/3).(3−2ln(−1)) =1−(2/3)ln(e^(iπ) ) =1−((2iπ)/3) ⇒Re(...)=1 ⇒ ∫_0 ^∞ ((lnx)/((1+x)^4 ))dx =−(1/2)

$$\mathrm{we}\:\mathrm{use}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{q}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\sum_{\mathrm{i}} \mathrm{Re}\left(\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:,\mathrm{a}_{\mathrm{i}} \right)\:\:\right. \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{4}} }=\mathrm{w}\left(\mathrm{z}\right)\:\Rightarrow−\mathrm{1}\:\mathrm{is}\:\mathrm{pole}\:\mathrm{of}\:\left(\mathrm{with}\:\mathrm{ordr}\:\mathrm{4}\right) \\ $$$$\mathrm{Res}\left(\mathrm{w},−\mathrm{1}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\frac{\mathrm{1}}{\left(\mathrm{4}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{4}} \mathrm{w}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}\right)\right\}^{\left(\mathrm{3}\right)} \:=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\frac{\mathrm{2lnz}}{\mathrm{z}}\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\left\{\frac{\mathrm{1}−\mathrm{lnz}}{\mathrm{z}^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\frac{−\mathrm{z}−\mathrm{2z}\left(\mathrm{1}−\mathrm{lnz}\right)}{\mathrm{z}^{\mathrm{4}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\frac{−\mathrm{1}−\mathrm{2}\left(\mathrm{1}−\mathrm{lnz}\right)}{\mathrm{z}^{\mathrm{3}} }\right\}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\:\left\{\frac{−\mathrm{3}+\mathrm{2ln}\left(\mathrm{z}\right)}{\mathrm{z}^{\mathrm{3}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}.\left(\mathrm{3}−\mathrm{2ln}\left(−\mathrm{1}\right)\right)\:=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{e}^{\mathrm{i}\pi} \right)\:=\mathrm{1}−\frac{\mathrm{2i}\pi}{\mathrm{3}}\:\Rightarrow\mathrm{Re}\left(...\right)=\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{4}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com