Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 108842 by Study last updated on 19/Aug/20

Commented by Study last updated on 19/Aug/20

i need u help

$${i}\:{need}\:{u}\:{help} \\ $$

Commented by 150505R last updated on 19/Aug/20

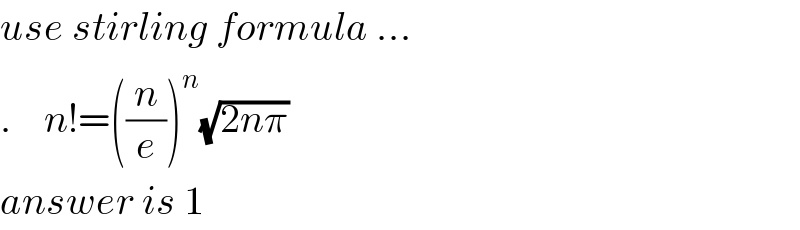
use stirling formula ... . n!=((n/e))^n (√(2nπ)) answer is 1

$${use}\:{stirling}\:{formula}\:... \\ $$$$.\:\:\:\:{n}!=\left(\frac{{n}}{{e}}\right)^{{n}} \sqrt{\mathrm{2}{n}\pi} \\ $$$${answer}\:{is}\:\mathrm{1} \\ $$

Commented by Study last updated on 19/Aug/20

=??????????

$$=?????????? \\ $$

Answered by Dwaipayan Shikari last updated on 19/Aug/20

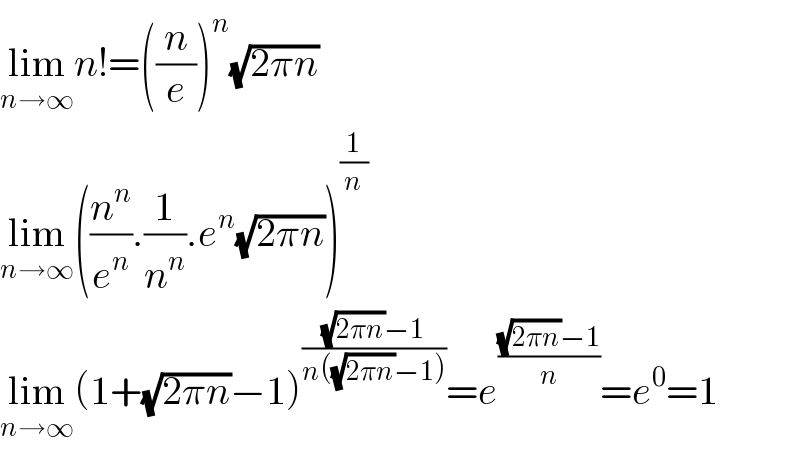
lim_(n→∞) n!=((n/e))^n (√(2πn)) lim_(n→∞) ((n^n /e^n ).(1/n^n ).e^n (√(2πn)))^(1/n) lim_(n→∞) (1+(√(2πn))−1)^(((√(2πn))−1)/(n((√(2πn))−1))) =e^(((√(2πn))−1)/n) =e^0 =1

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}!=\left(\frac{{n}}{{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}^{{n}} }{{e}^{{n}} }.\frac{\mathrm{1}}{{n}^{{n}} }.{e}^{{n}} \sqrt{\mathrm{2}\pi{n}}\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\sqrt{\mathrm{2}\pi{n}}−\mathrm{1}\right)^{\frac{\sqrt{\mathrm{2}\pi{n}}−\mathrm{1}}{{n}\left(\sqrt{\mathrm{2}\pi{n}}−\mathrm{1}\right)}} ={e}^{\frac{\sqrt{\mathrm{2}\pi{n}}−\mathrm{1}}{{n}}} ={e}^{\mathrm{0}} =\mathrm{1} \\ $$

Commented by Study last updated on 19/Aug/20

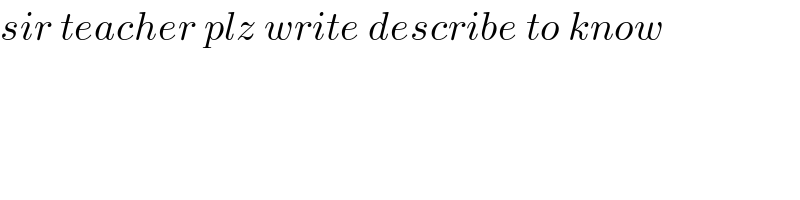
sir teacher plz write describe to know

$${sir}\:{teacher}\:{plz}\:{write}\:{describe}\:{to}\:{know} \\ $$

Commented by Dwaipayan Shikari last updated on 19/Aug/20

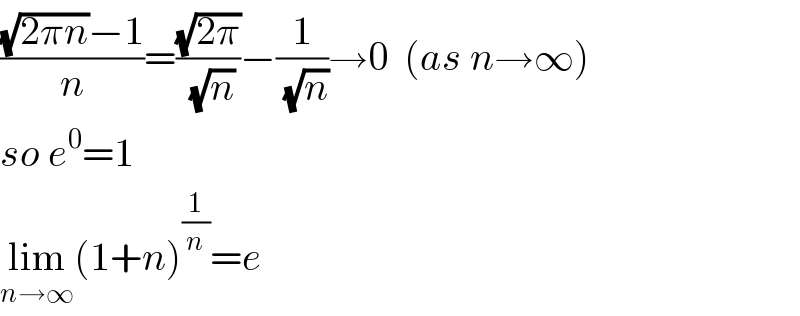
(((√(2πn))−1)/n)=((√(2π))/( (√n)))−(1/( (√n)))→0 (as n→∞) so e^0 =1 lim_(n→∞) (1+n)^(1/n) =e

$$\frac{\sqrt{\mathrm{2}\pi{n}}−\mathrm{1}}{{n}}=\frac{\sqrt{\mathrm{2}\pi}}{\:\sqrt{{n}}}−\frac{\mathrm{1}}{\:\sqrt{{n}}}\rightarrow\mathrm{0}\:\:\left({as}\:{n}\rightarrow\infty\right) \\ $$$${so}\:{e}^{\mathrm{0}} =\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+{n}\right)^{\frac{\mathrm{1}}{{n}}} ={e} \\ $$

Answered by Dwaipayan Shikari last updated on 19/Aug/20

Another way lim_(n→∞) (((n!)/n^n ))^(1/n) e=y (1/n)(log(1)+log(1−(1/n))+....+(log(1−(n/n)))+1=logy (1/n)Σ_(r=1) ^n log(1−(r/n))+1=logy ∫_0 ^1 log(1−x)dx+1=logy xlog(1−x)−∫(x/(1−x))+1=logy [xlog(1−x)−x+logx]_0 ^1 +1=logy logy=−1+1 y=1

$${Another}\:{way} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}!}{{n}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} {e}={y} \\ $$$$\frac{\mathrm{1}}{{n}}\left({log}\left(\mathrm{1}\right)+{log}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)+....+\left({log}\left(\mathrm{1}−\frac{{n}}{{n}}\right)\right)+\mathrm{1}={logy}\right. \\ $$$$\frac{\mathrm{1}}{{n}}\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{log}\left(\mathrm{1}−\frac{{r}}{{n}}\right)+\mathrm{1}={logy} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\mathrm{1}−{x}\right){dx}+\mathrm{1}={logy} \\ $$$${xlog}\left(\mathrm{1}−{x}\right)−\int\frac{{x}}{\mathrm{1}−{x}}+\mathrm{1}={logy} \\ $$$$\left[{xlog}\left(\mathrm{1}−{x}\right)−{x}+{logx}\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{1}={logy} \\ $$$${logy}=−\mathrm{1}+\mathrm{1} \\ $$$${y}=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com