Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 108888 by bemath last updated on 20/Aug/20

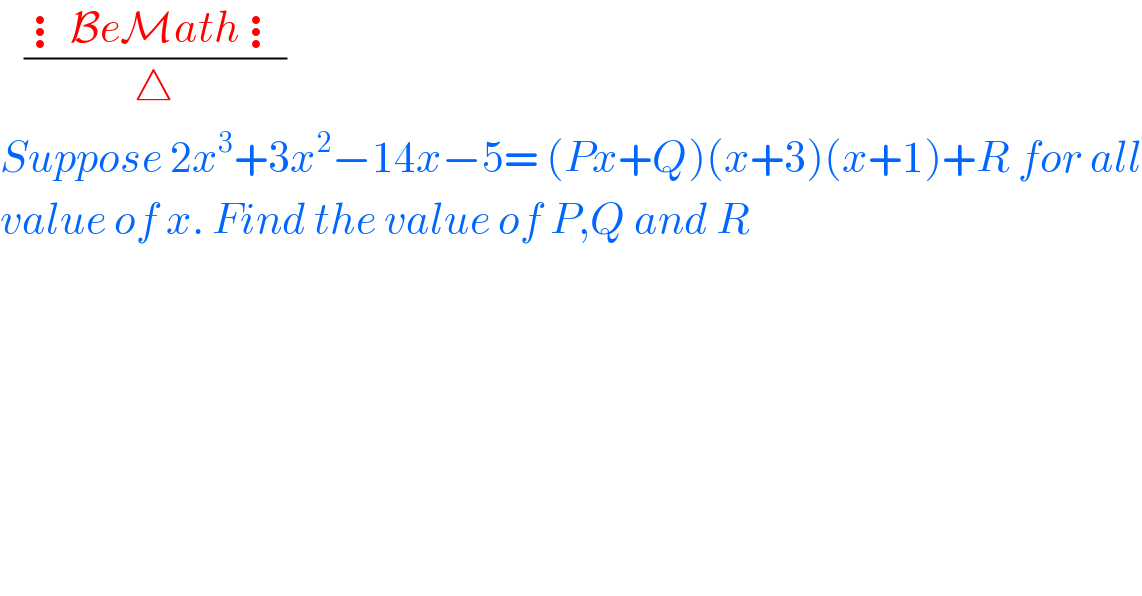
((⋮BeMath⋮)/△) Suppose 2x^3 +3x^2 −14x−5= (Px+Q)(x+3)(x+1)+R for all value of x. Find the value of P,Q and R

$$\:\:\:\frac{\vdots\mathcal{B}{e}\mathcal{M}{ath}\vdots}{\bigtriangleup} \\ $$$${Suppose}\:\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{14}{x}−\mathrm{5}=\:\left({Px}+{Q}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)+{R}\:{for}\:{all} \\ $$$${value}\:{of}\:{x}.\:{Find}\:{the}\:{value}\:{of}\:{P},{Q}\:{and}\:{R}\: \\ $$

Answered by Rasheed.Sindhi last updated on 20/Aug/20

⟩_• ^• ∣_• ^• ⟨_• ^• Comparing Coefficients 2x^3 +3x^2 −14x−5 = (Px+Q)(x+3)(x+1)+R =Px^3 +(4P+Q)x^2 +(3P+4Q)x+3Q+R Comparing coefficients: P=2, 4P+Q=3,3P+4Q=−14 3Q+R=−5 Q=3−4P=3−4(2)=−5 Q=−5,R=−5−3Q=−5−3(−5) R=10 _(⋘• )^(⋙ •) Rasheed_( •⋘) ^( •⋙)

$$\:\underset{\bullet} {\overset{\bullet} {\rangle}}\underset{\bullet} {\overset{\bullet} {\mid}}\underset{\bullet} {\overset{\bullet} {\langle}}\:\mathrm{Comparing}\:\mathrm{Coefficients}\:\: \\ $$$$\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{14}{x}−\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:=\:\left({Px}+{Q}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)+{R}\: \\ $$$$\:\:\:\:\:\:\:\:={Px}^{\mathrm{3}} +\left(\mathrm{4}{P}+{Q}\right){x}^{\mathrm{2}} +\left(\mathrm{3}{P}+\mathrm{4}{Q}\right){x}+\mathrm{3}{Q}+{R} \\ $$$${Comparing}\:{coefficients}: \\ $$$${P}=\mathrm{2},\:\mathrm{4}{P}+\mathrm{Q}=\mathrm{3},\mathrm{3}{P}+\mathrm{4}{Q}=−\mathrm{14} \\ $$$$\mathrm{3}{Q}+{R}=−\mathrm{5} \\ $$$${Q}=\mathrm{3}−\mathrm{4}{P}=\mathrm{3}−\mathrm{4}\left(\mathrm{2}\right)=−\mathrm{5} \\ $$$${Q}=−\mathrm{5},{R}=−\mathrm{5}−\mathrm{3}{Q}=−\mathrm{5}−\mathrm{3}\left(−\mathrm{5}\right) \\ $$$${R}=\mathrm{10}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:_{\lll\bullet\:} ^{\ggg\:\bullet} {Rasheed}_{\:\bullet\lll} ^{\:\:\bullet\ggg} \\ $$

Commented by bemath last updated on 20/Aug/20

cooll ...nice

$${cooll}\:...{nice} \\ $$

Answered by bobhans last updated on 20/Aug/20

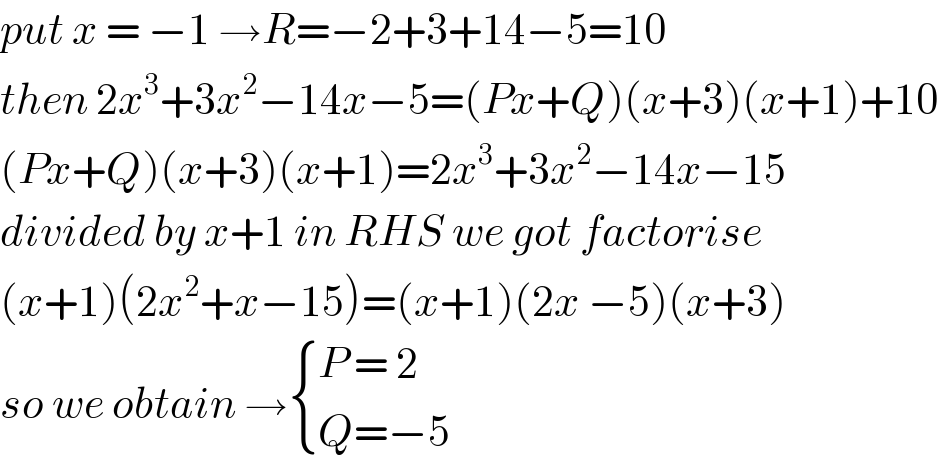
put x = −1 →R=−2+3+14−5=10 then 2x^3 +3x^2 −14x−5=(Px+Q)(x+3)(x+1)+10 (Px+Q)(x+3)(x+1)=2x^3 +3x^2 −14x−15 divided by x+1 in RHS we got factorise (x+1)(2x^2 +x−15)=(x+1)(2x −5)(x+3) so we obtain → { ((P = 2)),((Q=−5)) :}

$${put}\:{x}\:=\:−\mathrm{1}\:\rightarrow{R}=−\mathrm{2}+\mathrm{3}+\mathrm{14}−\mathrm{5}=\mathrm{10} \\ $$$${then}\:\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{14}{x}−\mathrm{5}=\left({Px}+{Q}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)+\mathrm{10} \\ $$$$\left({Px}+{Q}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)=\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{14}{x}−\mathrm{15} \\ $$$${divided}\:{by}\:{x}+\mathrm{1}\:{in}\:{RHS}\:{we}\:{got}\:{factorise} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{15}\right)=\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}\:−\mathrm{5}\right)\left({x}+\mathrm{3}\right) \\ $$$${so}\:{we}\:{obtain}\:\rightarrow\begin{cases}{{P}\:=\:\mathrm{2}}\\{{Q}=−\mathrm{5}}\end{cases} \\ $$

Commented by bemath last updated on 20/Aug/20

cooll...★

$${cooll}...\bigstar \\ $$

Answered by Rasheed.Sindhi last updated on 20/Aug/20

S_(⊂) ^(∩) yntheic Division method_∪ ^⊃ g(x):2x^3 +3x^2 −14x−5 = (Px+Q)(x+3)(x+1)+R g(x) on dividing by x+1 gives remainder R and quotient q(x): determinant (((−1)),2,( 3),(−14),(−5)),(,,(−2),( −1),( 15)),(,2,( 1),(−15),( 10^(R=) ))) q(x)=2x^2 +x−15 , R=10 q(x) on dividing by x+3 gives remainder 0 and quotient Px+Q determinant (((−3)),2,( 1),(−15)),(,,(−6),(+15)),(,2^(P=) ,(−5^(Q=) ),( 0))) Px+Q=2x−5 P=2, Q=−5

$$\:\:\:\:\:\underset{\subset} {\overset{\cap} {\mathrm{S}}yntheic}\:\mathrm{Division}\:\mathrm{metho}\underset{\cup} {\overset{\supset} {\mathrm{d}}} \\ $$$$\:{g}\left({x}\right):\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{14}{x}−\mathrm{5} \\ $$$$\:\:\:\:\:\:=\:\left({Px}+{Q}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)+{R} \\ $$$${g}\left({x}\right)\:{on}\:{dividing}\:{by}\:{x}+\mathrm{1}\:{gives}\: \\ $$$${remainder}\:{R}\:{and}\:{quotient}\:{q}\left({x}\right): \\ $$$$\begin{vmatrix}{\left.−\mathrm{1}\right)}&{\mathrm{2}}&{\:\:\:\:\mathrm{3}}&{−\mathrm{14}}&{−\mathrm{5}}\\{}&{}&{−\mathrm{2}}&{\:\:\:−\mathrm{1}}&{\:\:\mathrm{15}}\\{}&{\mathrm{2}}&{\:\:\:\:\mathrm{1}}&{−\mathrm{15}}&{\:\:\overset{{R}=} {\mathrm{10}}}\end{vmatrix} \\ $$$${q}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{15}\:,\:{R}=\mathrm{10} \\ $$$${q}\left({x}\right)\:{on}\:{dividing}\:{by}\:{x}+\mathrm{3}\:{gives} \\ $$$${remainder}\:\mathrm{0}\:{and}\:{quotient}\:{Px}+{Q} \\ $$$$\begin{vmatrix}{\left.−\mathrm{3}\right)}&{\mathrm{2}}&{\:\:\:\:\mathrm{1}}&{−\mathrm{15}}\\{}&{}&{−\mathrm{6}}&{+\mathrm{15}}\\{}&{\overset{{P}=} {\mathrm{2}}}&{\overset{{Q}=} {−\mathrm{5}}}&{\:\:\:\:\:\:\:\mathrm{0}}\end{vmatrix} \\ $$$${Px}+{Q}=\mathrm{2}{x}−\mathrm{5} \\ $$$${P}=\mathrm{2},\:{Q}=−\mathrm{5} \\ $$

Commented by Rasheed.Sindhi last updated on 20/Aug/20

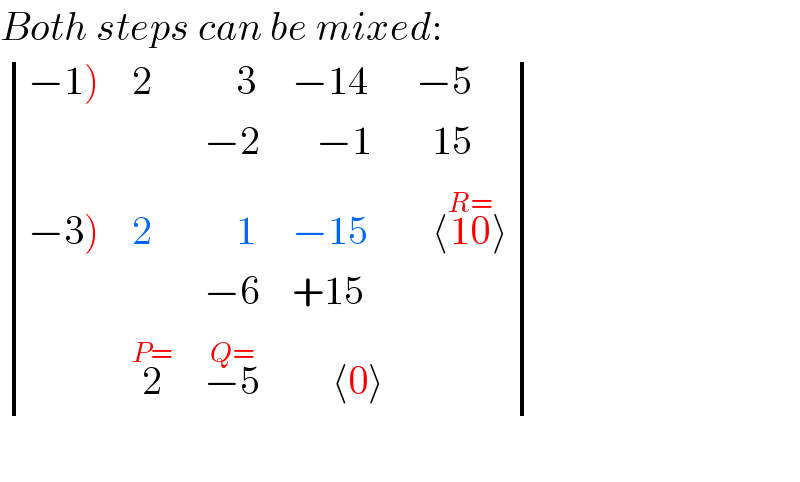
Both steps can be mixed: determinant (((−1)),2,( 3),(−14),(−5)),(,,(−2),( −1),( 15)),((−3)),2,( 1),(−15),( ⟨10^(R=) ⟩)),(,,(−6),(+15),),(,2^(P=) ,(−5^(Q=) ),( ⟨0⟩),))

$${Both}\:{steps}\:{can}\:{be}\:{mixed}: \\ $$$$\begin{vmatrix}{\left.−\mathrm{1}\right)}&{\mathrm{2}}&{\:\:\:\:\mathrm{3}}&{−\mathrm{14}}&{−\mathrm{5}}\\{}&{}&{−\mathrm{2}}&{\:\:\:−\mathrm{1}}&{\:\:\mathrm{15}}\\{\left.−\mathrm{3}\right)}&{\mathrm{2}}&{\:\:\:\:\mathrm{1}}&{−\mathrm{15}}&{\:\:\langle\overset{{R}=} {\mathrm{10}}\rangle}\\{}&{}&{−\mathrm{6}}&{+\mathrm{15}}&{}\\{}&{\overset{{P}=} {\mathrm{2}}}&{\overset{{Q}=} {−\mathrm{5}}}&{\:\:\:\:\:\langle\mathrm{0}\rangle}&{}\end{vmatrix} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com