Question Number 108961 by ZiYangLee last updated on 20/Aug/20
$$\mathrm{Solve}\:\frac{\mid{x}−\mathrm{2}\mid+\mathrm{1}}{\mid{x}−\mathrm{2}\mid−\mathrm{1}}<\mathrm{3} \\ $$
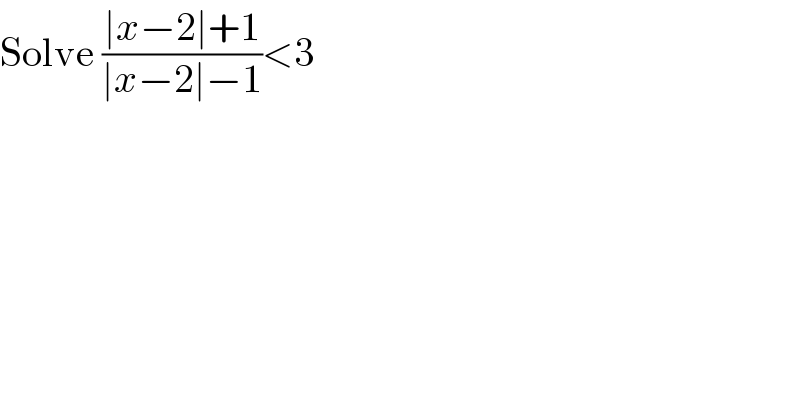
Commented byRasheed.Sindhi last updated on 20/Aug/20
$$\:\frac{\mid{x}−\mathrm{2}\mid+\mathrm{1}}{\mid{x}−\mathrm{2}\mid−\mathrm{1}}<\mathrm{3} \\ $$ $$\:\frac{\mid{x}−\mathrm{2}\mid+\mathrm{1}}{\mid{x}−\mathrm{2}\mid−\mathrm{1}}<\frac{\mathrm{2}+\mathrm{1}}{\mathrm{2}−\mathrm{1}} \\ $$ $$\:\frac{\mid{x}−\mathrm{2}\mid}{\mid{x}−\mathrm{2}\mid}<\frac{\mathrm{2}}{\mathrm{2}} \\ $$ $$\:\frac{\mid{x}−\mathrm{2}\mid}{\mid{x}−\mathrm{2}\mid}<\mathrm{1} \\ $$ $$?¿?¿?\:{Is}\:{this}\:{correct}\:?¿?¿? \\ $$
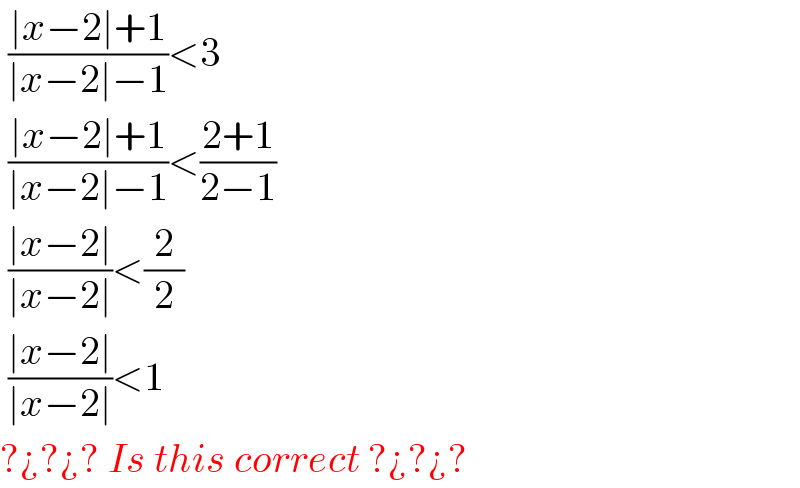
Commented bybemath last updated on 20/Aug/20
$${haha}..{not}\:{correct}\:\:\:{or}\:{false} \\ $$
Answered by 1549442205PVT last updated on 20/Aug/20
![Solve ((∣x−2∣+1)/(∣x−2∣−1))<3(1) Set x−2=y(y≥0)we have (1)⇔((y+1)/(y−1))<3⇔((y+1)/(y−1))−3<0 ⇔((−2y+4)/(y−1))<0⇔((−y+2)/(y−1))<0 ⇔y∈(−∞;1)∪(2;+∞) combining to the condition y≥0 we get y∈[0;1)∪(2;+∞) i)y∈[0;1) ⇔ ∣x−2∣<1 ⇔−1<x−2<1⇔1<x<3 ii)y∈(2;+∞)⇔∣x−2∣>2⇔ [((x−2>2⇔x>4)),((x−2<−2⇔x<0)) ] Combining (i)and (ii)we get x∈(1;3)∪(−∞;0)∪(4;+∞)](Q109073.png)
$$\mathrm{Solve}\:\frac{\mid{x}−\mathrm{2}\mid+\mathrm{1}}{\mid{x}−\mathrm{2}\mid−\mathrm{1}}<\mathrm{3}\left(\mathrm{1}\right) \\ $$ $$\mathrm{Set}\:\mathrm{x}−\mathrm{2}=\mathrm{y}\left(\mathrm{y}\geqslant\mathrm{0}\right)\mathrm{we}\:\mathrm{have} \\ $$ $$\left(\mathrm{1}\right)\Leftrightarrow\frac{\mathrm{y}+\mathrm{1}}{\mathrm{y}−\mathrm{1}}<\mathrm{3}\Leftrightarrow\frac{\mathrm{y}+\mathrm{1}}{\mathrm{y}−\mathrm{1}}−\mathrm{3}<\mathrm{0} \\ $$ $$\Leftrightarrow\frac{−\mathrm{2y}+\mathrm{4}}{\mathrm{y}−\mathrm{1}}<\mathrm{0}\Leftrightarrow\frac{−\mathrm{y}+\mathrm{2}}{\mathrm{y}−\mathrm{1}}<\mathrm{0} \\ $$ $$\Leftrightarrow\mathrm{y}\in\left(−\infty;\mathrm{1}\right)\cup\left(\mathrm{2};+\infty\right) \\ $$ $$\mathrm{combining}\:\mathrm{to}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{y}\geqslant\mathrm{0}\:\mathrm{we} \\ $$ $$\mathrm{get}\:\mathrm{y}\in\left[\mathrm{0};\mathrm{1}\right)\cup\left(\mathrm{2};+\infty\right) \\ $$ $$\left.\mathrm{i}\right)\mathrm{y}\in\left[\mathrm{0};\mathrm{1}\right)\:\Leftrightarrow\:\mid\mathrm{x}−\mathrm{2}\mid<\mathrm{1} \\ $$ $$\Leftrightarrow−\mathrm{1}<\mathrm{x}−\mathrm{2}<\mathrm{1}\Leftrightarrow\mathrm{1}<\mathrm{x}<\mathrm{3} \\ $$ $$\left.\mathrm{ii}\right)\mathrm{y}\in\left(\mathrm{2};+\infty\right)\Leftrightarrow\mid\mathrm{x}−\mathrm{2}\mid>\mathrm{2}\Leftrightarrow\begin{bmatrix}{\mathrm{x}−\mathrm{2}>\mathrm{2}\Leftrightarrow\mathrm{x}>\mathrm{4}}\\{\mathrm{x}−\mathrm{2}<−\mathrm{2}\Leftrightarrow\mathrm{x}<\mathrm{0}}\end{bmatrix} \\ $$ $$\mathrm{Combining}\:\left(\mathrm{i}\right)\mathrm{and}\:\left(\mathrm{ii}\right)\mathrm{we}\:\mathrm{get} \\ $$ $$\boldsymbol{\mathrm{x}}\in\left(\mathrm{1};\mathrm{3}\right)\cup\left(−\infty;\mathrm{0}\right)\cup\left(\mathrm{4};+\infty\right) \\ $$
Answered by john santu last updated on 20/Aug/20
$$\_\_\underset{\multimap} {{J}}\underset{\multimap} {{S}\_\_} \\ $$ $$\left(\mathrm{1}\right)\:\mid{x}−\mathrm{2}\mid\:\neq\:\mathrm{1}\:\rightarrow\begin{cases}{{x}\:\neq\:\mathrm{3}\:}\\{{x}\:\neq\:\mathrm{1}}\end{cases} \\ $$ $$\left(\mathrm{2}\right)\:{let}\:\mid{x}−\mathrm{2}\mid\:=\:{z}\:\rightarrow\frac{{z}+\mathrm{1}}{{z}−\mathrm{1}}\:<\:\mathrm{3} \\ $$ $$\frac{{z}−\mathrm{1}+\mathrm{2}}{{z}−\mathrm{1}}\:<\:\mathrm{3}\:\Rightarrow\:\mathrm{1}+\frac{\mathrm{2}}{{z}−\mathrm{1}}\:<\:\mathrm{3}\: \\ $$ $$\frac{\mathrm{2}}{{z}−\mathrm{1}}\:<\:\mathrm{2}\:\Rightarrow\:\frac{\mathrm{1}}{{z}−\mathrm{1}}\:<\:\frac{{z}−\mathrm{1}}{{z}−\mathrm{1}} \\ $$ $$\frac{\mathrm{2}−{z}}{{z}−\mathrm{1}}\:<\:\mathrm{0}\:\Rightarrow\:\frac{{z}−\mathrm{2}}{{z}−\mathrm{1}}\:>\:\mathrm{0} \\ $$ $${we}\:{got}\:{z}\:<\:\mathrm{1}\:{or}\:{z}\:>\:\mathrm{2}\: \\ $$ $${now}\:\mid{x}−\mathrm{2}\mid\:<\:\mathrm{1}\:{or}\:\mid{x}−\mathrm{2}\mid\:>\:\mathrm{2} \\ $$ $$\Rightarrow−\mathrm{1}<\:{x}−\mathrm{2}<\:\mathrm{1}\:{or}\:\left\{\:{x}\:>\:\mathrm{4}\:\cup\:{x}\:<\:\mathrm{0}\:\right\} \\ $$ $$\Rightarrow\mathrm{1}\:<\:{x}\:<\:\mathrm{3}\:{or}\:\left\{\:{x}\:<\:\mathrm{0}\:\cup\:{x}\:>\:\mathrm{4}\:\right\} \\ $$ $${the}\:{solution}\:{set}\:{is}\: \\ $$ $${x}\:\in\:\left(−\infty,\mathrm{0}\right)\:\cup\left(\mathrm{1},\mathrm{3}\right)\:\cup\:\left(\mathrm{4},\infty\right)\: \\ $$
Commented bybemath last updated on 20/Aug/20
$${waw}...{creative}\:{answer} \\ $$
Answered by Rasheed.Sindhi last updated on 21/Aug/20
$$\:\frac{\mid{x}−\mathrm{2}\mid+\mathrm{1}}{\mid{x}−\mathrm{2}\mid−\mathrm{1}}−\mathrm{1}<\mathrm{3}−\mathrm{1} \\ $$ $$\frac{\mathrm{2}}{\mid{x}−\mathrm{2}\mid}<\mathrm{2} \\ $$ $$\frac{\mathrm{1}}{\mid{x}−\mathrm{2}\mid}<\mathrm{1} \\ $$ $$\mid{x}−\mathrm{2}\mid>\mathrm{1\begin{cases}{{x}−\mathrm{2}>\mathrm{1}\Rightarrow{x}>\mathrm{3}}\\{−{x}+\mathrm{2}>\mathrm{1}\Rightarrow{x}<\mathrm{1}}\end{cases}} \\ $$ $$ \\ $$