Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 108967 by bobhans last updated on 20/Aug/20

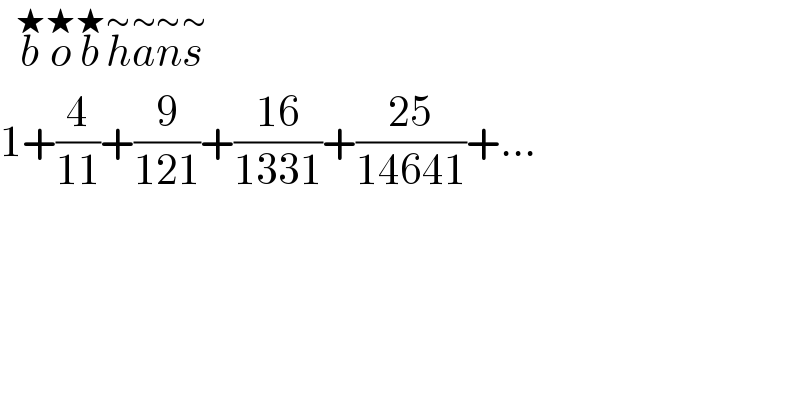
b^★ o^★ b^★ h^∼ a^∼ n^∼ s^∼ 1+(4/(11))+(9/(121))+((16)/(1331))+((25)/(14641))+...

$$\:\:\overset{\bigstar} {{b}}\overset{\bigstar} {{o}}\overset{\bigstar} {{b}}\overset{\sim} {{h}}\overset{\sim} {{a}}\overset{\sim} {{n}}\overset{\sim} {{s}} \\ $$$$\mathrm{1}+\frac{\mathrm{4}}{\mathrm{11}}+\frac{\mathrm{9}}{\mathrm{121}}+\frac{\mathrm{16}}{\mathrm{1331}}+\frac{\mathrm{25}}{\mathrm{14641}}+... \\ $$

Answered by john santu last updated on 20/Aug/20

⊸J_⊸ S_⊸ ⊸ consider gemetric series (1/(1−x)) = Σ_(n = 0) ^∞ x^n (d/dx)((1/(1−x))) = (d/dx)(Σ_(n = 0) ^∞ x^n ) (1/((1−x)^2 )) = Σ_(n = 0) ^∞ nx^(n−1) (x/((1−x)^2 )) = Σ_(n = 0) ^∞ nx^n diffrentiating both side ((1+x)/((1−x)^3 )) = Σ_(n = 0) ^∞ n^2 x^(n−1) letting x = (1/(11)) yields the desired result Σ_(n = 0) ^∞ (n^2 /(11^(n−1) )) = ((363)/(250))

$$\:\:\:\:\multimap\underset{\multimap} {{J}}\underset{\multimap} {{S}}\multimap \\ $$$${consider}\:{gemetric}\:{series}\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \\ $$$$\frac{{d}}{{dx}}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)\:=\:\frac{{d}}{{dx}}\left(\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \right) \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\:\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}{nx}^{{n}−\mathrm{1}} \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:=\:\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}{nx}^{{n}} \\ $$$${diffrentiating}\:{both}\:{side}\: \\ $$$$\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:=\:\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} \\ $$$${letting}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{11}}\:{yields}\:{the}\:{desired}\:{result} \\ $$$$\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{n}^{\mathrm{2}} }{\mathrm{11}^{{n}−\mathrm{1}} }\:=\:\frac{\mathrm{363}}{\mathrm{250}} \\ $$

Commented by bobhans last updated on 20/Aug/20

thank you all master

$${thank}\:{you}\:{all}\:{master} \\ $$

Answered by Dwaipayan Shikari last updated on 20/Aug/20

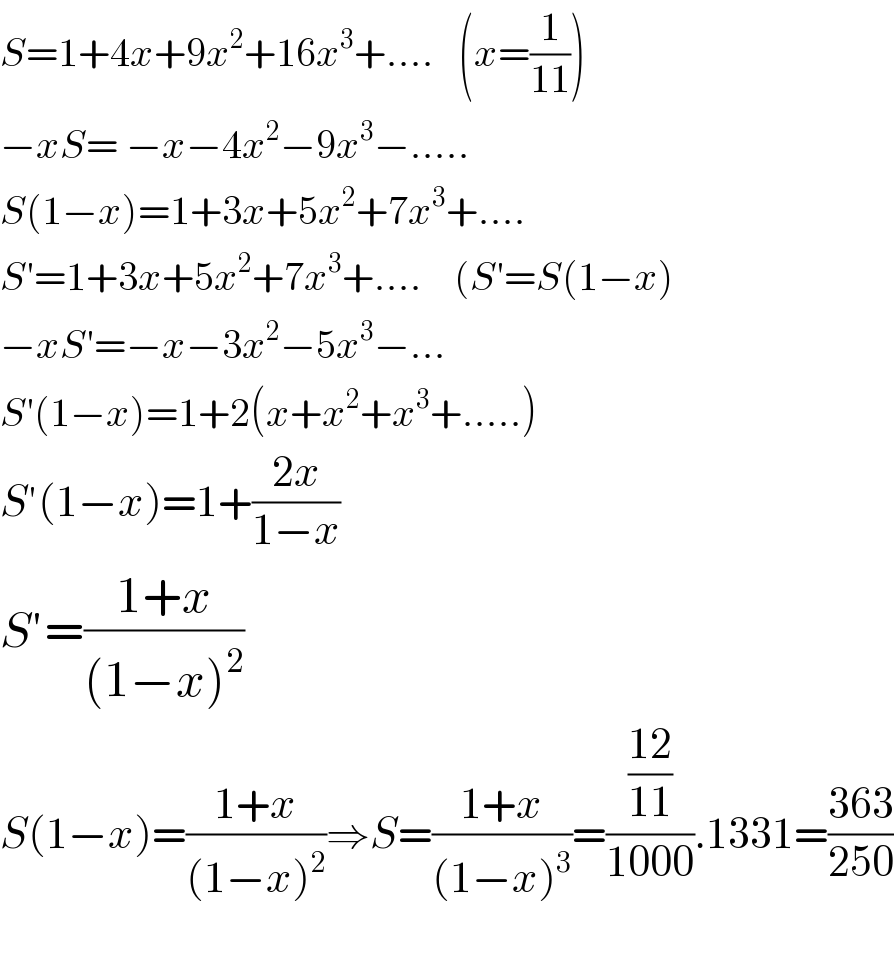
S=1+4x+9x^2 +16x^3 +.... (x=(1/(11))) −xS= −x−4x^2 −9x^3 −..... S(1−x)=1+3x+5x^2 +7x^3 +.... S′=1+3x+5x^2 +7x^3 +.... (S′=S(1−x) −xS′=−x−3x^2 −5x^3 −... S′(1−x)=1+2(x+x^2 +x^3 +.....) S′(1−x)=1+((2x)/(1−x)) S′=((1+x)/((1−x)^2 )) S(1−x)=((1+x)/((1−x)^2 ))⇒S=((1+x)/((1−x)^3 ))=(((12)/(11))/(1000)).1331=((363)/(250))

$${S}=\mathrm{1}+\mathrm{4}{x}+\mathrm{9}{x}^{\mathrm{2}} +\mathrm{16}{x}^{\mathrm{3}} +....\:\:\:\left({x}=\frac{\mathrm{1}}{\mathrm{11}}\right) \\ $$$$−{xS}=\:−{x}−\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}{x}^{\mathrm{3}} −..... \\ $$$${S}\left(\mathrm{1}−{x}\right)=\mathrm{1}+\mathrm{3}{x}+\mathrm{5}{x}^{\mathrm{2}} +\mathrm{7}{x}^{\mathrm{3}} +.... \\ $$$${S}'=\mathrm{1}+\mathrm{3}{x}+\mathrm{5}{x}^{\mathrm{2}} +\mathrm{7}{x}^{\mathrm{3}} +....\:\:\:\:\left({S}'={S}\left(\mathrm{1}−{x}\right)\right. \\ $$$$−{xS}'=−{x}−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{5}{x}^{\mathrm{3}} −... \\ $$$${S}'\left(\mathrm{1}−{x}\right)=\mathrm{1}+\mathrm{2}\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +.....\right) \\ $$$${S}'\left(\mathrm{1}−{x}\right)=\mathrm{1}+\frac{\mathrm{2}{x}}{\mathrm{1}−{x}} \\ $$$${S}'=\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${S}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\Rightarrow{S}=\frac{\mathrm{1}+{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\frac{\frac{\mathrm{12}}{\mathrm{11}}}{\mathrm{1000}}.\mathrm{1331}=\frac{\mathrm{363}}{\mathrm{250}} \\ $$$$ \\ $$

Answered by nimnim last updated on 20/Aug/20

Let S=1+(4/(11))+(9/(11^2 ))+((16)/(11^3 ))+((25)/(11^4 ))+........(1) 11S=11+4+(9/(11))+((16)/(11^2 ))+((25)/(11^3 ))+((36)/(11^4 ))+.....(2) {(1)×11} ∴ 10S=14+(5/(11))+(7/(11^2 ))+(9/(11^3 ))+((11)/(11^4 ))+.......(3) {(2)−(1)} also, (S/(11))=(1/(11))+(4/(11^2 ))+(9/(11^3 ))+((16)/(11^4 ))+((25)/(11^5 ))+....(4) {(1)÷11} ∴ ((10)/(11))S=1+(3/(11))+(5/(11^2 ))+(7/(11^3 ))+(9/(11^4 ))+......(5) {(1)−(4)} ((100)/(11))S=13+(2/(11))+(2/(11^2 ))+(2/(11^3 ))+......... {(3)−(5)} =13+2[((1/(11))/(1−(1/(11))))]=13+(1/5)=((66)/5) ∴ S=((66)/5)×((11)/(100))=((363)/(250))★

$${Let}\:\:\:{S}=\mathrm{1}+\frac{\mathrm{4}}{\mathrm{11}}+\frac{\mathrm{9}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{16}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{25}}{\mathrm{11}^{\mathrm{4}} }+........\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\mathrm{11}{S}=\mathrm{11}+\mathrm{4}+\frac{\mathrm{9}}{\mathrm{11}}+\frac{\mathrm{16}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{25}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{36}}{\mathrm{11}^{\mathrm{4}} }+.....\left(\mathrm{2}\right)\:\:\:\:\:\:\left\{\left(\mathrm{1}\right)×\mathrm{11}\right\} \\ $$$$\therefore\:\mathrm{10}{S}=\mathrm{14}+\frac{\mathrm{5}}{\mathrm{11}}+\frac{\mathrm{7}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{11}}{\mathrm{11}^{\mathrm{4}} }+.......\left(\mathrm{3}\right)\:\:\:\:\:\:\left\{\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\right\} \\ $$$$\:{also},\:\frac{{S}}{\mathrm{11}}=\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{4}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{9}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{16}}{\mathrm{11}^{\mathrm{4}} }+\frac{\mathrm{25}}{\mathrm{11}^{\mathrm{5}} }+....\left(\mathrm{4}\right)\:\:\:\:\:\left\{\left(\mathrm{1}\right)\boldsymbol{\div}\mathrm{11}\right\} \\ $$$$\therefore\:\frac{\mathrm{10}}{\mathrm{11}}{S}=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{11}}+\frac{\mathrm{5}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{11}^{\mathrm{3}} }+\frac{\mathrm{9}}{\mathrm{11}^{\mathrm{4}} }+......\left(\mathrm{5}\right)\:\:\:\:\:\left\{\left(\mathrm{1}\right)−\left(\mathrm{4}\right)\right\} \\ $$$$\frac{\mathrm{100}}{\mathrm{11}}{S}=\mathrm{13}+\frac{\mathrm{2}}{\mathrm{11}}+\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{11}^{\mathrm{3}} }+.........\:\:\left\{\left(\mathrm{3}\right)−\left(\mathrm{5}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{13}+\mathrm{2}\left[\frac{\frac{\mathrm{1}}{\mathrm{11}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{11}}}\right]=\mathrm{13}+\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{66}}{\mathrm{5}} \\ $$$$\therefore\:{S}=\frac{\mathrm{66}}{\mathrm{5}}×\frac{\mathrm{11}}{\mathrm{100}}=\frac{\mathrm{363}}{\mathrm{250}}\bigstar \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com