
Question and Answers Forum
Question Number 109178 by Algoritm last updated on 21/Aug/20

Commented by Algoritm last updated on 21/Aug/20

Answered by Dwaipayan Shikari last updated on 21/Aug/20
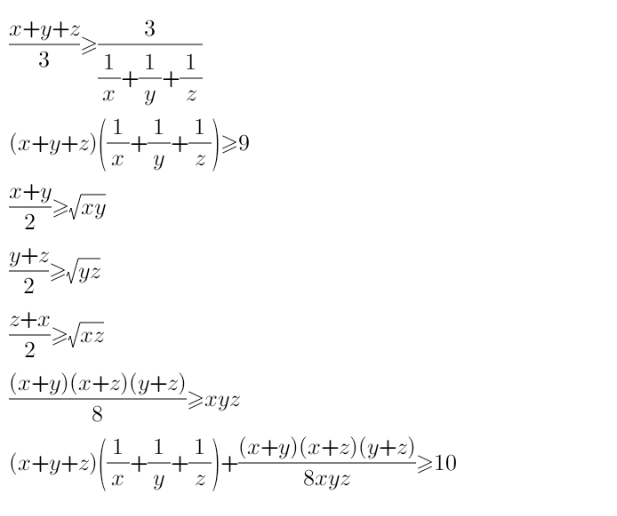
Commented by Algoritm last updated on 21/Aug/20

Commented by aurpeyz last updated on 21/Aug/20
Commented by floor(10²Eta[1]) last updated on 22/Aug/20

Answered by 1549442205PVT last updated on 22/Aug/20
![We have: (x+y+z)((1/x)+(1/y)+(1/z))+((8xyz)/((x+y)(y+z)(z+x)))≥10 ⇔(((x+y+z)(xy+yz+zx))/(xyz))+((8xyz)/((x+y)(y+z)(z+x)))≥10(1) First,we note some following identities: (x+y)(y+z)(z+x)=(x+y+z)(xy+yz+zx)−xyz Hence,The inequality (1) is equivalent to (((x+y+z)(xy+yz+zx))/(xyz))+((8xyz)/((x+y+z)(xy+yz+zx)−xyz))≥10(2) Since the nominator and denomirator of each the fraction in the LHS are in same degree (degree 3),WLOG we can suppose that x+y+z=3(because if x+y+z=m then put x=((am)/3),y=((bm)/3), z=((cm)/3)⇒((am)/3)+((bm)/3)+((cm)/3)=m⇒a+b+c=3 and the inequality (2) becomes (((m/3)^3 (a+b+c)(ab+bc+ca))/((m/3)^3 abc))+((8(m/3)^3 abc)/((m/3)^3 [(a+b+c)(ab+bc+ca)−abc]))≥10 ⇔(( (a+b+c)(ab+bc+ca))/(abc))+((8abc)/((a+b+c)(ab+bc+ca)−abc))≥10 which is also the inequality (2) but under the condition a+b+c=3) By that reason we have (2)⇔((3(xy+yz+zx))/(xyz))+((8xyz)/(3(xy+yz+zx)−xyz))≥10 ⇔9(xy+yz+zx)^2 −3xyz(xy+yz+zx) +18(xyz)^2 ≥10xyz[3(xy+yz+zx)−xyz] ⇔9(xy+yz+zx)^2 +18(xyz)^2 ≥ 33xyz(xy+yz+zx)(3) Now we put xy=m,xz=n,yz=p.Then 3^2 =(x+y+z)^2 ≥3(xy+yz+zx) ⇒m+n+p=xy+yz+zx≤3 3≥xy+yz+zx≥3^3 (√(xy.yz.zx))=3^3 (√((xyz)^2 )) ⇒^3 (√(xyz)) ≤1,mnp≤(((m+m+p)/3))^3 ≤1(∗) We have also (xyz)^2 =mnp.Therefore, (3)⇔9(m+n+p)^2 +18mnp≥33(m+n+p)(√(mnp)) (3′) Apply Cauchy′s inequality for two positive numbers we have 2(m+n+p)^2 +18mnp≥(√(2(m+n+p)^2 .8mnp)) =8(m+n+p)(√(mnp)) (i).On the other hands, Since mnp≤1⇒(√(mnp)) ≤1(due to (∗)) ⇒mnp(√(mnp))=(√((mnp)^3 ))≤mnp ⇒(√(mnp))≤^3 (√(mnp)) (∗∗).Now apply Cauchy′s inequality for three positive numbers we get: m^2 +mn+mp≥3^3 (√(m^2 .mn.mp)) =3m^3 (√(mnp)) ≥3(√(mnp)) (due to (∗∗)).Similarly, n^2 +nm+np≥3n(√(mnp)) p^2 +pn+pm≥3p(√(mnp)) Adding up three above inequalities we get m^2 +n^2 +p^2 +2(mn+mp+np) =(m+n+p)^2 ≥3(m+n+p)(√(mnp)) ⇒7(m+n+p)^3 ≥21(m+n+p)(√(mnp))(ii) Adding up two inequalities (i)and(ii) we get: 9(m+n+p)^2 +18mnp≥33(m+n+p)(√(mnp)) ,so the inequality (3′)is true which implies that (2) is true .Consequently, the inequality (1)is proved.Thus,we proved the inequality: (x+y+z)((1/x)+(1/y)+(1/z))+((8xyz)/((x+y)(y+z)(z+x)))≥10 The equality ocurrs if and only if x=y=z (Q.E.D)](Q109252.png)
