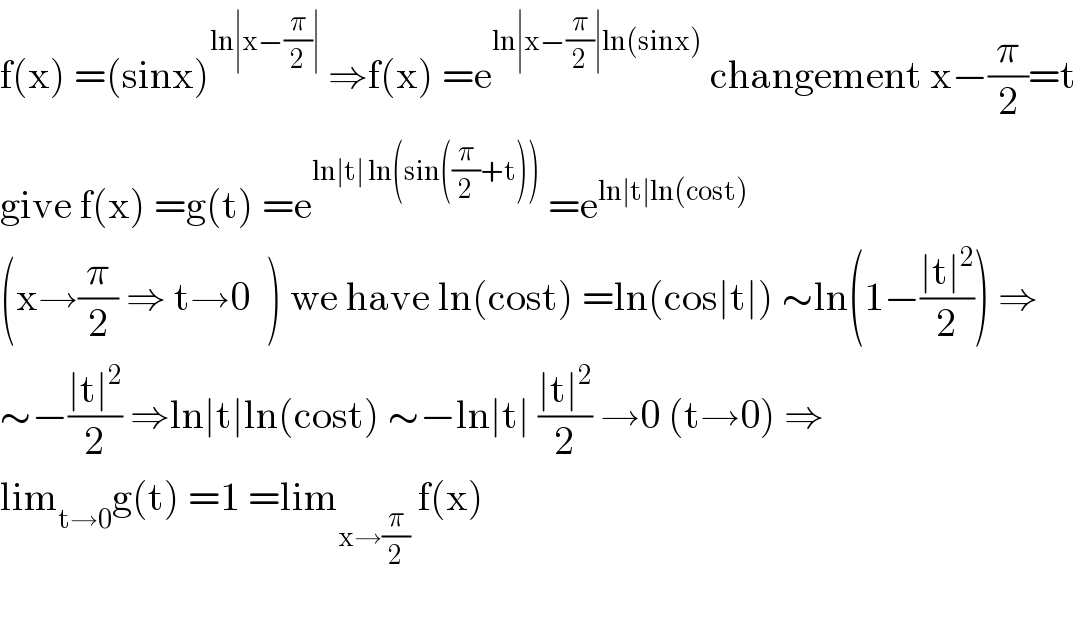Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 109191 by abdomsup last updated on 21/Aug/20

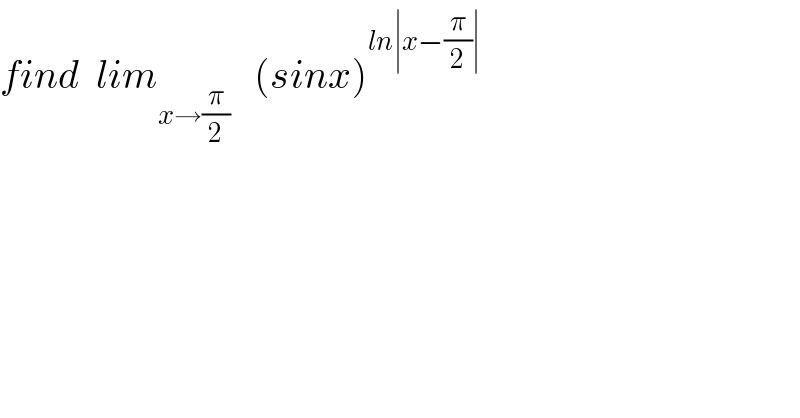
find lim_(x→(π/2)) (sinx)^(ln∣x−(π/2)∣)

$${find}\:\:{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:\:\left({sinx}\right)^{{ln}\mid{x}−\frac{\pi}{\mathrm{2}}\mid} \\ $$

Commented by bemath last updated on 22/Aug/20

set x = (π/2)+ z L= lim_(z→0) (sin ((π/2)+z))^(ln ∣z∣) =lim_(z→0) (cos z)^(ln ∣z∣) ln L = lim_(z→0) ln ∣z∣ (cos z) ln L = lim_(z→0) ((cos z)/(1/(ln z))) = lim_(z→0) ((−sin z)/([((−(1/z))/(ln^2 (z)))])) ln L=lim_(z→0) sin z .((ln^2 z)/(1/z))=lim_(z→0) z.sin z.ln^2 z ln L = 0 ⇒ L = e^0 = 1

$${set}\:{x}\:=\:\frac{\pi}{\mathrm{2}}+\:{z} \\ $$$${L}=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+{z}\right)\right)^{\mathrm{ln}\:\mid{z}\mid} =\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}\:{z}\right)^{\mathrm{ln}\:\mid{z}\mid} \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\:\mid{z}\mid\:\left(\mathrm{cos}\:{z}\right) \\ $$$$\mathrm{ln}\:{L}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:{z}}{\frac{\mathrm{1}}{\mathrm{ln}\:{z}}}\:=\:\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:{z}}{\left[\frac{−\frac{\mathrm{1}}{{z}}}{\mathrm{ln}\:^{\mathrm{2}} \left({z}\right)}\right]} \\ $$$$\mathrm{ln}\:{L}=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{sin}\:{z}\:.\frac{\mathrm{ln}\:^{\mathrm{2}} {z}}{\frac{\mathrm{1}}{{z}}}=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{z}.\mathrm{sin}\:{z}.\mathrm{ln}\:^{\mathrm{2}} \:{z} \\ $$$$\mathrm{ln}\:{L}\:=\:\mathrm{0}\:\Rightarrow\:{L}\:=\:{e}^{\mathrm{0}} \:=\:\mathrm{1} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 23/Aug/20

f(x) =(sinx)^(ln∣x−(π/2)∣) ⇒f(x) =e^(ln∣x−(π/2)∣ln(sinx)) changement x−(π/2)=t give f(x) =g(t) =e^(ln∣t∣ ln(sin((π/2)+t))) =e^(ln∣t∣ln(cost)) (x→(π/2) ⇒ t→0 ) we have ln(cost) =ln(cos∣t∣) ∼ln(1−((∣t∣^2 )/2)) ⇒ ∼−((∣t∣^2 )/2) ⇒ln∣t∣ln(cost) ∼−ln∣t∣ ((∣t∣^2 )/2) →0 (t→0) ⇒ lim_(t→0) g(t) =1 =lim_(x→(π/2)) f(x)

$$\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{sinx}\right)^{\mathrm{ln}\mid\mathrm{x}−\frac{\pi}{\mathrm{2}}\mid} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{ln}\mid\mathrm{x}−\frac{\pi}{\mathrm{2}}\mid\mathrm{ln}\left(\mathrm{sinx}\right)} \:\mathrm{changement}\:\mathrm{x}−\frac{\pi}{\mathrm{2}}=\mathrm{t} \\ $$$$\mathrm{give}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{g}\left(\mathrm{t}\right)\:=\mathrm{e}^{\mathrm{ln}\mid\mathrm{t}\mid\:\mathrm{ln}\left(\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}+\mathrm{t}\right)\right)} \:=\mathrm{e}^{\mathrm{ln}\mid\mathrm{t}\mid\mathrm{ln}\left(\mathrm{cost}\right)} \\ $$$$\left(\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{t}\rightarrow\mathrm{0}\:\:\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\mathrm{cost}\right)\:=\mathrm{ln}\left(\mathrm{cos}\mid\mathrm{t}\mid\right)\:\sim\mathrm{ln}\left(\mathrm{1}−\frac{\mid\mathrm{t}\mid^{\mathrm{2}} }{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\sim−\frac{\mid\mathrm{t}\mid^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{ln}\mid\mathrm{t}\mid\mathrm{ln}\left(\mathrm{cost}\right)\:\sim−\mathrm{ln}\mid\mathrm{t}\mid\:\frac{\mid\mathrm{t}\mid^{\mathrm{2}} }{\mathrm{2}}\:\rightarrow\mathrm{0}\:\left(\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)\:=\mathrm{1}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} \:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com