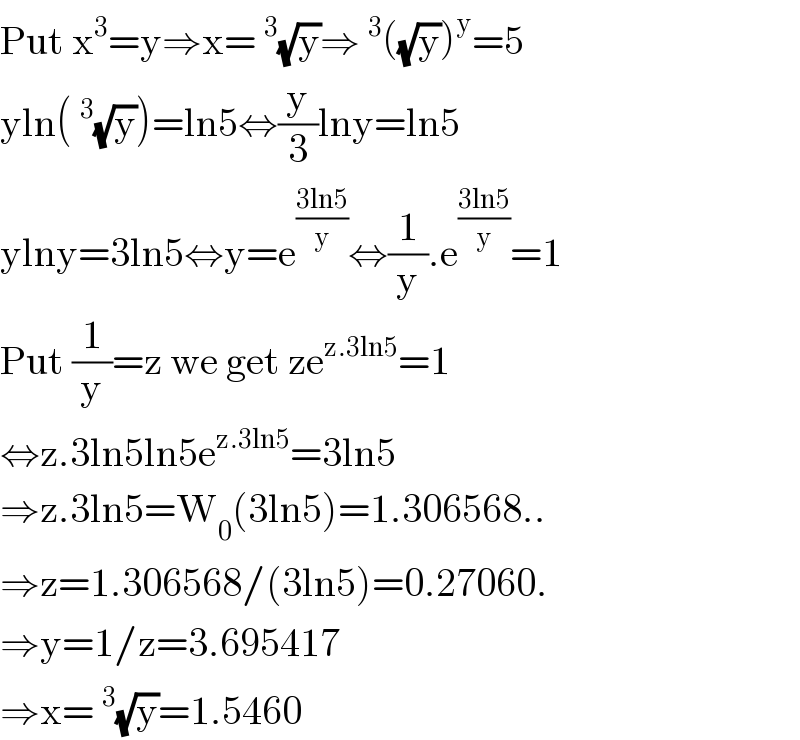Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 109193 by mr W last updated on 21/Aug/20

solve x^x^3 =5

$${solve}\: \\ $$$${x}^{{x}^{\mathrm{3}} } =\mathrm{5} \\ $$

Commented by aurpeyz last updated on 21/Aug/20

x^x^3 =2^2 x^3 =2 x=^3 _ (√2)

$$\:{x}^{{x}^{\mathrm{3}} } =\mathrm{2}^{\mathrm{2}} \\ $$$${x}^{\mathrm{3}} =\mathrm{2} \\ $$$${x}\underset{} {=}^{\mathrm{3}} \sqrt{\mathrm{2}} \\ $$

Commented by aurpeyz last updated on 21/Aug/20

i just tried. pls correct me

$${i}\:{just}\:{tried}.\:{pls}\:{correct}\:{me} \\ $$

Commented by mr W last updated on 21/Aug/20

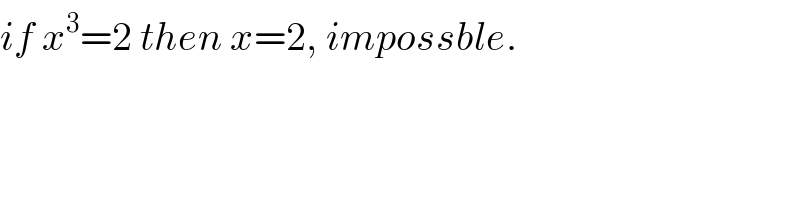
if x^3 =2 then x=2, impossble.

$${if}\:{x}^{\mathrm{3}} =\mathrm{2}\:{then}\:{x}=\mathrm{2},\:{impossble}. \\ $$

Commented by mr W last updated on 21/Aug/20

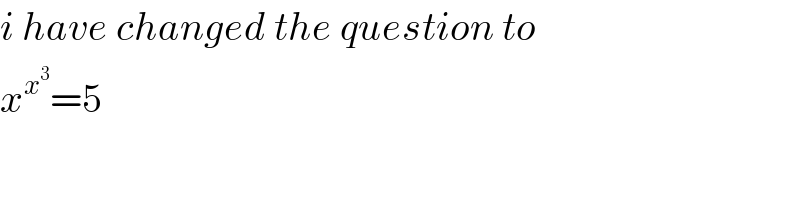
i have changed the question to x^x^3 =5

$${i}\:{have}\:{changed}\:{the}\:{question}\:{to} \\ $$$${x}^{{x}^{\mathrm{3}} } =\mathrm{5} \\ $$

Commented by aurpeyz last updated on 21/Aug/20

i wrote cube root of 2

$${i}\:{wrote}\:{cube}\:{root}\:{of}\:\mathrm{2} \\ $$

Commented by aurpeyz last updated on 21/Aug/20

okay sir. i will try

$${okay}\:{sir}.\:{i}\:{will}\:{try} \\ $$

Commented by mr W last updated on 21/Aug/20

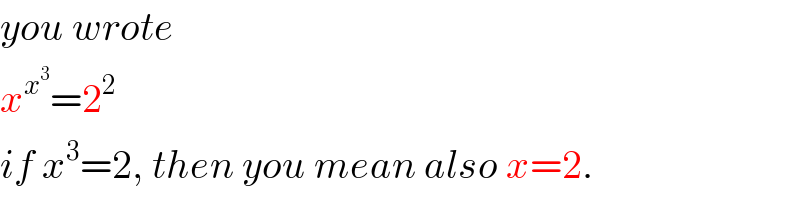
you wrote x^x^3 =2^2 if x^3 =2, then you mean also x=2.

$${you}\:{wrote} \\ $$$${x}^{{x}^{\mathrm{3}} } =\mathrm{2}^{\mathrm{2}} \\ $$$${if}\:{x}^{\mathrm{3}} =\mathrm{2},\:{then}\:{you}\:{mean}\:{also}\:{x}=\mathrm{2}. \\ $$

Commented by aurpeyz last updated on 21/Aug/20

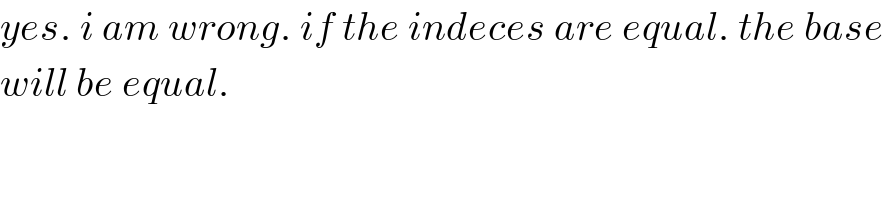
yes. i am wrong. if the indeces are equal. the base will be equal.

$${yes}.\:{i}\:{am}\:{wrong}.\:{if}\:{the}\:{indeces}\:{are}\:{equal}.\:{the}\:{base} \\ $$$${will}\:{be}\:{equal}. \\ $$

Answered by Dwaipayan Shikari last updated on 21/Aug/20

x^3 logx=log5 3logx e^(3logx) =3log5 3logx=W_0 (3log5) x=e^((W_0 (3log5))/3) =1.5459..

$${x}^{\mathrm{3}} {logx}={log}\mathrm{5} \\ $$$$\mathrm{3}{logx}\:{e}^{\mathrm{3}{logx}} =\mathrm{3}{log}\mathrm{5} \\ $$$$\mathrm{3}{logx}={W}_{\mathrm{0}} \left(\mathrm{3}{log}\mathrm{5}\right) \\ $$$${x}={e}^{\frac{{W}_{\mathrm{0}} \left(\mathrm{3}{log}\mathrm{5}\right)}{\mathrm{3}}} =\mathrm{1}.\mathrm{5459}.. \\ $$

Commented by mr W last updated on 21/Aug/20

good!

$${good}! \\ $$

Answered by Aziztisffola last updated on 21/Aug/20

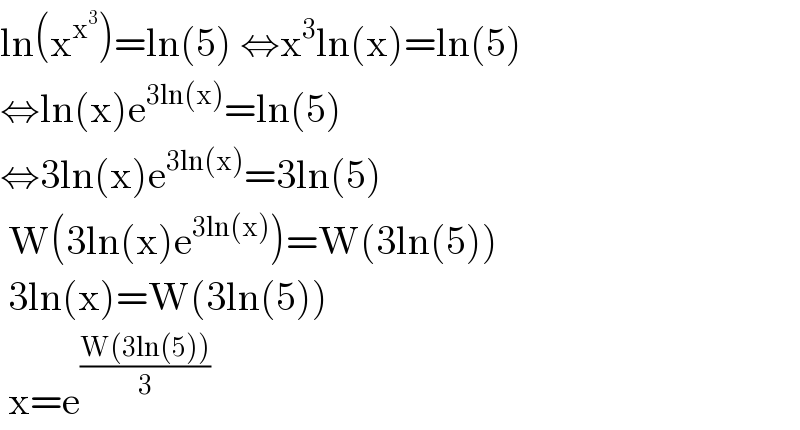
ln(x^x^3 )=ln(5) ⇔x^3 ln(x)=ln(5) ⇔ln(x)e^(3ln(x)) =ln(5) ⇔3ln(x)e^(3ln(x)) =3ln(5) W(3ln(x)e^(3ln(x)) )=W(3ln(5)) 3ln(x)=W(3ln(5)) x=e^((W(3ln(5)))/3)

$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{x}^{\mathrm{3}} } \right)=\mathrm{ln}\left(\mathrm{5}\right)\:\Leftrightarrow\mathrm{x}^{\mathrm{3}} \mathrm{ln}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{5}\right) \\ $$$$\Leftrightarrow\mathrm{ln}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{3ln}\left(\mathrm{x}\right)} =\mathrm{ln}\left(\mathrm{5}\right) \\ $$$$\Leftrightarrow\mathrm{3ln}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{3ln}\left(\mathrm{x}\right)} =\mathrm{3ln}\left(\mathrm{5}\right) \\ $$$$\:\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{x}\right)\mathrm{e}^{\mathrm{3ln}\left(\mathrm{x}\right)} \right)=\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{5}\right)\right) \\ $$$$\:\mathrm{3ln}\left(\mathrm{x}\right)=\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{5}\right)\right) \\ $$$$\:\mathrm{x}=\mathrm{e}^{\frac{\mathrm{W}\left(\mathrm{3ln}\left(\mathrm{5}\right)\right)}{\mathrm{3}}} \\ $$

Commented by aurpeyz last updated on 24/Aug/20

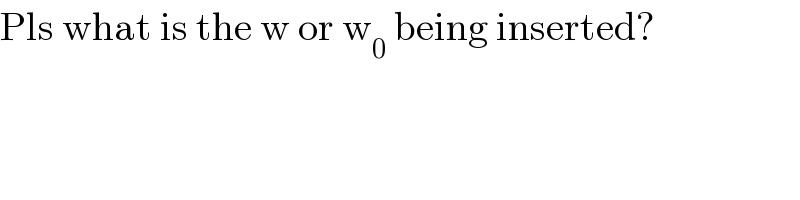
Pls what is the w or w_0 being inserted?

$$\mathrm{Pls}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{w}\:\mathrm{or}\:\mathrm{w}_{\mathrm{0}} \:\mathrm{being}\:\mathrm{inserted}? \\ $$

Commented by Aziztisffola last updated on 24/Aug/20

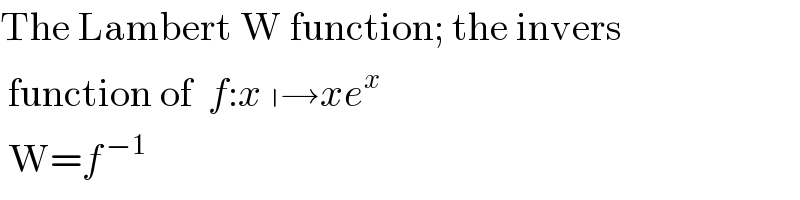
The Lambert W function; the invers function of f:x ∣→xe^x W=f^( −1 )

$$\mathrm{The}\:\mathrm{Lambert}\:\mathrm{W}\:\mathrm{function};\:\mathrm{the}\:\mathrm{invers}\: \\ $$$$\:\mathrm{function}\:\mathrm{of}\:\:{f}:{x}\:\shortmid\rightarrow{xe}^{{x}} \\ $$$$\:\mathrm{W}={f}^{\:−\mathrm{1}\:} \\ $$

Commented by aurpeyz last updated on 25/Aug/20

wow. that was why you multiplied through by 3?

$${wow}.\:{that}\:{was}\:{why}\:{you}\:{multiplied}\:{through} \\ $$$${by}\:\mathrm{3}? \\ $$

Answered by 1549442205PVT last updated on 22/Aug/20

Put x^3 =y⇒x=^3 (√y)⇒^3 ((√y))^y =5 yln(^3 (√y))=ln5⇔(y/3)lny=ln5 ylny=3ln5⇔y=e^((3ln5)/y) ⇔(1/y).e^((3ln5)/y) =1 Put (1/y)=z we get ze^(z.3ln5) =1 ⇔z.3ln5ln5e^(z.3ln5) =3ln5 ⇒z.3ln5=W_0 (3ln5)=1.306568.. ⇒z=1.306568/(3ln5)=0.27060. ⇒y=1/z=3.695417 ⇒x=^3 (√y)=1.5460

$$\mathrm{Put}\:\mathrm{x}^{\mathrm{3}} =\mathrm{y}\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\mathrm{y}}\Rightarrow\:^{\mathrm{3}} \left(\sqrt{\mathrm{y}}\right)^{\mathrm{y}} =\mathrm{5} \\ $$$$\mathrm{yln}\left(\:^{\mathrm{3}} \sqrt{\mathrm{y}}\right)=\mathrm{ln5}\Leftrightarrow\frac{\mathrm{y}}{\mathrm{3}}\mathrm{lny}=\mathrm{ln5} \\ $$$$\mathrm{ylny}=\mathrm{3ln5}\Leftrightarrow\mathrm{y}=\mathrm{e}^{\frac{\mathrm{3ln5}}{\mathrm{y}}} \Leftrightarrow\frac{\mathrm{1}}{\mathrm{y}}.\mathrm{e}^{\frac{\mathrm{3ln5}}{\mathrm{y}}} =\mathrm{1} \\ $$$$\mathrm{Put}\:\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{z}\:\mathrm{we}\:\mathrm{get}\:\mathrm{ze}^{\mathrm{z}.\mathrm{3ln5}} =\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{z}.\mathrm{3ln5ln5e}^{\mathrm{z}.\mathrm{3ln5}} =\mathrm{3ln5} \\ $$$$\Rightarrow\mathrm{z}.\mathrm{3ln5}=\mathrm{W}_{\mathrm{0}} \left(\mathrm{3ln5}\right)=\mathrm{1}.\mathrm{306568}.. \\ $$$$\Rightarrow\mathrm{z}=\mathrm{1}.\mathrm{306568}/\left(\mathrm{3ln5}\right)=\mathrm{0}.\mathrm{27060}. \\ $$$$\Rightarrow\mathrm{y}=\mathrm{1}/\mathrm{z}=\mathrm{3}.\mathrm{695417} \\ $$$$\Rightarrow\mathrm{x}=\:^{\mathrm{3}} \sqrt{\mathrm{y}}=\mathrm{1}.\mathrm{5460} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com