Question Number 109305 by peter frank last updated on 22/Aug/20
Answered by Aziztisffola last updated on 22/Aug/20
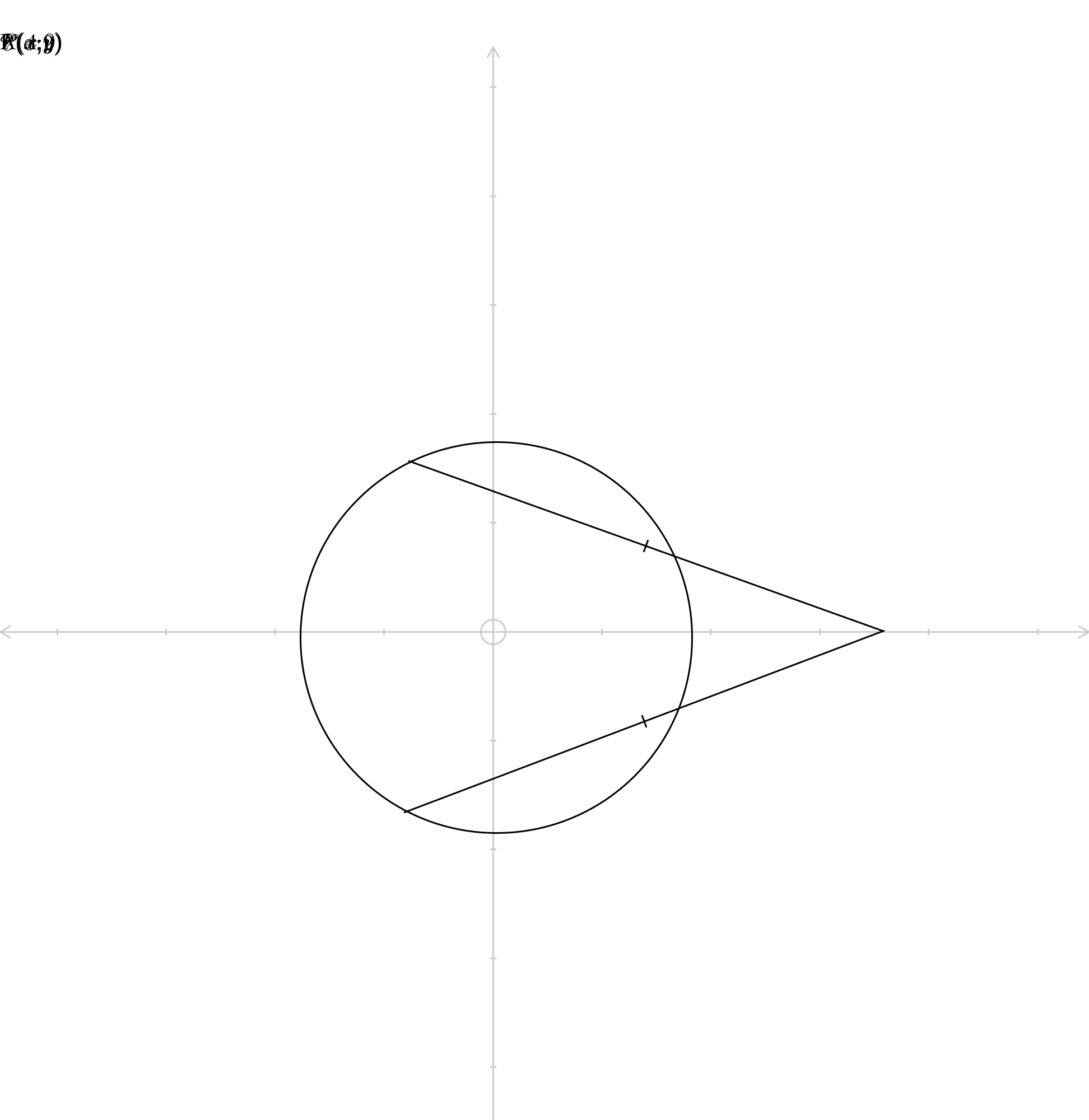
![let A(4;0) and P(x;y)∈C(o;2) ⇒x^2 +y^2 =4 ⇒ y=+_− (√(4−x^2 )) let I be center of [AP] I(((x+4)/2);((√(4−x^2 ))/2)) ∧ I(((x+4)/2);−((√(4−x^2 ))/2))](Q109323.png)
$$\:\mathrm{let}\:\mathrm{A}\left(\mathrm{4};\mathrm{0}\right)\:\mathrm{and}\:\mathrm{P}\left({x};{y}\right)\in\mathscr{C}\left(\mathrm{o};\mathrm{2}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\:{y}=\underset{−} {+}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{let}\:\mathrm{I}\:\mathrm{be}\:\mathrm{center}\:\mathrm{of}\:\left[\mathrm{AP}\right] \\ $$$$\:\mathrm{I}\left(\frac{{x}+\mathrm{4}}{\mathrm{2}};\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\mathrm{2}}\right)\:\:\wedge\:\mathrm{I}\left(\frac{{x}+\mathrm{4}}{\mathrm{2}};−\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\mathrm{2}}\right) \\ $$
Commented by Aziztisffola last updated on 22/Aug/20
$$ \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 22/Aug/20
![P(x_1 ,y_1 )∈(O,2)⇒x_1 ^2 +y_1 ^2 =4⇒y_1 =±(√(4−x^2 )) ⇒P(x_1 ,±(√(4−x_1 ^2 ))),I −midpoint of AP (since by the hypothesis AI:AP=1:2) since A(4,0),we have I(((x_1 +4)/2),((±(√(4−x_1 ^2 )))/2)) If denote by (x,y)−the coordinates of the point I then we have { ((x=((x_1 +4)/2) (1))),((y=((±(√(4−x_1 ^2 )))/2) (2))) :} From (2) we get (2y)^2 =4−x_1 ^2 ⇒4−x_1 ^2 =4y^2 ⇒x_1 ^2 =4(1−y^2 )(3) From (1) we get x_1 ^2 =(2x−4)^2 =[2(x−2)]^2 =4(x−2)^2 (4) From (3)and (4)we get 1−y^2 =(x−2)^2 ⇔(x−2)^2 +y^2 =1 This shows that the point I runs on the circle with the centre having the cordinates be (2,0) and the radius equal to 1 when P remove on (O,2)](Q109331.png)
$$\mathrm{P}\left(\mathrm{x}_{\mathrm{1}} ,\mathrm{y}_{\mathrm{1}} \right)\in\left(\mathrm{O},\mathrm{2}\right)\Rightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4}\Rightarrow\mathrm{y}_{\mathrm{1}} =\pm\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x}_{\mathrm{1}} ,\pm\sqrt{\mathrm{4}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} }\right),\mathrm{I}\:−\mathrm{midpoint}\:\mathrm{of}\:\mathrm{AP} \\ $$$$\left(\mathrm{since}\:\mathrm{by}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{AI}:\mathrm{AP}=\mathrm{1}:\mathrm{2}\right) \\ $$$$\mathrm{since}\:\mathrm{A}\left(\mathrm{4},\mathrm{0}\right),\mathrm{we}\:\mathrm{have}\:\mathrm{I}\left(\frac{\mathrm{x}_{\mathrm{1}} +\mathrm{4}}{\mathrm{2}},\frac{\pm\sqrt{\mathrm{4}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} }}{\mathrm{2}}\right) \\ $$$$\mathrm{If}\:\mathrm{denote}\:\mathrm{by}\:\left(\mathrm{x},\mathrm{y}\right)−\mathrm{the}\:\mathrm{coordinates}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{point}\:\mathrm{I}\:\mathrm{then}\:\mathrm{we}\:\mathrm{have} \\ $$$$\begin{cases}{\mathrm{x}=\frac{\mathrm{x}_{\mathrm{1}} +\mathrm{4}}{\mathrm{2}}\:\left(\mathrm{1}\right)}\\{\mathrm{y}=\frac{\pm\sqrt{\mathrm{4}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} }}{\mathrm{2}}\:\:\left(\mathrm{2}\right)}\end{cases}\: \\ $$$$\mathrm{From}\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\left(\mathrm{2y}\right)^{\mathrm{2}} =\mathrm{4}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} \:\: \\ $$$$\Rightarrow\mathrm{4}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4y}^{\mathrm{2}} \Rightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} =\left(\mathrm{2x}−\mathrm{4}\right)^{\mathrm{2}} \\ $$$$=\left[\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)\right]^{\mathrm{2}} =\mathrm{4}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{4}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{3}\right)\mathrm{and}\:\left(\mathrm{4}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{1}−\mathrm{y}^{\mathrm{2}} =\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \Leftrightarrow\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{This}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{the}\:\mathrm{point}\:\mathrm{I}\:\mathrm{runs}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{having} \\ $$$$\mathrm{the}\:\mathrm{cordinates}\:\mathrm{be}\:\left(\mathrm{2},\mathrm{0}\right)\:\mathrm{and}\:\mathrm{the}\:\mathrm{radius} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{1}\:\mathrm{when}\:\mathrm{P}\:\mathrm{remove}\:\mathrm{on}\:\left(\mathrm{O},\mathrm{2}\right) \\ $$
Commented by peter frank last updated on 05/Oct/20
$$\mathrm{thank}\:\mathrm{you} \\ $$