Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 109343 by 150505R last updated on 22/Aug/20

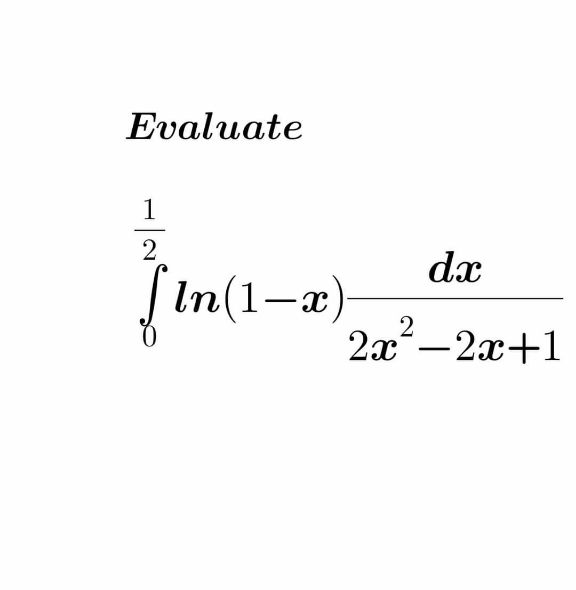
Commented by 150505R last updated on 22/Aug/20

$p l e a s e s o l v e$
	Answered by mathmax by abdo last updated on 23/Aug/20
	$A =∫_0 ^(1/2) ((ln(1−x))/(2x^2 −2x +1))dx ⇒A =_(x=(t/2)) ∫_0 ^1 ((ln(1−(t/2)))/(2((t^2 /4))−2((t/2))+1))(dt/2) =∫_0 ^1 ((ln(2−t))/(2{ (t^2 /2)−t +1})) dt =∫_0 ^1 ((ln(2−t))/(t^2 −2t +2)) dt =_(t=1−u) ∫_1 ^0 ((ln(2−1+u))/((1−u)^2 −2(1−u) +2))(−du) =∫_0 ^1 ((ln(1+u))/(u^2 −2u+1−2+2u +2)) du =∫_0 ^1 ((ln(1+u))/(1+u^2 )) du =_(u=tanθ) ∫_0 ^(π/4) ((ln(1+tanθ))/(1+tan^2 θ)) (1+tan^2 θ)dθ =∫_0 ^(π/4) ln(1+((sinθ)/(cosθ)))dθ =∫_0 ^(π/4) ln(cosθ +sinθ)dθ−∫_0 ^(π/4) ln(cosθ)dθ and all those integrals are known in the platform )i dont remember the values)....$
	$A = \int_{0}^{\frac{1}{2}} \frac{\ln (1 - x)}{{2 x}^{2} - 2 x + 1} dx \Rightarrow A =_{x = \frac{t}{2}} \int_{0}^{1} \frac{\ln (1 - \frac{t}{2})}{2 (\frac{t^{2}}{4}) - 2 (\frac{t}{2}) + 1} \frac{dt}{2}$ $= \int_{0}^{1} \frac{\ln (2 - t)}{2 {\frac{t^{2}}{2} - t + 1}} dt = \int_{0}^{1} \frac{\ln (2 - t)}{t^{2} - 2 t + 2} dt$ $=_{t = 1 - u} \int_{1}^{0} \frac{\ln (2 - 1 + u)}{{(1 - u)}^{2} - 2 (1 - u) + 2} (- du)$ $= \int_{0}^{1} \frac{\ln (1 + u)}{u^{2} - 2 u + 1 - 2 + 2 u + 2} du = \int_{0}^{1} \frac{\ln (1 + u)}{1 + u^{2}} du$ $=_{u = \tan θ} \int_{0}^{\frac{π}{4}} \frac{\ln (1 + \tan θ)}{1 + \tan^{2} θ} (1 + \tan^{2} θ) d θ$ $= \int_{0}^{\frac{π}{4}} \ln (1 + \frac{\sin θ}{\cos θ}) d θ = \int_{0}^{\frac{π}{4}} \ln (\cos θ + \sin θ) d θ - \int_{0}^{\frac{π}{4}} \ln (\cos θ) d θ$ $and all those integrals are known in the platform$ $) i dont remember the values) . . . .$
	Answered by mathdave last updated on 22/Aug/20

	$m y s o l u t i o n h e r e i t g o e s$ $I = \int_{0}^{\frac{1}{2}} \frac{\ln (1 - x)}{(2 x^{2} - 2 x + 1)} d x = \frac{2}{2} \int_{0}^{\frac{1}{2}} \frac{\ln (1 - x)}{(2 x^{2} - 2 x + 1)} d x = 2 \int_{0}^{\frac{1}{2}} \frac{\ln (1 - x)}{(4 x^{2} - 4 x + 2)} d x$ $I = 2 \int_{0}^{\frac{1}{2}} \frac{\ln (1 - x)}{{(2 x - 1)}^{2} + 1} d x (l e t 2 x - 1 = y a n d d x = \frac{d y}{2})$ $I = \frac{2}{2} \int_{- 1}^{0} \frac{\ln (1 - (\frac{1 + y}{2}))}{y^{2} + 1} d y = \int_{- 1}^{0} \frac{\ln (\frac{1 - y}{2})}{1 + y^{2}} d y$ $l e t y = - t d y = - d t$ $I = \int_{1}^{0} \frac{\ln (\frac{1 + t}{2})}{1 + t^{2}} \times - d t = \int_{0}^{1} \frac{\ln (1 + t)}{1 + t^{2}} d t - \int_{0}^{1} \frac{\ln 2}{1 + t^{2}} d t$ $I = \int_{0}^{1} \frac{\ln (1 + t)}{1 + t^{2}} d t - \ln 2 {[\tan^{- 1} (t)]}_{0}^{1} = \int_{0}^{1} \frac{\ln (1 + t)}{1 + t^{2}} d t - \frac{π}{4} \ln 2$ $l e t \tan x = t a n d d t = se c^{2} x d x a n d$ $1 + \tan^{2} x = \sec^{2} x$ $I = \int_{0}^{\frac{π}{4}} \frac{\ln (1 + \tan x)}{\sec^{2} x} \times \sec^{2} x d x - \frac{π}{4} \ln 2 = \int_{0}^{\frac{π}{4}} \ln (1 + \frac{\sin x}{\cos x}) d x - \frac{π}{4} \ln 2$ $I = \int_{0}^{\frac{π}{4}} \ln (\frac{\sin x + \cos x}{\cos x}) d x - \frac{π}{4} \ln 2 = \int_{0}^{\frac{π}{4}} \ln (\cos x + \sin x) d x - \int_{0}^{\frac{π}{4}} \ln (\cos x) d x - \frac{π}{4} \ln 2$ $s i n c e \int_{0}^{\frac{π}{2}} \ln (\cos x + \sin x) d x = G - \frac{π}{4} \ln 2$ $∵ \int_{0}^{\frac{π}{4}} \ln (\cos x + \sin x) d x = \frac{1}{2} \int_{0}^{\frac{π}{2}} \ln (\cos x + \sin x) d x = \frac{1}{2} (G - \frac{π}{4} \ln 2)$ $a n d \int_{0}^{\frac{π}{4}} \ln (\cos x) d x = \frac{G}{2} - \frac{π}{4} \ln 2 w h e n u d i n g t h i s$ $i d e n t i t y o f$ $\ln (\cos x) = - \ln 2 + \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n + 1} \cos (2 n x)}{n} f r o m$ $f o u r i e r s e r i e s$ $∵ I = \frac{G}{2} - \frac{π}{8} \ln 2 - [\frac{G}{2} - \frac{π}{4} \ln 2] - \frac{π}{4} \ln 2$ $I = \frac{G}{2} - \frac{G}{2} - \frac{π}{8} \ln 2 + \frac{π}{4} \ln 2 - \frac{π}{4} \ln 2 = - \frac{π}{8} \ln 2$ $∵ \int_{0}^{\frac{1}{2}} \frac{\ln (1 - x)}{2 x^{2} - 2 x + 1} d x = - \frac{π}{8} \ln 2$ $b y m a t h d a v e (22 / 08 / 2020)$
	Commented by mnjuly1970 last updated on 23/Aug/20

	$s i r . t i k a l l a m o b a r i n a m t i$ $f a r g h s a r m a n b e s h a s h a m . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum