
Question and Answers Forum
Question Number 109403 by abony1303 last updated on 23/Aug/20
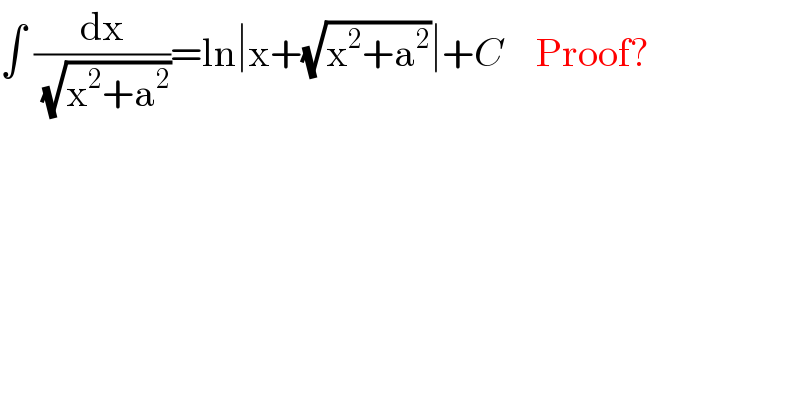
Answered by bobhans last updated on 23/Aug/20
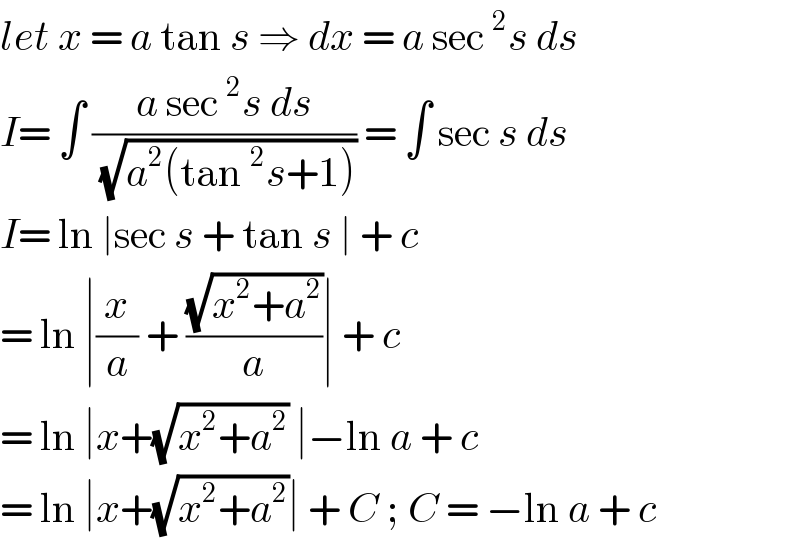
Answered by 1549442205PVT last updated on 23/Aug/20
![Since ∣x+(√(x^2 +a^2 )) ∣=x+(√(x^2 +a^2 )) (due to x+(√(x^2 +a^2 )) >0 ∀x∈R),so we have (d/dx)(ln∣x+(√(x^2 +a^2 ))∣+C)=(d/dx)[ln(x+(√(x^2 +a^2 )))] =(1/(x+(√(x^2 +a^2 ))))×(d/dx)(x+(√(x^2 +a^2 )) )= =(1/(x+(√(x^2 +a^2 ))))×(1+(x/( (√(x^2 +a^2 ))))) =(1/(x+(√(x^2 +a^2 ))))×((x+(√(x^2 +a^2 )))/( (√(x^2 +a^2 ))))=(1/( (√(x^2 +a^2 )))) This shows that ∫(dx/( (√(x^2 +a^2 ))))=ln∣x+(√(x^2 +a^2 ))∣+C (Q.E.D)](Q109438.png)
| ||
Question and Answers Forum | ||
Question Number 109403 by abony1303 last updated on 23/Aug/20 | ||
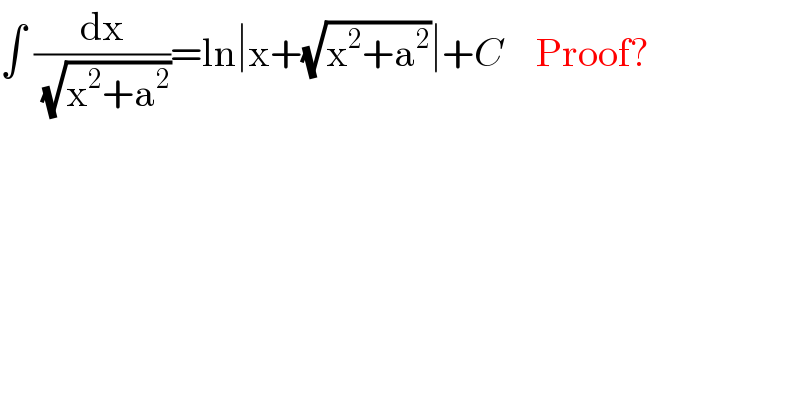 | ||
Answered by bobhans last updated on 23/Aug/20 | ||
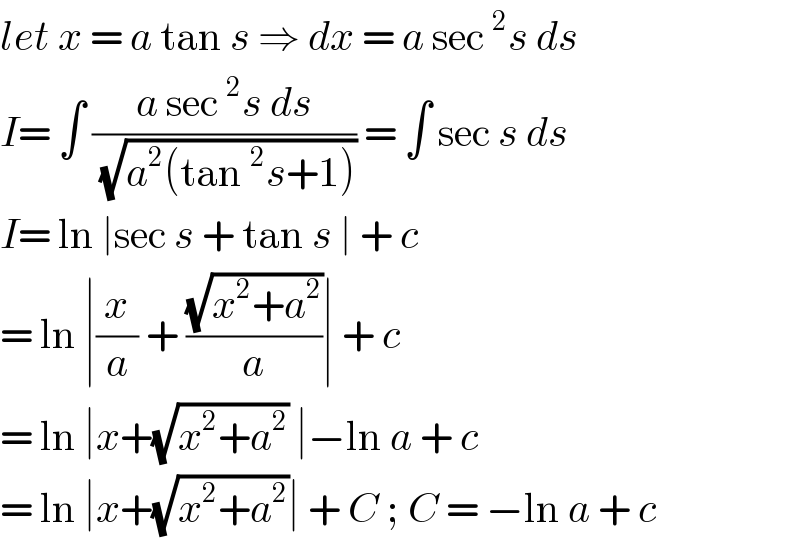 | ||
| ||
Answered by 1549442205PVT last updated on 23/Aug/20 | ||
![Since ∣x+(√(x^2 +a^2 )) ∣=x+(√(x^2 +a^2 )) (due to x+(√(x^2 +a^2 )) >0 ∀x∈R),so we have (d/dx)(ln∣x+(√(x^2 +a^2 ))∣+C)=(d/dx)[ln(x+(√(x^2 +a^2 )))] =(1/(x+(√(x^2 +a^2 ))))×(d/dx)(x+(√(x^2 +a^2 )) )= =(1/(x+(√(x^2 +a^2 ))))×(1+(x/( (√(x^2 +a^2 ))))) =(1/(x+(√(x^2 +a^2 ))))×((x+(√(x^2 +a^2 )))/( (√(x^2 +a^2 ))))=(1/( (√(x^2 +a^2 )))) This shows that ∫(dx/( (√(x^2 +a^2 ))))=ln∣x+(√(x^2 +a^2 ))∣+C (Q.E.D)](Q109438.png) | ||
| ||