Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 10944 by 314159 last updated on 03/Mar/17

Find all ordered pairs (a,b) so that ((ab)/(a+b)) is an integer. (a and b are integers).

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{ordered}\:\mathrm{pairs}\:\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{so}\:\mathrm{that}\:\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{b}}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer}. \\ $$$$\left(\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{are}\:\mathrm{integers}\right). \\ $$

Commented by FilupS last updated on 03/Mar/17

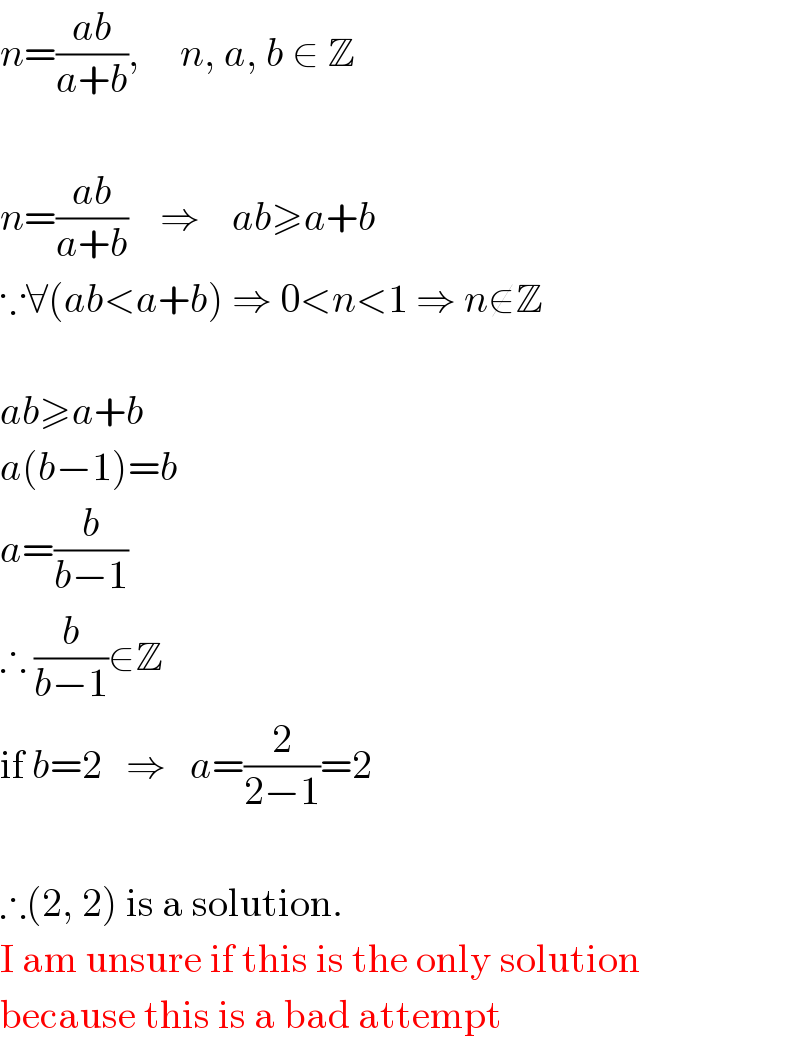
n=((ab)/(a+b)), n, a, b ∈ Z n=((ab)/(a+b)) ⇒ ab≥a+b ∵∀(ab<a+b) ⇒ 0<n<1 ⇒ n∉Z ab≥a+b a(b−1)=b a=(b/(b−1)) ∴ (b/(b−1))∈Z if b=2 ⇒ a=(2/(2−1))=2 ∴(2, 2) is a solution. I am unsure if this is the only solution because this is a bad attempt

$${n}=\frac{{ab}}{{a}+{b}},\:\:\:\:\:{n},\:{a},\:{b}\:\in\:\mathbb{Z} \\ $$$$\: \\ $$$${n}=\frac{{ab}}{{a}+{b}}\:\:\:\:\Rightarrow\:\:\:\:{ab}\geqslant{a}+{b} \\ $$$$\because\forall\left({ab}<{a}+{b}\right)\:\Rightarrow\:\mathrm{0}<{n}<\mathrm{1}\:\Rightarrow\:{n}\notin\mathbb{Z} \\ $$$$\: \\ $$$${ab}\geqslant{a}+{b} \\ $$$${a}\left({b}−\mathrm{1}\right)={b} \\ $$$${a}=\frac{{b}}{{b}−\mathrm{1}} \\ $$$$\therefore\:\frac{{b}}{{b}−\mathrm{1}}\in\mathbb{Z} \\ $$$$\mathrm{if}\:{b}=\mathrm{2}\:\:\:\Rightarrow\:\:\:{a}=\frac{\mathrm{2}}{\mathrm{2}−\mathrm{1}}=\mathrm{2} \\ $$$$\: \\ $$$$\therefore\left(\mathrm{2},\:\mathrm{2}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution} \\ $$$$\mathrm{because}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{bad}\:\mathrm{attempt} \\ $$

Commented by mrW1 last updated on 04/Mar/17

i think there should be infinite number pairs: 2/2 3/6 4/4 4/12 5/20 6/6 6/12 6/30 7/42 8/8 8/24 8/56 9/18 9/72 10/10 10/15 10/40 11/110 12/12 12/24 12/36 12/60 12/132 13/156 14/14 14/84 14/182 ......

$${i}\:{think}\:{there}\:{should}\:{be}\:{infinite}\:{number}\:{pairs}: \\ $$$$\mathrm{2}/\mathrm{2} \\ $$$$\mathrm{3}/\mathrm{6} \\ $$$$\mathrm{4}/\mathrm{4}\:\:\:\:\mathrm{4}/\mathrm{12} \\ $$$$\mathrm{5}/\mathrm{20} \\ $$$$\mathrm{6}/\mathrm{6}\:\:\:\:\mathrm{6}/\mathrm{12}\:\:\:\:\mathrm{6}/\mathrm{30} \\ $$$$\mathrm{7}/\mathrm{42} \\ $$$$\mathrm{8}/\mathrm{8}\:\:\:\:\mathrm{8}/\mathrm{24}\:\:\:\:\mathrm{8}/\mathrm{56} \\ $$$$\mathrm{9}/\mathrm{18}\:\:\:\:\mathrm{9}/\mathrm{72} \\ $$$$\mathrm{10}/\mathrm{10}\:\:\:\:\mathrm{10}/\mathrm{15}\:\:\:\:\mathrm{10}/\mathrm{40} \\ $$$$\mathrm{11}/\mathrm{110} \\ $$$$\mathrm{12}/\mathrm{12}\:\:\:\:\mathrm{12}/\mathrm{24}\:\:\:\:\mathrm{12}/\mathrm{36}\:\:\:\:\mathrm{12}/\mathrm{60}\:\:\:\mathrm{12}/\mathrm{132} \\ $$$$\mathrm{13}/\mathrm{156} \\ $$$$\mathrm{14}/\mathrm{14}\:\:\:\:\mathrm{14}/\mathrm{84}\:\:\:\:\mathrm{14}/\mathrm{182} \\ $$$$...... \\ $$

Answered by mrW1 last updated on 04/Mar/17

let ((ab)/(a+b))=n let b≥a and b=ka (k≥1) ⇒((aka)/((1+k)a))=n a=((1+k)/k)×n=n+(n/k) with (n/k)=i or k=(n/i) ⇒a=n+i b=ka=(n/i)(n+i)=n(1+(n/i)) with (n/i)=j or n=ji ⇒a=n+i=ji+i=(1+j)i ⇒b=n(1+j)=j(1+j)i i.e. the solution is { ((a=(1+j)i)),((b=j(1+j)i)) :} i,j∈N e.g. i=1, j=1,2,3,4... a/b=2/2, 3/6, 4/12, 5/20, 6/30...... i=2, j=1,2,3,4... a/b=4/4, 6/12, 8/24, 10/40, 12/60...... i=3, j=1,2,3,4... a/b=6/6, 9/18, 12/36, 15/60, 18/90...... ..... We see in the solution that a is the product of 2 numbers and b is the product of 3 numbers and b=a×j. For every a ≥2, if a is a prime number, there is one corresponding value for b, and if a is no prime number, there are two or more corresponding values for b. E.g. a=7 (prime number) which can only be expressed as 7×1 (j=6) ⇒there is only one value for b: b=7×6=42 E.g. a=12 which can be expressed as 12×1 (j=11) 3×4 (j=2) 4×3 (j=3) 2×6 (j=1) 6×2 (j=5) ⇒there are 5 values for b: b=12×1=12 b=12×2=24 b=12×3=36 b=12×5=60 b=12×11=132 the pairs of a and b for a from 2 till 14 see comment above.

$${let}\:\frac{{ab}}{{a}+{b}}={n} \\ $$$${let}\:{b}\geqslant{a}\:{and}\:{b}={ka}\:\left({k}\geqslant\mathrm{1}\right) \\ $$$$\Rightarrow\frac{{aka}}{\left(\mathrm{1}+{k}\right){a}}={n} \\ $$$${a}=\frac{\mathrm{1}+{k}}{{k}}×{n}={n}+\frac{{n}}{{k}} \\ $$$${with}\:\frac{{n}}{{k}}={i}\:{or}\:{k}=\frac{{n}}{{i}} \\ $$$$\Rightarrow{a}={n}+{i} \\ $$$${b}={ka}=\frac{{n}}{{i}}\left({n}+{i}\right)={n}\left(\mathrm{1}+\frac{{n}}{{i}}\right) \\ $$$${with}\:\frac{{n}}{{i}}={j}\:{or}\:{n}={ji} \\ $$$$\Rightarrow{a}={n}+{i}={ji}+{i}=\left(\mathrm{1}+{j}\right){i} \\ $$$$\Rightarrow{b}={n}\left(\mathrm{1}+{j}\right)={j}\left(\mathrm{1}+{j}\right){i} \\ $$$$ \\ $$$${i}.{e}.\:{the}\:{solution}\:{is} \\ $$$$\begin{cases}{{a}=\left(\mathrm{1}+{j}\right){i}}\\{{b}={j}\left(\mathrm{1}+{j}\right){i}}\end{cases} \\ $$$${i},{j}\in\mathbb{N} \\ $$$$ \\ $$$${e}.{g}. \\ $$$${i}=\mathrm{1},\:{j}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}... \\ $$$${a}/{b}=\mathrm{2}/\mathrm{2},\:\mathrm{3}/\mathrm{6},\:\mathrm{4}/\mathrm{12},\:\mathrm{5}/\mathrm{20},\:\mathrm{6}/\mathrm{30}...... \\ $$$$ \\ $$$${i}=\mathrm{2},\:{j}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}... \\ $$$${a}/{b}=\mathrm{4}/\mathrm{4},\:\mathrm{6}/\mathrm{12},\:\mathrm{8}/\mathrm{24},\:\mathrm{10}/\mathrm{40},\:\mathrm{12}/\mathrm{60}...... \\ $$$$ \\ $$$${i}=\mathrm{3},\:{j}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}... \\ $$$${a}/{b}=\mathrm{6}/\mathrm{6},\:\mathrm{9}/\mathrm{18},\:\mathrm{12}/\mathrm{36},\:\mathrm{15}/\mathrm{60},\:\mathrm{18}/\mathrm{90}...... \\ $$$$..... \\ $$$$ \\ $$$${We}\:{see}\:{in}\:{the}\:{solution}\:{that}\:{a}\:{is}\:{the} \\ $$$${product}\:{of}\:\mathrm{2}\:{numbers}\:{and}\:{b}\:{is}\:{the} \\ $$$${product}\:{of}\:\mathrm{3}\:{numbers}\:{and}\:{b}={a}×{j}. \\ $$$$ \\ $$$${For}\:{every}\:{a}\:\geqslant\mathrm{2},\: \\ $$$${if}\:{a}\:{is}\:{a}\:{prime}\:{number},\:{there}\:{is}\:{one} \\ $$$${corresponding}\:{value}\:{for}\:{b},\:{and} \\ $$$${if}\:{a}\:{is}\:{no}\:{prime}\:{number},\:{there}\:{are}\:{two} \\ $$$${or}\:{more}\:{corresponding}\:{values}\:{for}\:{b}. \\ $$$$ \\ $$$${E}.{g}.\:{a}=\mathrm{7}\:\left({prime}\:{number}\right)\:{which}\:{can} \\ $$$${only}\:{be}\:{expressed}\:{as} \\ $$$$\mathrm{7}×\mathrm{1}\:\:\:\left({j}=\mathrm{6}\right) \\ $$$$\Rightarrow{there}\:{is}\:{only}\:{one}\:{value}\:{for}\:{b}: \\ $$$${b}=\mathrm{7}×\mathrm{6}=\mathrm{42} \\ $$$$ \\ $$$${E}.{g}.\:{a}=\mathrm{12}\:{which}\:{can}\:{be}\:{expressed}\:{as} \\ $$$$\mathrm{12}×\mathrm{1}\:\:\left({j}=\mathrm{11}\right) \\ $$$$\mathrm{3}×\mathrm{4}\:\:\:\left({j}=\mathrm{2}\right) \\ $$$$\mathrm{4}×\mathrm{3}\:\:\:\left({j}=\mathrm{3}\right) \\ $$$$\mathrm{2}×\mathrm{6}\:\:\:\left({j}=\mathrm{1}\right) \\ $$$$\mathrm{6}×\mathrm{2}\:\:\:\left({j}=\mathrm{5}\right) \\ $$$$\Rightarrow{there}\:{are}\:\mathrm{5}\:{values}\:{for}\:{b}: \\ $$$${b}=\mathrm{12}×\mathrm{1}=\mathrm{12} \\ $$$${b}=\mathrm{12}×\mathrm{2}=\mathrm{24} \\ $$$${b}=\mathrm{12}×\mathrm{3}=\mathrm{36} \\ $$$${b}=\mathrm{12}×\mathrm{5}=\mathrm{60} \\ $$$${b}=\mathrm{12}×\mathrm{11}=\mathrm{132} \\ $$$$ \\ $$$${the}\:{pairs}\:{of}\:{a}\:{and}\:{b}\:{for}\:{a}\:{from}\:\mathrm{2}\:{till}\:\mathrm{14} \\ $$$${see}\:{comment}\:{above}. \\ $$

Commented by FilupS last updated on 04/Mar/17

I Tried a slimilar subtitution, but couldnt work with it.Awesome job

$$\mathrm{I}\:\mathrm{Tried}\:\mathrm{a}\:\mathrm{slimilar}\:\mathrm{subtitution},\:\mathrm{but}\:\mathrm{couldnt} \\ $$$$\mathrm{work}\:\mathrm{with}\:\mathrm{it}.\mathrm{Awesome}\:\mathrm{job} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com