
Question and Answers Forum
Question Number 109546 by bemath last updated on 24/Aug/20
![If f(x) continue in [ 1,30] and ∫_6 ^(30) f(x)dx = 30, then ∫_1 ^9 f(3y+3)dy = __](Q109546.png)
Commented by kaivan.ahmadi last updated on 24/Aug/20

Commented by bemath last updated on 24/Aug/20

Answered by 1549442205PVT last updated on 24/Aug/20
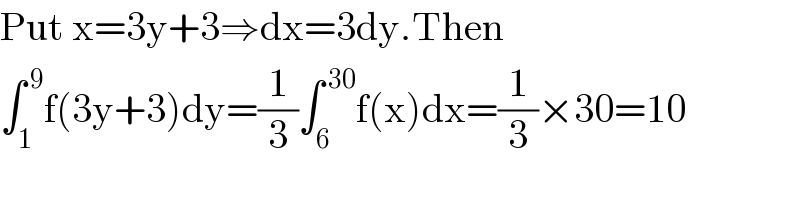
| ||
Question and Answers Forum | ||
Question Number 109546 by bemath last updated on 24/Aug/20 | ||
![If f(x) continue in [ 1,30] and ∫_6 ^(30) f(x)dx = 30, then ∫_1 ^9 f(3y+3)dy = __](Q109546.png) | ||
Commented by kaivan.ahmadi last updated on 24/Aug/20 | ||
 | ||
Commented by bemath last updated on 24/Aug/20 | ||
 | ||
Answered by 1549442205PVT last updated on 24/Aug/20 | ||
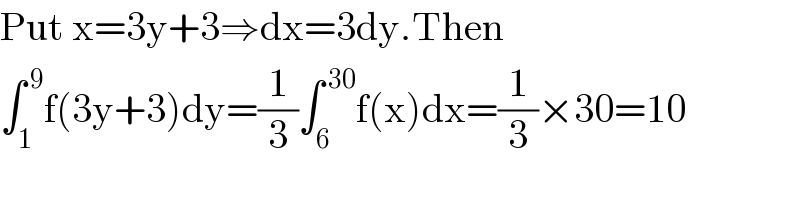 | ||
| ||