Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 109584 by bobhans last updated on 24/Aug/20

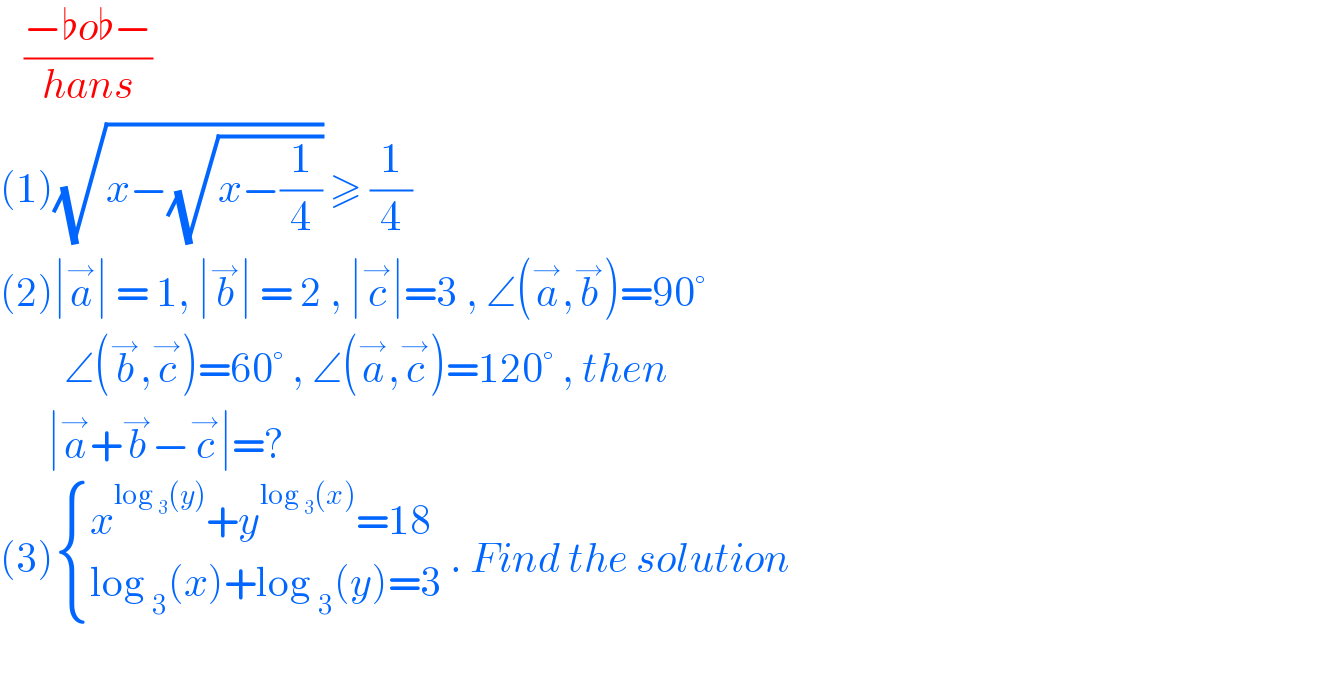
((−♭o♭−)/(hans)) (1)(√(x−(√(x−(1/4))))) ≥ (1/4) (2)∣a^→ ∣ = 1, ∣b^→ ∣ = 2 , ∣c^→ ∣=3 , ∠(a^→ ,b^→ )=90° ∠(b^→ ,c^→ )=60° , ∠(a^→ ,c^→ )=120° , then ∣a^→ +b^→ −c^→ ∣=? (3) { ((x^(log _3 (y)) +y^(log _3 (x)) =18)),((log _3 (x)+log _3 (y)=3)) :} . Find the solution

$$\:\:\:\frac{−\flat{o}\flat−}{{hans}} \\ $$$$\left(\mathrm{1}\right)\sqrt{{x}−\sqrt{{x}−\frac{\mathrm{1}}{\mathrm{4}}}}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\mid\overset{\rightarrow} {{a}}\mid\:=\:\mathrm{1},\:\mid\overset{\rightarrow} {{b}}\mid\:=\:\mathrm{2}\:,\:\mid\overset{\rightarrow} {{c}}\mid=\mathrm{3}\:,\:\angle\left(\overset{\rightarrow} {{a}},\overset{\rightarrow} {{b}}\right)=\mathrm{90}° \\ $$$$\:\:\:\:\:\:\:\:\angle\left(\overset{\rightarrow} {{b}},\overset{\rightarrow} {{c}}\right)=\mathrm{60}°\:,\:\angle\left(\overset{\rightarrow} {{a}},\overset{\rightarrow} {{c}}\right)=\mathrm{120}°\:,\:{then}\: \\ $$$$\:\:\:\:\:\:\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\mid=? \\ $$$$\left(\mathrm{3}\right)\begin{cases}{{x}^{\mathrm{log}\:_{\mathrm{3}} \left({y}\right)} +{y}^{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)} =\mathrm{18}}\\{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)+\mathrm{log}\:_{\mathrm{3}} \left({y}\right)=\mathrm{3}}\end{cases}\:.\:{Find}\:{the}\:{solution} \\ $$$$\:\:\: \\ $$

Commented by bemath last updated on 25/Aug/20

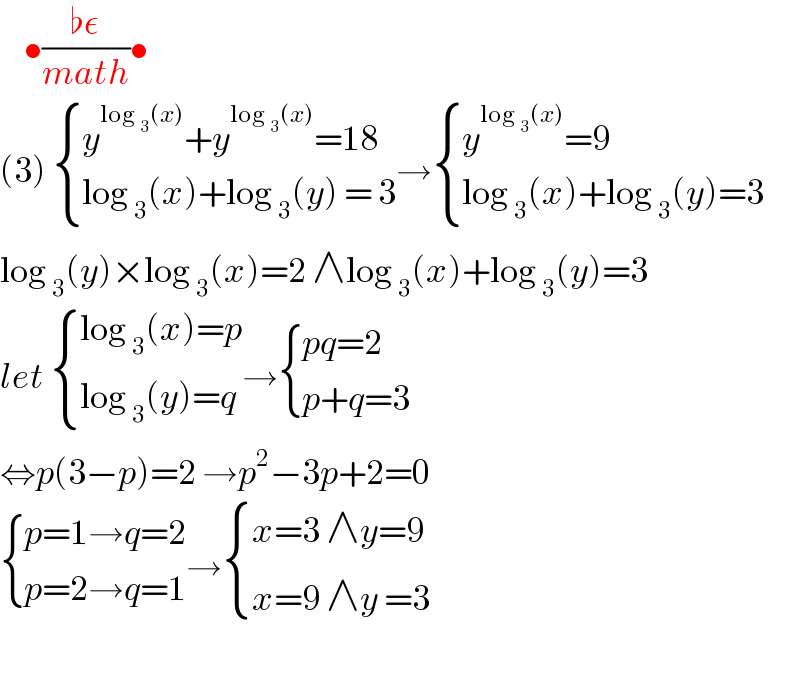
•((♭ε)/(math))• (3) { ((y^(log _3 (x)) +y^(log _3 (x)) =18)),((log _3 (x)+log _3 (y) = 3)) :}→ { ((y^(log _3 (x)) =9)),((log _3 (x)+log _3 (y)=3)) :} log _3 (y)×log _3 (x)=2 ∧log _3 (x)+log _3 (y)=3 let { ((log _3 (x)=p)),((log _3 (y)=q)) :}→ { ((pq=2)),((p+q=3)) :} ⇔p(3−p)=2 →p^2 −3p+2=0 { ((p=1→q=2)),((p=2→q=1)) :}→ { ((x=3 ∧y=9)),((x=9 ∧y =3)) :}

$$\:\:\:\:\bullet\frac{\flat\epsilon}{{math}}\bullet \\ $$$$\left(\mathrm{3}\right)\:\begin{cases}{{y}^{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)} +{y}^{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)} =\mathrm{18}}\\{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)+\mathrm{log}\:_{\mathrm{3}} \left({y}\right)\:=\:\mathrm{3}}\end{cases}\rightarrow\begin{cases}{{y}^{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)} =\mathrm{9}}\\{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)+\mathrm{log}\:_{\mathrm{3}} \left({y}\right)=\mathrm{3}}\end{cases} \\ $$$$\mathrm{log}\:_{\mathrm{3}} \left({y}\right)×\mathrm{log}\:_{\mathrm{3}} \left({x}\right)=\mathrm{2}\:\wedge\mathrm{log}\:_{\mathrm{3}} \left({x}\right)+\mathrm{log}\:_{\mathrm{3}} \left({y}\right)=\mathrm{3} \\ $$$${let}\:\begin{cases}{\mathrm{log}\:_{\mathrm{3}} \left({x}\right)={p}}\\{\mathrm{log}\:_{\mathrm{3}} \left({y}\right)={q}}\end{cases}\rightarrow\begin{cases}{{pq}=\mathrm{2}}\\{{p}+{q}=\mathrm{3}}\end{cases} \\ $$$$\Leftrightarrow{p}\left(\mathrm{3}−{p}\right)=\mathrm{2}\:\rightarrow{p}^{\mathrm{2}} −\mathrm{3}{p}+\mathrm{2}=\mathrm{0} \\ $$$$\begin{cases}{{p}=\mathrm{1}\rightarrow{q}=\mathrm{2}}\\{{p}=\mathrm{2}\rightarrow{q}=\mathrm{1}}\end{cases}\rightarrow\begin{cases}{{x}=\mathrm{3}\:\wedge{y}=\mathrm{9}}\\{{x}=\mathrm{9}\:\wedge{y}\:=\mathrm{3}}\end{cases} \\ $$$$ \\ $$

Answered by bemath last updated on 24/Aug/20

((↭♭ε↭)/(ΔMathΔ)) (2)consider a^→ .a^→ = ∣a^→ ∣^2 (a^→ +b^→ −c^→ )○(a^→ +b^→ −c^→ )= ∣a^→ +b^→ −c^→ ∣^2 ∣a^→ ∣^2 +2 a^→ ○b^→ −2 a^→ ○c^→ +∣b^→ ∣^2 −2 b^→ ○c^→ +∣c^→ ∣= ∣a^→ +b^→ −c^→ ∣^2 1+4+9+0−2(1)(3)(−(1/2))−2(2)(3)((1/2))= ∣a^→ +b^→ −c^→ ∣^2 14+3−6=∣a^→ +b^→ −c^→ ∣^2 ∴ ∣a^→ +b^→ −c^→ ∣ = (√(11))

$$\:\:\:\frac{\leftrightsquigarrow\flat\epsilon\leftrightsquigarrow}{\Delta\mathcal{M}{ath}\Delta} \\ $$$$\left(\mathrm{2}\right){consider}\:\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{a}}\:=\:\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} \\ $$$$\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\right)\circ\left(\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\right)=\:\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\mid^{\mathrm{2}} \\ $$$$\mid\overset{\rightarrow} {{a}}\mid^{\mathrm{2}} +\mathrm{2}\:\overset{\rightarrow} {{a}}\circ\overset{\rightarrow} {{b}}−\mathrm{2}\:\overset{\rightarrow} {{a}}\circ\overset{\rightarrow} {{c}}+\mid\overset{\rightarrow} {{b}}\mid^{\mathrm{2}} −\mathrm{2}\:\overset{\rightarrow} {{b}}\circ\overset{\rightarrow} {{c}}+\mid\overset{\rightarrow} {{c}}\mid= \\ $$$$\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\mid^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{4}+\mathrm{9}+\mathrm{0}−\mathrm{2}\left(\mathrm{1}\right)\left(\mathrm{3}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\left(\mathrm{2}\right)\left(\mathrm{3}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\mid^{\mathrm{2}} \\ $$$$\mathrm{14}+\mathrm{3}−\mathrm{6}=\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\mid^{\mathrm{2}} \\ $$$$\therefore\:\mid\overset{\rightarrow} {{a}}+\overset{\rightarrow} {{b}}−\overset{\rightarrow} {{c}}\mid\:=\:\sqrt{\mathrm{11}}\: \\ $$

Commented by bobhans last updated on 25/Aug/20

yeahh...

$${yeahh}... \\ $$

Answered by john santu last updated on 24/Aug/20

(√(x−(√(x−(1/4))))) ≥ (1/4) ⇒x−(√(x−(1/4))) ≥ (1/(16)) ⇒x−(1/(16)) ≥ (√(x−(1/4))) ; x > (1/(16)) (1) ⇒x^2 −(x/8)+(1/(256)) ≥x−(1/4) ⇒x^2 −((9x)/8)+((65)/(256)) ≥ 0 ⇒(x−(9/(16)))^2 −((81)/(256))+((65)/(256)) ≥ 0 ⇒(x−(9/(16)))^2 −((4/(16)))^2 ≥ 0 ⇒(x−((13)/(16)))(x−(5/(16)))≥0 ⇒x ≤ (5/(16)) ∪ x ≥ ((13)/(16)) (2) ⇒(√(x−(1/4))) define for x ≥ (4/(16)) (3) solution we get from (1)∩(2)∩(3) x ∈ [ (1/4), (5/(16)) ] ∪ [ ((13)/(16)) ,∞ )

$$\sqrt{{x}−\sqrt{{x}−\frac{\mathrm{1}}{\mathrm{4}}}}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{x}−\sqrt{{x}−\frac{\mathrm{1}}{\mathrm{4}}}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\Rightarrow{x}−\frac{\mathrm{1}}{\mathrm{16}}\:\geqslant\:\sqrt{{x}−\frac{\mathrm{1}}{\mathrm{4}}}\:;\:{x}\:>\:\frac{\mathrm{1}}{\mathrm{16}}\:\left(\mathrm{1}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\frac{{x}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{256}}\:\geqslant{x}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\frac{\mathrm{9}{x}}{\mathrm{8}}+\frac{\mathrm{65}}{\mathrm{256}}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{9}}{\mathrm{16}}\right)^{\mathrm{2}} −\frac{\mathrm{81}}{\mathrm{256}}+\frac{\mathrm{65}}{\mathrm{256}}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{9}}{\mathrm{16}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{4}}{\mathrm{16}}\right)^{\mathrm{2}} \geqslant\:\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{13}}{\mathrm{16}}\right)\left({x}−\frac{\mathrm{5}}{\mathrm{16}}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\:\leqslant\:\frac{\mathrm{5}}{\mathrm{16}}\:\cup\:{x}\:\geqslant\:\frac{\mathrm{13}}{\mathrm{16}}\:\left(\mathrm{2}\right) \\ $$$$\Rightarrow\sqrt{{x}−\frac{\mathrm{1}}{\mathrm{4}}}\:{define}\:{for}\:{x}\:\geqslant\:\frac{\mathrm{4}}{\mathrm{16}}\:\left(\mathrm{3}\right) \\ $$$${solution}\:{we}\:{get}\:{from}\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right)\cap\left(\mathrm{3}\right) \\ $$$${x}\:\in\:\left[\:\frac{\mathrm{1}}{\mathrm{4}},\:\frac{\mathrm{5}}{\mathrm{16}}\:\right]\:\cup\:\left[\:\frac{\mathrm{13}}{\mathrm{16}}\:,\infty\:\right) \\ $$

Commented by bobhans last updated on 25/Aug/20

yuhhuuyy

$${yuhhuuyy} \\ $$

Answered by 1549442205PVT last updated on 24/Aug/20

Solve the inequality (1)(√(x−(√(x−(1/4))))) ≥ (1/4) We need must have the condition that x≥(1/4) in order to define the root.Under this condition squaring two sides of the inequality we get an equivalent inequality x−(√(x−(1/4))) ≥(1/(16))⇔x−(1/(16))≥(√(x−(1/4))) Since both sides are positive,squaring again we get ⇔x^2 −(1/8)x+(1/(256))≥x−(1/4) ⇔256x^2 −288x+65≥0(2) Δ′=144^2 −256.65=16^2 .(9^2 −65)=16^3 (√Δ) =64,x_(1,2) =((144±64)/(256))∈{((13)/(16));(5/(16))} ⇒(2)⇔x∈(−∞;(5/(16))]∪[((13)/(16));+∞) Combining to the condition x≥(1/4) we get roots of given inequality be x∈[(1/4);(5/(16))]∪[((13)/(16));+∞) 2)∣a^(→) +b^(→) −c^(→) ∣^2 =a^2 +b^2 +c^2 +2a^(→) .b^(→) −2a^(→) .c^(→) −2b^(→) .c^(→) =1^2 +2^2 +3^2 +2∣a∣.∣b∣cos90° −2∣a∣.∣c∣cos120°−2∣b∣.∣c∣cos60° =14+2.1.2×0−2×1×3(−0.5) −2.2.3.0.5=14+3−6=11 Hence,∣a^(→) +b^(→) −c^(→) ∣=(√(11))

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{inequality} \\ $$$$\left(\mathrm{1}\right)\sqrt{{x}−\sqrt{{x}−\frac{\mathrm{1}}{\mathrm{4}}}}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{must}\:\mathrm{have}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{that} \\ $$$$\mathrm{x}\geqslant\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{in}\:\mathrm{order}\:\mathrm{to}\:\mathrm{define}\:\mathrm{the}\:\mathrm{root}.\mathrm{Under} \\ $$$$\mathrm{this}\:\mathrm{condition}\:\mathrm{squaring}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{inequality}\:\mathrm{we}\:\mathrm{get}\:\mathrm{an}\:\mathrm{equivalent} \\ $$$$\mathrm{inequality} \\ $$$$\mathrm{x}−\sqrt{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}}\:\geqslant\frac{\mathrm{1}}{\mathrm{16}}\Leftrightarrow\mathrm{x}−\frac{\mathrm{1}}{\mathrm{16}}\geqslant\sqrt{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{Since}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{are}\:\mathrm{positive},\mathrm{squaring} \\ $$$$\mathrm{again}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{256}}\geqslant\mathrm{x}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{256x}^{\mathrm{2}} −\mathrm{288x}+\mathrm{65}\geqslant\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\Delta'=\mathrm{144}^{\mathrm{2}} −\mathrm{256}.\mathrm{65}=\mathrm{16}^{\mathrm{2}} .\left(\mathrm{9}^{\mathrm{2}} −\mathrm{65}\right)=\mathrm{16}^{\mathrm{3}} \\ $$$$\sqrt{\Delta}\:=\mathrm{64},\mathrm{x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{144}\pm\mathrm{64}}{\mathrm{256}}\in\left\{\frac{\mathrm{13}}{\mathrm{16}};\frac{\mathrm{5}}{\mathrm{16}}\right\} \\ $$$$\Rightarrow\left(\mathrm{2}\right)\Leftrightarrow\mathrm{x}\in\left(−\infty;\frac{\mathrm{5}}{\mathrm{16}}\right]\cup\left[\frac{\mathrm{13}}{\mathrm{16}};+\infty\right) \\ $$$$\mathrm{Combining}\:\mathrm{to}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{x}\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{be} \\ $$$$\mathrm{x}\in\left[\frac{\mathrm{1}}{\mathrm{4}};\frac{\mathrm{5}}{\mathrm{16}}\right]\cup\left[\frac{\mathrm{13}}{\mathrm{16}};+\infty\right) \\ $$$$\left.\mathrm{2}\right)\mid\overset{\rightarrow} {\mathrm{a}}+\overset{\rightarrow} {\mathrm{b}}−\overset{\rightarrow} {\mathrm{c}}\mid^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{2}\overset{\rightarrow} {\mathrm{a}}.\overset{\rightarrow} {\mathrm{b}}−\mathrm{2}\overset{\rightarrow} {\mathrm{a}}.\overset{\rightarrow} {\mathrm{c}} \\ $$$$−\mathrm{2}\overset{\rightarrow} {\mathrm{b}}.\overset{\rightarrow} {\mathrm{c}}=\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{2}\mid\mathrm{a}\mid.\mid\mathrm{b}\mid\mathrm{cos90}° \\ $$$$−\mathrm{2}\mid\mathrm{a}\mid.\mid\mathrm{c}\mid\mathrm{cos120}°−\mathrm{2}\mid\mathrm{b}\mid.\mid\mathrm{c}\mid\mathrm{cos60}° \\ $$$$=\mathrm{14}+\mathrm{2}.\mathrm{1}.\mathrm{2}×\mathrm{0}−\mathrm{2}×\mathrm{1}×\mathrm{3}\left(−\mathrm{0}.\mathrm{5}\right) \\ $$$$−\mathrm{2}.\mathrm{2}.\mathrm{3}.\mathrm{0}.\mathrm{5}=\mathrm{14}+\mathrm{3}−\mathrm{6}=\mathrm{11} \\ $$$$\mathrm{Hence},\mid\overset{\rightarrow} {\mathrm{a}}+\overset{\rightarrow} {\mathrm{b}}−\overset{\rightarrow} {\mathrm{c}}\mid=\sqrt{\mathrm{11}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com