Math Question and Answers


Question and Answers Forum

All Questions Topic List
Limits Questions
Previous in All Question Next in All Question
Previous in Limits Next in Limits
Question Number 109639 by Ar Brandon last updated on 24/Aug/20

	Answered by Dwaipayan Shikari last updated on 25/Aug/20

	$S = \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n}}{n^{2}} = (- 1) \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n + 1}}{n^{2}} = (- 1) (\frac{1}{1} - \frac{1}{2^{2}} + \frac{1}{3^{2}} - \frac{1}{4^{2}} + . . . . .)$ $S_{n} = \underset{n = 1}{\sum^{\infty}} \frac{1}{n^{2}} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + . . . .$ $S_{n} - S = 2 (\frac{1}{2^{2}} + \frac{1}{4^{2}} + . . . .) = 2 \underset{n = 1}{\sum^{\infty}} \frac{1}{{(2 n)}^{2}}$ $\sum^{\infty} \frac{1}{n^{2}} - \sum^{\infty} \frac{1}{2 n^{2}} = S$ $\frac{1}{2} \sum^{\infty} \frac{1}{n^{2}} = S$ $\frac{1}{2} . \frac{π^{2}}{6} = S$ $S = \frac{π^{2}}{12}$ $S = - \frac{π^{2}}{12}$
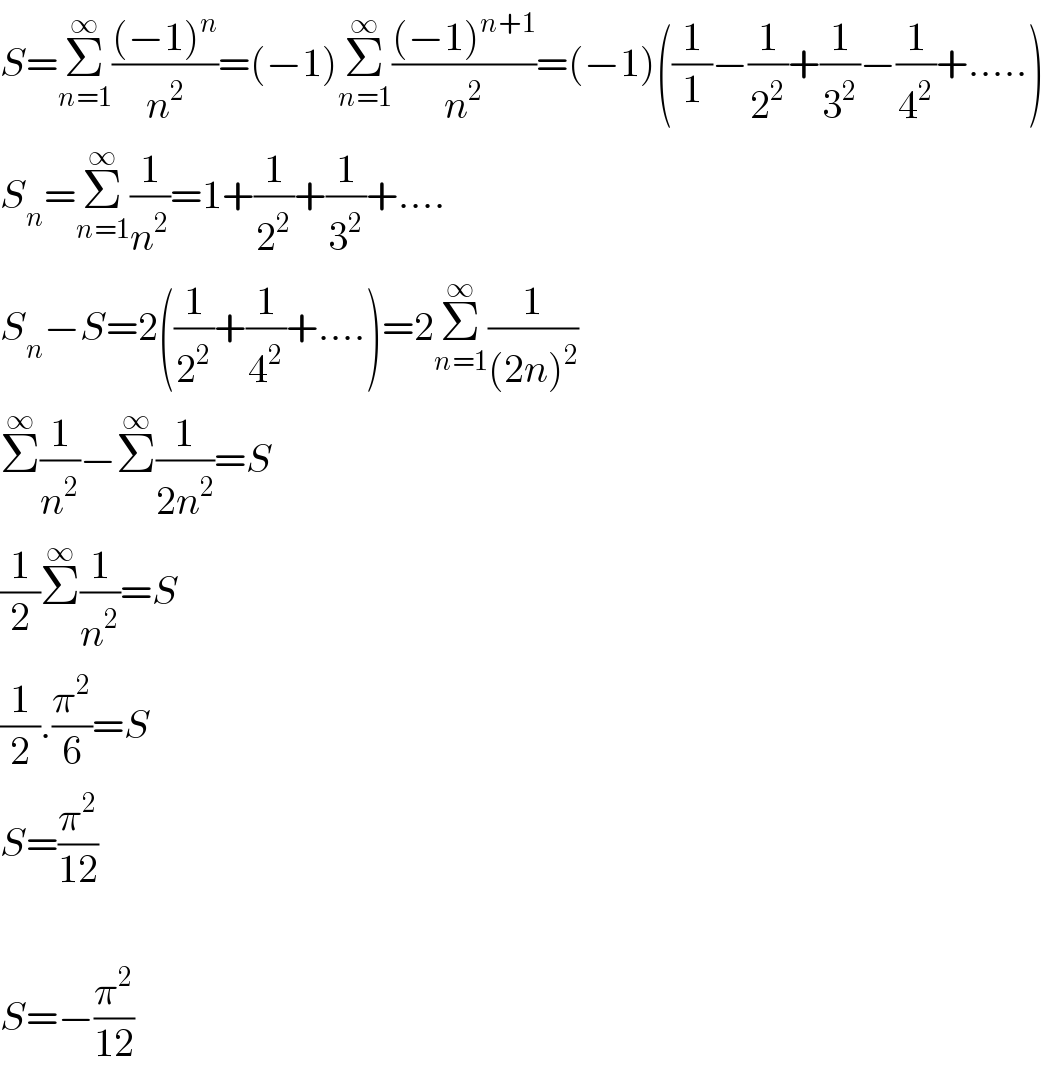
	Commented by mathmax by abdo last updated on 25/Aug/20

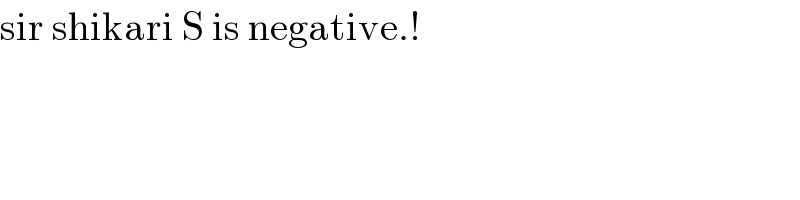
	$sir shikari S is negative .!$
	Answered by mathmax by abdo last updated on 25/Aug/20
	$1)f(x) =u(x)+v(x) with u(x)=x^2 (even) and v =πx(odd) u(x) =(a_o /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T)∫_([T]) u(x)cos(nx)dx =(1/π)∫_(−π) ^π x^2 cos(nx) =(2/π)∫_0 ^π x^2 cos(nx)dx ⇒ (π/2)a_n =[(x^2 /n)sin(nx)]_0 ^π −∫_0 ^π ((2x)/n) sin(nx)dx =−(2/n)∫_0 ^π xsin(nx)dx =−(2/n){ [−(x/n)cos(nx)]_0 ^π +∫_0 ^π (1/n)cos(nx)dx} =−(2/n){ −(π/n)(−1)^n +(1/n^2 )[sin(nx)]_0 ^π } =((2π)/n^2 )(−1)^(n ) ⇒ a_n =((2π)/n^2 )×(2/π)(−1)^n =(4/n^2 )(−1)^n we hsve a_o =(2/π)∫_0 ^π x^2 dx =(2/π)[(x^3 /3)]_0 ^π =(2/π)×(π^3 /3) =((2π^2 )/3) ⇒(a_o /2) =(π^2 /3) ⇒x^2 =(π^2 /3) +4Σ_(n=1) ^∞ (((−1)^n )/n^2 )cos(nx) v(x) =πx =Σ_(n=1) ^∞ b_n sin(nx) ⇒ b_n =(2/T)∫_([T]) v(x)sin(nx)dx =(1/π)∫_(−π) ^π πxsin(nx)dx =2 ∫_0 ^π x sin(nx)dx =2{ [−(x/n)cos(nx)]_0 ^π +∫_0 ^π (1/n)cos)nx)dx} =2{−(π/n)(−1)^n +(1/n^2 )[sin(nx)]_0 ^π } =((−2π)/n) (−1)^n ⇒ v(x) =πx =−2π Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx) ⇒ f(x) =(π^2 /3)+4Σ_(n=1) ^∞ (((−1)^n )/n^2 )cos(nx)−2π Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx) 2) x=0 ⇒0 =(π^2 /3) +4 Σ_(n=1) ^∞ (((−1)^n )/n^2 ) ⇒Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−(π^2 /(12))$
	$1) f (x) = u (x) + v (x) with u (x) = x^{2} (even) and v = π x (odd)$ $u (x) = \frac{a_{o}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (nx)$ $a_{n} = \frac{2}{T} \int_{[T]} u (x) \cos (nx) dx = \frac{1}{π} \int_{- π}^{π} x^{2} \cos (nx) = \frac{2}{π} \int_{0}^{π} x^{2} \cos (nx) dx \Rightarrow$ $\frac{π}{2} a_{n} = {[\frac{x^{2}}{n} \sin (nx)]}_{0}^{π} - \int_{0}^{π} \frac{2 x}{n} \sin (nx) dx = - \frac{2}{n} \int_{0}^{π} xsin (nx) dx$ $= - \frac{2}{n} {{[- \frac{x}{n} \cos (nx)]}_{0}^{π} + \int_{0}^{π} \frac{1}{n} \cos (nx) dx}$ $= - \frac{2}{n} {- \frac{π}{n} {(- 1)}^{n} + \frac{1}{n^{2}} {[\sin (nx)]}_{0}^{π}} = \frac{2 π}{n^{2}} {(- 1)}^{n} \Rightarrow$ $a_{n} = \frac{2 π}{n^{2}} \times \frac{2}{π} {(- 1)}^{n} = \frac{4}{n^{2}} {(- 1)}^{n} we hsve a_{o} = \frac{2}{π} \int_{0}^{π} x^{2} dx$ $= \frac{2}{π} {[\frac{x^{3}}{3}]}_{0}^{π} = \frac{2}{π} \times \frac{π^{3}}{3} = \frac{2 π^{2}}{3} \Rightarrow \frac{a_{o}}{2} = \frac{π^{2}}{3} \Rightarrow x^{2} = \frac{π^{2}}{3} + 4 \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n^{2}} \cos (nx)$ $v (x) = π x = \sum_{n = 1}^{\infty} b_{n} \sin (nx) \Rightarrow$ $b_{n} = \frac{2}{T} \int_{[T]} v (x) \sin (nx) dx = \frac{1}{π} \int_{- π}^{π} π xsin (nx) dx$ $= 2 \int_{0}^{π} x \sin (nx) dx = 2 {{[- \frac{x}{n} \cos (nx)]}_{0}^{π} + \int_{0}^{π} \frac{1}{n} \cos) nx) dx}$ $= 2 {- \frac{π}{n} {(- 1)}^{n} + \frac{1}{n^{2}} {[\sin (nx)]}_{0}^{π}} = \frac{- 2 π}{n} {(- 1)}^{n} \Rightarrow$ $v (x) = π x = - 2 π \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n} \sin (nx) \Rightarrow$ $f (x) = \frac{π^{2}}{3} + 4 \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n^{2}} \cos (nx) - 2 π \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n} \sin (nx)$ $2) x = 0 \Rightarrow 0 = \frac{π^{2}}{3} + 4 \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n^{2}} \Rightarrow \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n^{2}} = - \frac{π^{2}}{12}$
	Commented by Ar Brandon last updated on 25/Aug/20
	Je vous remercie��
	Commented by mathmax by abdo last updated on 25/Aug/20

	$you are welcome$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum