Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 109709 by nimnim last updated on 25/Aug/20

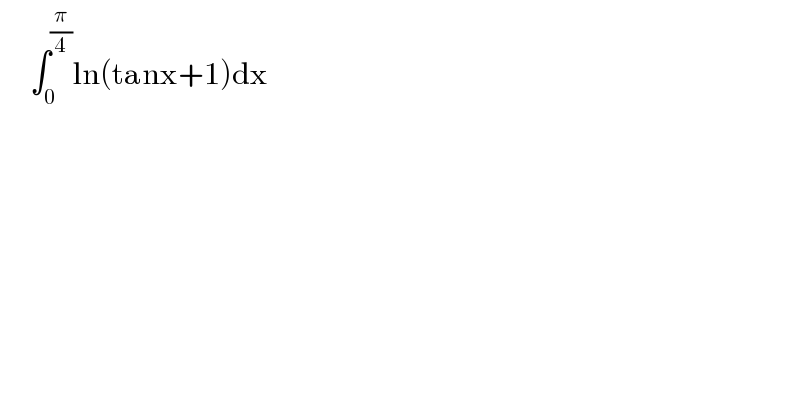
∫_(0 ) ^(π/4) ln(tanx+1)dx

$$\:\:\:\:\:\int_{\mathrm{0}\:} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{tanx}+\mathrm{1}\right)\mathrm{dx} \\ $$

Answered by mnjuly1970 last updated on 25/Aug/20

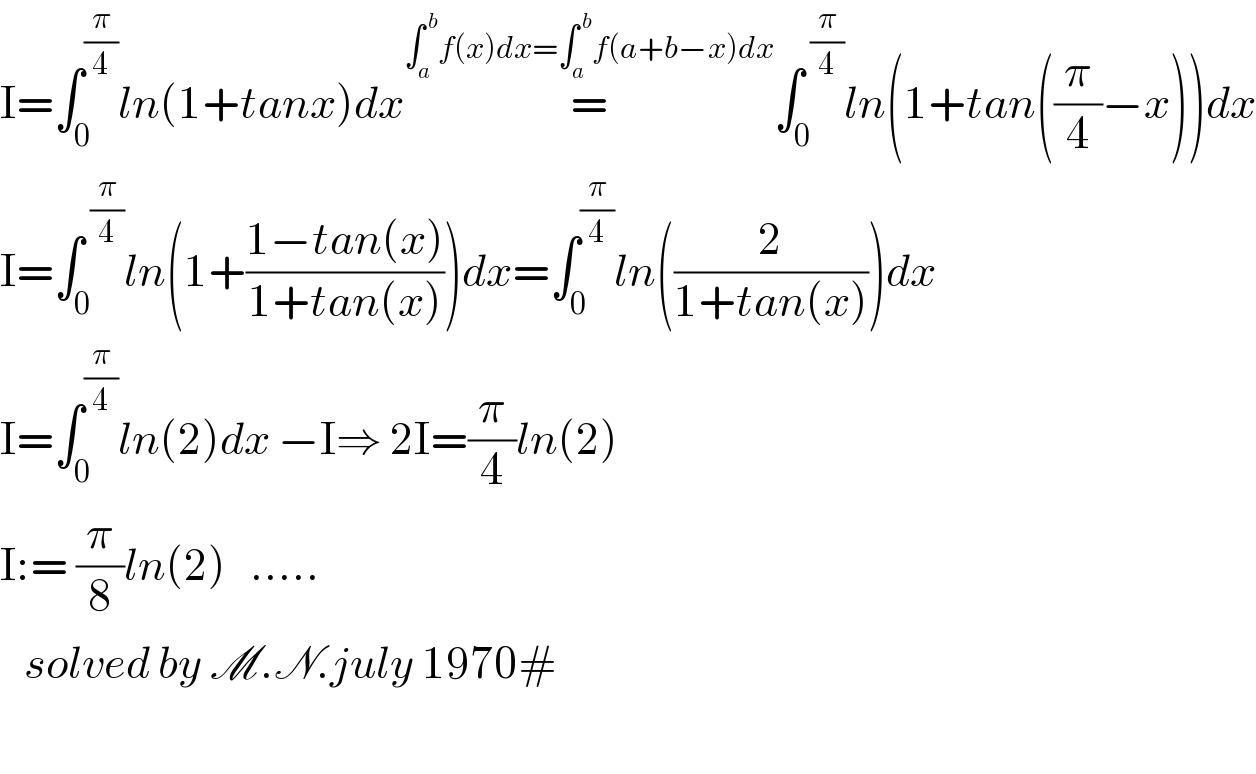
I=∫_0 ^(π/4) ln(1+tanx)dx=^(∫_a ^( b) f(x)dx=∫_a ^( b) f(a+b−x)dx) ∫_0 ^( (π/4)) ln(1+tan((π/4)−x))dx I=∫_0 ^( (π/4)) ln(1+((1−tan(x))/(1+tan(x))))dx=∫_0 ^(π/4) ln((2/(1+tan(x))))dx I=∫_0 ^(π/4) ln(2)dx −I⇒ 2I=(π/4)ln(2) I:= (π/8)ln(2) ..... solved by M.N.july 1970#

$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanx}\right){dx}\overset{\int_{{a}} ^{\:{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{\:{b}} {f}\left({a}+{b}−{x}\right){dx}} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\right){dx} \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tan}\left({x}\right)}{\mathrm{1}+{tan}\left({x}\right)}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tan}\left({x}\right)}\right){dx} \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{2}\right){dx}\:−\mathrm{I}\Rightarrow\:\mathrm{2I}=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{I}:=\:\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:\:\:.....\:\:\: \\ $$$$\:\:\:{solved}\:{by}\:\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}# \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 25/Aug/20

grateful..

$${grateful}.. \\ $$

Commented by nimnim last updated on 25/Aug/20

Thank you Sir.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$

Answered by mathmax by abdo last updated on 25/Aug/20

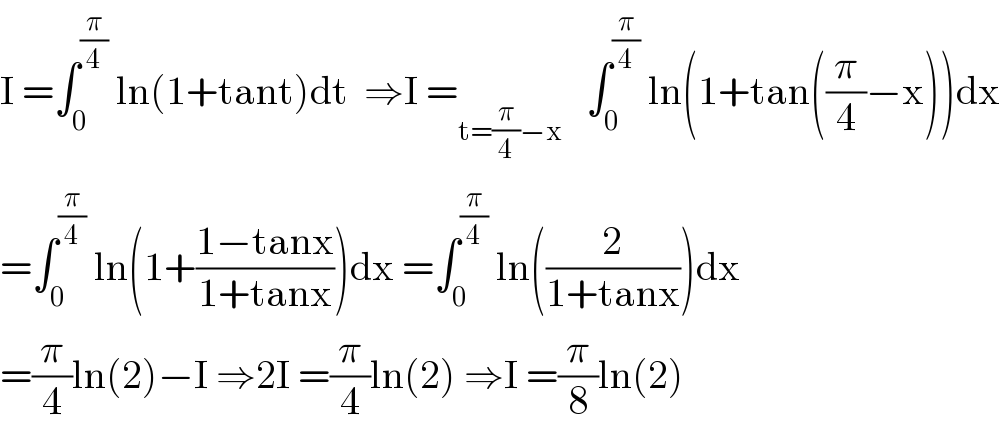
I =∫_0 ^(π/4) ln(1+tant)dt ⇒I =_(t=(π/4)−x) ∫_0 ^(π/4) ln(1+tan((π/4)−x))dx =∫_0 ^(π/4) ln(1+((1−tanx)/(1+tanx)))dx =∫_0 ^(π/4) ln((2/(1+tanx)))dx =(π/4)ln(2)−I ⇒2I =(π/4)ln(2) ⇒I =(π/8)ln(2)

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tant}\right)\mathrm{dt}\:\:\Rightarrow\mathrm{I}\:=_{\mathrm{t}=\frac{\pi}{\mathrm{4}}−\mathrm{x}} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{tanx}}{\mathrm{1}+\mathrm{tanx}}\right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tanx}}\right)\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{I}\:\Rightarrow\mathrm{2I}\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\mathrm{I}\:=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com