Question and Answers Forum
Question Number 109760 by ajfour last updated on 25/Aug/20
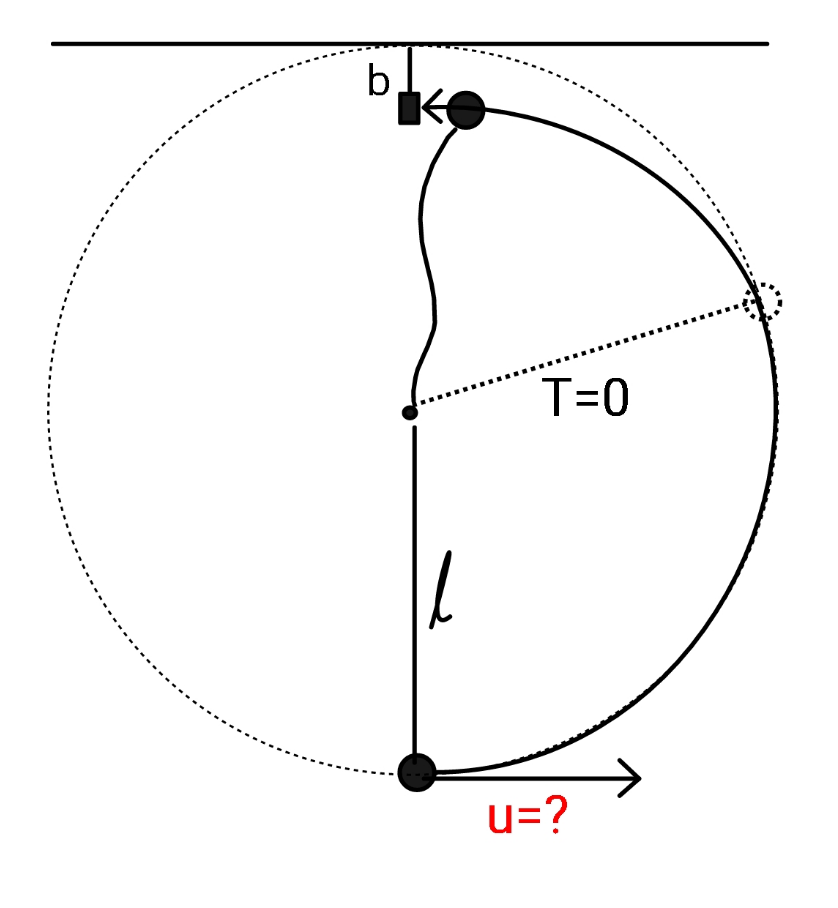
Commented by ajfour last updated on 25/Aug/20
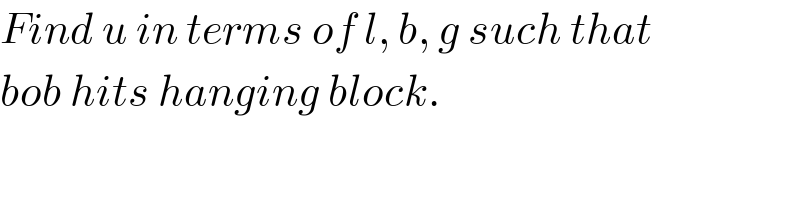
Answered by mr W last updated on 25/Aug/20
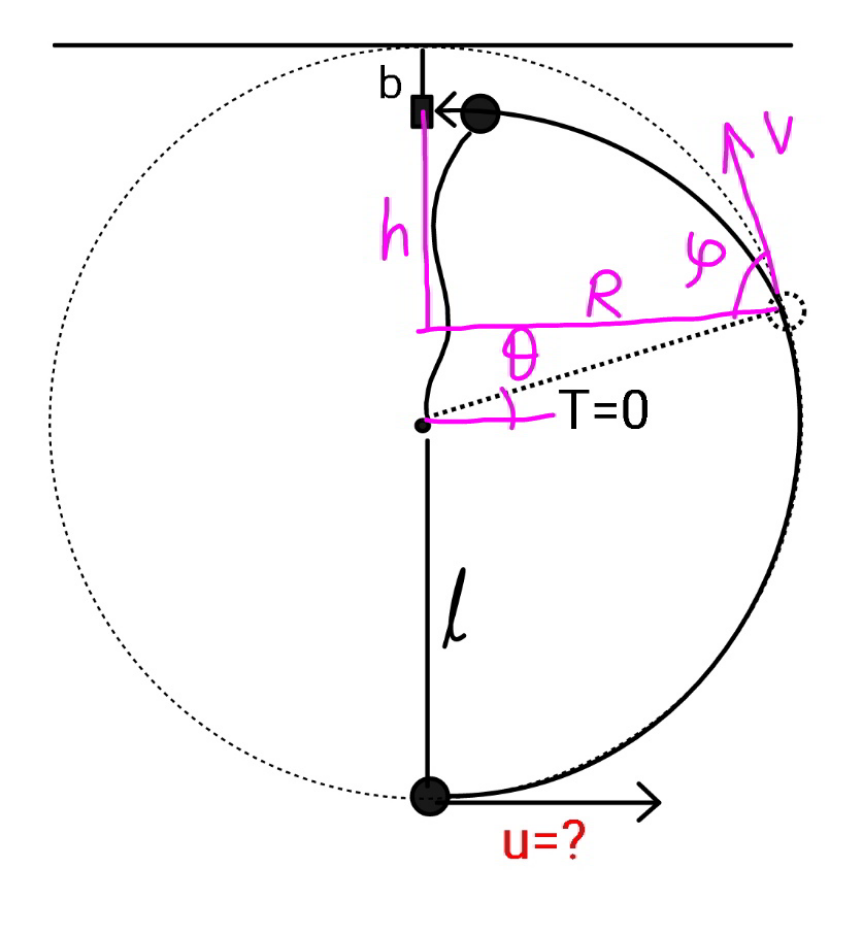
Commented by mr W last updated on 27/Aug/20
![(1/2)mv^2 +mgl(1+sin θ)=(1/2)mu^2 ⇒v^2 =u^2 −2gl(1+sin θ) mg sin θ=((mv^2 )/l) ⇒u^2 =gl(2+3 sin θ) ⇒v^2 =gl sin θ R=l cos θ h=l(1−sin θ)−b t=(R/(v cos ϕ))=(l/(v tan θ)) h=v sin ϕ (l/(v tan θ))−(1/2)g ((l/(v tan θ)))^2 l(1−sin θ)−b=((l cos θ)/(tan θ))−((gl^2 )/(2v^2 tan^2 θ)) ((gl^2 )/(2v^2 tan^2 θ))=b+l((1/(sin θ))−1) v^2 =((gl^2 )/(2 tan^2 θ [b+l(((1−sin θ)/(sin θ)))])) gl sin θ=((gl^2 )/(2 tan^2 θ [b+l(((1−sin θ)/(sin θ)))])) sin θ=(1/(2 tan^2 θ ((b/l)−1+(1/(sin θ))))) 2 sin^3 θ ((b/l)−1+(1/(sin θ)))=1−sin^2 θ ⇒2(1−(b/l))sin^3 θ−3 sin^2 θ+1=0 ⇒(1/(sin θ))=2 sin [(1/3) sin^(−1) (1−(b/l))+((2π)/3)] ⇒u=(√({2+(3/(2 sin [(1/3) sin^(−1) (1−(b/l))+((2π)/3)]))}gl))](Q109832.png)
Commented by ajfour last updated on 27/Aug/20
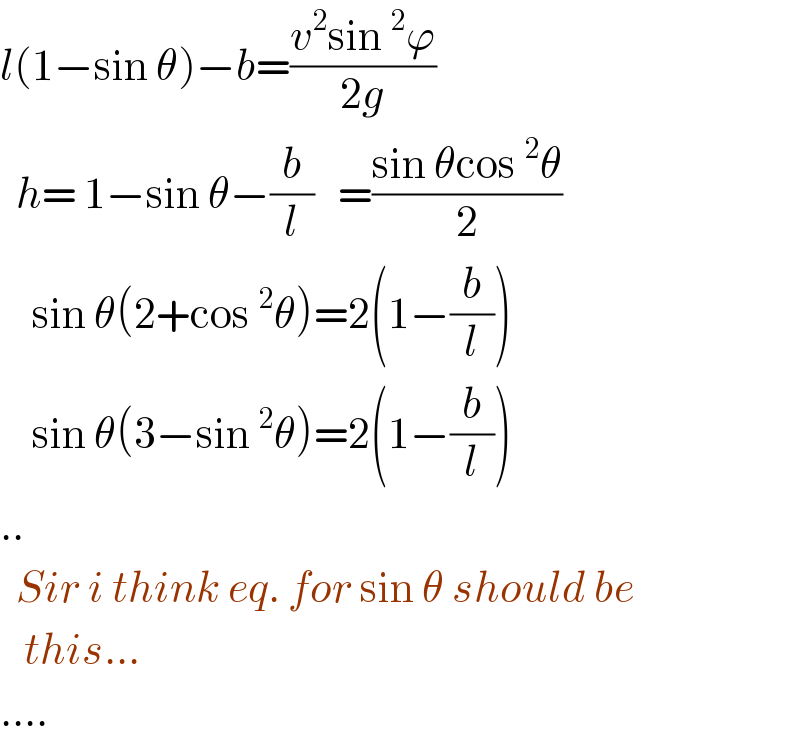
Commented by ajfour last updated on 27/Aug/20
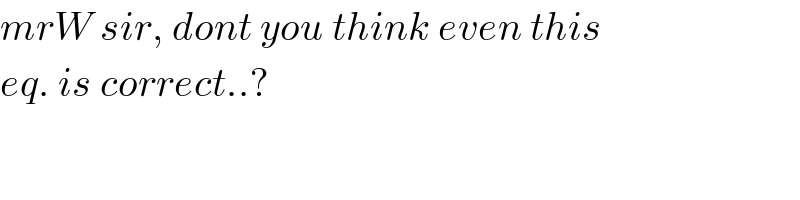
Commented by mr W last updated on 27/Aug/20

Commented by mr W last updated on 27/Aug/20
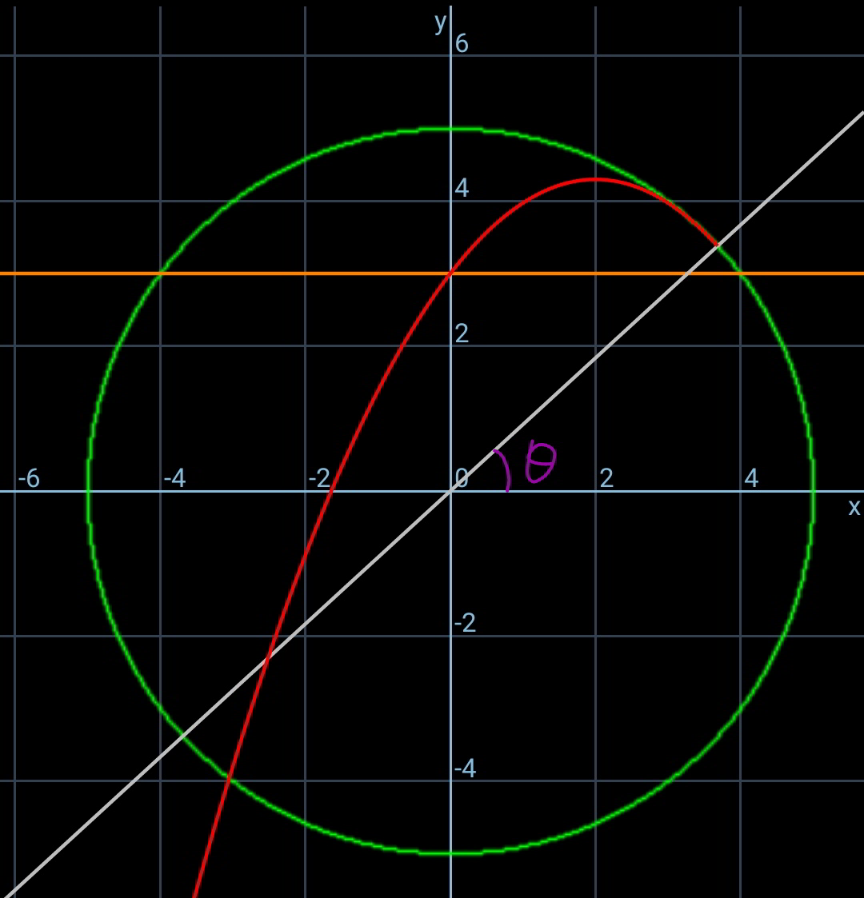
Commented by ajfour last updated on 27/Aug/20

Commented by mr W last updated on 27/Aug/20
![u=(√({2+(3/(2 sin [(1/3) sin^(−1) (1−(b/l))+((2π)/3)]))}gl))](Q110196.png)
Commented by mr W last updated on 29/Aug/20
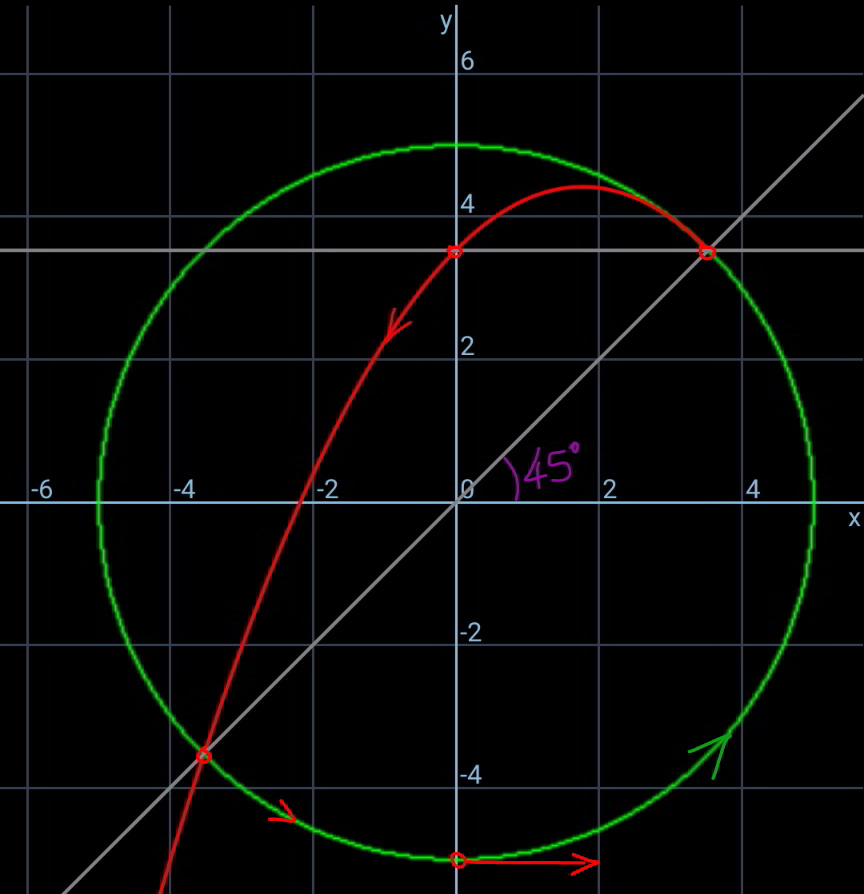
Commented by ajfour last updated on 29/Aug/20