
Question Number 109818 by Study last updated on 25/Aug/20

$${tanx}+{tan}\mathrm{2}{x}=\mathrm{1} \\ $$$${find}\:{the}\:{general}\:{solution} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Aug/20
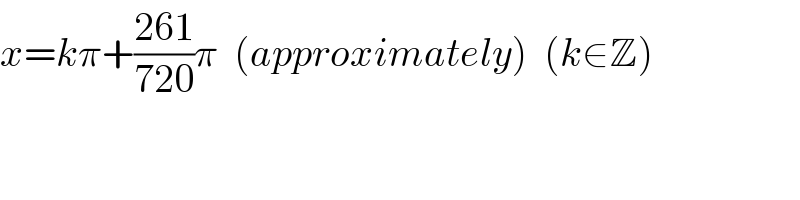
$${x}={k}\pi+\frac{\mathrm{261}}{\mathrm{720}}\pi\:\:\left({approximately}\right)\:\:\left({k}\in\mathbb{Z}\right) \\ $$
Commented by Study last updated on 25/Aug/20
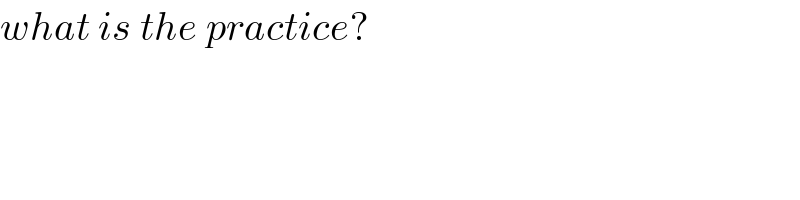
$${what}\:{is}\:{the}\:{practice}? \\ $$
Commented by Dwaipayan Shikari last updated on 25/Aug/20

$${tanx}+\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}=\mathrm{1} \\ $$$${t}+\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }=\mathrm{1} \\ $$$${t}−{t}^{\mathrm{3}} +\mathrm{2}{t}=\mathrm{1}−{t}^{\mathrm{2}} \\ $$$${t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=\mathrm{2}.\mathrm{17}.... \\ $$$${t}={another}\:{solution} \\ $$$${tanx}=\mathrm{2}.\mathrm{17}... \\ $$$${x}={k}\pi+\frac{\mathrm{261}}{\mathrm{720}}\pi\:\:\:\left({approx}\right) \\ $$
Commented by Study last updated on 25/Aug/20

$${help}\:{me} \\ $$
Commented by Study last updated on 25/Aug/20

$${i}\:{need}\:{your}\:{help} \\ $$
Commented by Study last updated on 25/Aug/20
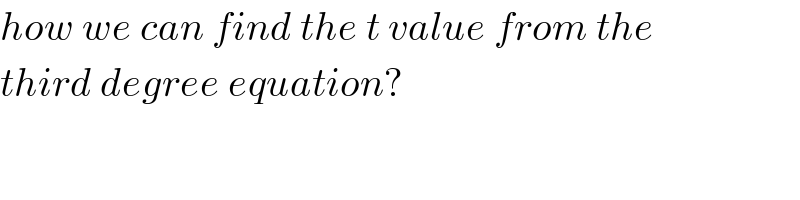
$${how}\:{we}\:{can}\:{find}\:{the}\:{t}\:{value}\:{from}\:{the} \\ $$$${third}\:{degree}\:{equation}? \\ $$
Commented by Her_Majesty last updated on 25/Aug/20

$${in}\:{this}\:{case}\:{you}\:{need}\:{the}\:{trigonometric} \\ $$$${solution}\:{method}.\:{search}\:{for}\:{it}\:{on}\:{the}\:{web} \\ $$$${anyway}\:{better}\:{use}\:{approximation} \\ $$$${we}\:{get} \\ $$$${t}_{\mathrm{1}} \approx−\mathrm{1}.\mathrm{48119} \\ $$$${t}_{\mathrm{2}} \approx.\mathrm{311108} \\ $$$${t}_{\mathrm{3}} \approx\mathrm{2}.\mathrm{17001} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =−.\mathrm{976957}+{n}\pi \\ $$$${x}_{\mathrm{2}} =.\mathrm{301616}+{n}\pi \\ $$$${x}_{\mathrm{3}} =\mathrm{1}.\mathrm{13899}+{n}\pi \\ $$
Answered by 1549442205PVT last updated on 26/Aug/20
![We need the condition x≠(π/2),x≠(π/4) tanx+((2tanx)/(1−tan^2 x))=1⇔tanx−tan^3 x+2tanx =1−tan^2 x⇔tan^3 x−tan^2 x−3tanx+1=0 ⇒cot^3 x−3cot^2 x−cotx+1=0 (cotx−1)^3 −4(cotx−1)−2=0 Put cotx−1=y we get y^3 −4y−2=0(2) Set y=(4/( (√3)))z.Replace into (2)we get ((64)/(3(√3)))z^3 −((16)/( (√3)))z−2=0.Multiplying two sides by ((3(√3))/(16)) we obtain: 4z^3 −3z−((3(√3))/8)=0(∗).On the other hands, we known that 4cos^3 u−3cosu−cos3u=0 Hence ,Put cos3u=((3(√3))/8)(3) then we see z=cosu is roots of the equation (∗) (3)⇔3u=cos^(−1) (((3(√3))/8))+2kπ⇔u=(1/3)[cos^(−1) (((3(√3))/8))+2kπ] Thus,the equation (∗)has three roots are z=cos(1/3)[cos^(−1) (((3(√3))/8))+2kπ](k=0,1,2) ⇒y=(4/( (√3)))z=(4/( (√3)))cos(1/3)[cos^(−1) (((3(√3))/8))+2kπ] ⇒cotx=y+1=1+(4/( (√3)))cos(1/3)[cos^(−1) (((3(√3))/8))+2kπ] ⇒tanx=(1/(1+(4/( (√3)))cos(1/3)[cos^(−1) (((3(√3))/8))+2kπ])) Thus,the given equation has roots are x=tan^(−1) {(1/(1+(4/( (√3)))cos(1/3)[cos^(−1) (((3(√3))/8))+2kπ]))}+mπ where k=0,1,2 and m∈Z](Q109971.png)
$$\mathrm{We}\:\mathrm{need}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{x}\neq\frac{\pi}{\mathrm{2}},\mathrm{x}\neq\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{tanx}+\frac{\mathrm{2tanx}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}=\mathrm{1}\Leftrightarrow\mathrm{tanx}−\mathrm{tan}^{\mathrm{3}} \mathrm{x}+\mathrm{2tanx} \\ $$$$=\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}\Leftrightarrow\mathrm{tan}^{\mathrm{3}} \mathrm{x}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{3tanx}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cot}^{\mathrm{3}} \mathrm{x}−\mathrm{3cot}^{\mathrm{2}} \mathrm{x}−\mathrm{cotx}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{cotx}−\mathrm{1}\right)^{\mathrm{3}} −\mathrm{4}\left(\mathrm{cotx}−\mathrm{1}\right)−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{Put}\:\mathrm{cotx}−\mathrm{1}=\mathrm{y}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{y}^{\mathrm{3}} −\mathrm{4y}−\mathrm{2}=\mathrm{0}\left(\mathrm{2}\right) \\ $$$$\mathrm{Set}\:\mathrm{y}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{z}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{64}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{z}^{\mathrm{3}} −\frac{\mathrm{16}}{\:\sqrt{\mathrm{3}}}\mathrm{z}−\mathrm{2}=\mathrm{0}.\mathrm{Multiplying}\:\mathrm{two} \\ $$$$\mathrm{sides}\:\mathrm{by}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{16}}\:\mathrm{we}\:\mathrm{obtain}: \\ $$$$\mathrm{4z}^{\mathrm{3}} −\mathrm{3z}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}=\mathrm{0}\left(\ast\right).\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands}, \\ $$$$\mathrm{we}\:\mathrm{known}\:\mathrm{that}\:\mathrm{4cos}^{\mathrm{3}} \mathrm{u}−\mathrm{3cosu}−\mathrm{cos3u}=\mathrm{0} \\ $$$$\mathrm{Hence}\:,\mathrm{Put}\:\mathrm{cos3u}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\left(\mathrm{3}\right)\:\mathrm{then}\:\mathrm{we}\:\mathrm{see} \\ $$$$\mathrm{z}=\mathrm{cosu}\:\mathrm{is}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\left(\ast\right) \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\mathrm{3u}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\Leftrightarrow\mathrm{u}=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\right] \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{equation}\:\left(\ast\right)\mathrm{has}\:\mathrm{three}\:\mathrm{roots} \\ $$$$\mathrm{are}\:\mathrm{z}=\mathrm{cos}\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\right]\left(\mathrm{k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{z}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\right] \\ $$$$\Rightarrow\mathrm{cotx}=\mathrm{y}+\mathrm{1}=\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\right] \\ $$$$\Rightarrow\mathrm{tanx}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\right]} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{roots}\:\mathrm{are} \\ $$$$\mathrm{x}=\mathrm{tan}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{cos}\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)+\mathrm{2k}\pi\right]}\right\}+\mathrm{m}\pi \\ $$$$\mathrm{where}\:\mathrm{k}=\mathrm{0},\mathrm{1},\mathrm{2}\:\mathrm{and}\:\mathrm{m}\in\mathbb{Z} \\ $$
