
Question and Answers Forum
Question Number 109838 by mnjuly1970 last updated on 25/Aug/20
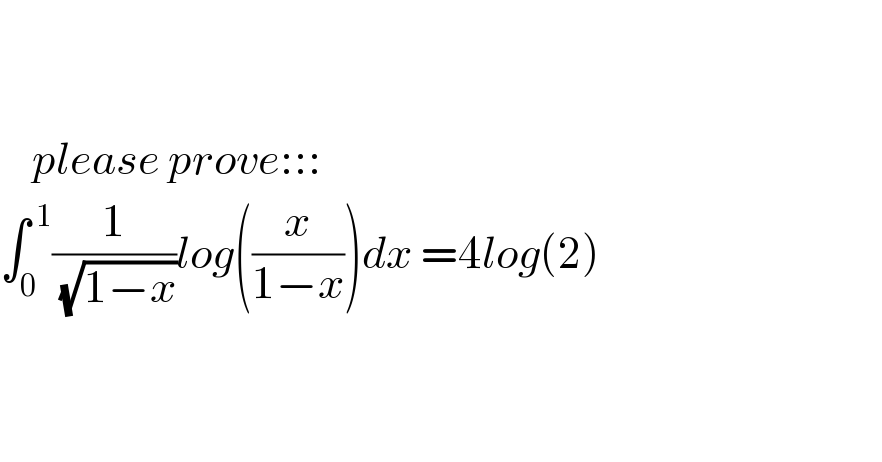
Answered by mathmax by abdo last updated on 25/Aug/20
![I =∫_0 ^1 (1/(√(1−x)))ln((x/(1−x)))dx changement (√(1−x))=t give 1−x =t^2 ⇒ I =−∫_0 ^1 (1/t)ln(((1−t^2 )/t^2 ))(−2t)dt =2 ∫_0 ^1 (ln(1−t^2 )−2ln(t))dt =2∫_0 ^1 ln(1−t^2 )dt −4∫_0 ^1 ln(t)dt we have ∫_0 ^1 ln(t)dt =[tlnt−t]_0 ^1 =−1 ∫_0 ^1 ln(1−t^2 )dt =_(by pafts) [(t−1) ln(1−t^2 )]_0 ^1 −∫_0 ^1 (t−1)×((−2t)/(1−t^2 ))dt =−2 ∫_0 ^1 ((t(1−t))/(1−t^2 ))dt =−2∫_0 ^1 (t/(1+t)) dt =−2∫_0 ^1 ((1+t−1)/(1+t)) dt =−2 +2ln(2) ⇒I =−4 +4ln(2)−4(−1) =4ln(2) ⇒ ★ ∫_0 ^1 (1/(√(1−x)))ln((x/(1−x)))dx =4ln(2)★](Q109840.png)
Commented by mnjuly1970 last updated on 26/Aug/20
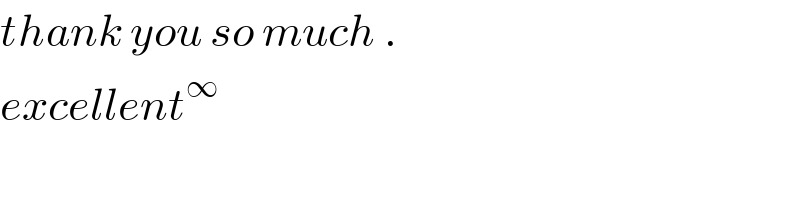
Commented by mathmax by abdo last updated on 27/Aug/20

