((★be★)/(math)) (1)∫ ((3+2cos x)/((2+3cos x)^3 )) dx (2)((√(2+(√3))) )^y −((√(2−(√3))) )^y = 14 y=?


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 109854 by bemath last updated on 26/Aug/20

$\frac{★ b e ★}{m a t h}$ $(1) \int \frac{3 + 2 \cos x}{{(2 + 3 \cos x)}^{3}} d x$ $(2) {(\sqrt{2 + \sqrt{3}})}^{y} - {(\sqrt{2 - \sqrt{3}})}^{y} = 14$ $y = ?$
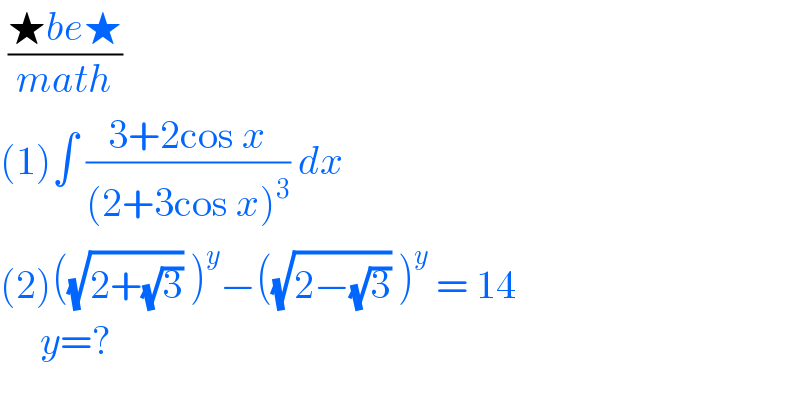
Commented by bemath last updated on 26/Aug/20

$t h a n k y o u b o t h$
	Answered by john santu last updated on 26/Aug/20

	$c o n s i d e r \sqrt{2 + \sqrt{3}} = \sqrt{(\frac{(2 + \sqrt{3}) (2 - \sqrt{3)}}{2 - \sqrt{3}})}$ $= \sqrt{\frac{1}{2 - \sqrt{3}}} = \frac{1}{\sqrt{2 - \sqrt{3}}}$ $s e t {(\sqrt{2 + \sqrt{3}})}^{y} = t$ $\Leftrightarrow t - \frac{1}{t} = 14 \Rightarrow t^{2} - 1 = 14 t$ $t^{2} - 14 t - 1 = 0, {(t - 7)}^{2} - 50 = 0$ $t = 7 + 5 \sqrt{2}; {(\sqrt{2 + \sqrt{3}})}^{y} = 7 + 5 \sqrt{2}$ ${(2 + \sqrt{3})}^{y} = {(7 + 5 \sqrt{2})}^{2}$ ${(2 + \sqrt{3})}^{y} = 99 + 70 \sqrt{2}$ $y = \frac{\ln (99 + 70 \sqrt{2})}{\ln (2 + \sqrt{3})} \approx 4.015497788$
	Answered by Her_Majesty last updated on 26/Aug/20

	$\sqrt{2 + \sqrt{3}} = \frac{\sqrt{6} + \sqrt{2}}{2}$ $\sqrt{2 - \sqrt{3}} = \frac{\sqrt{6} - \sqrt{2}}{2} = \frac{1}{\sqrt{2 + \sqrt{3}}}$ $a^{y} - \frac{1}{a^{y}} = 2 s i n h (y l n a) = 14 \Rightarrow y = \frac{{s i n h}^{- 1} 7}{l n a} =$ $= \frac{2 {s i n h}^{- 1} 7}{l n (2 + \sqrt{3})} = \frac{2 l n (7 + 5 \sqrt{2})}{l n (2 + \sqrt{3})}$
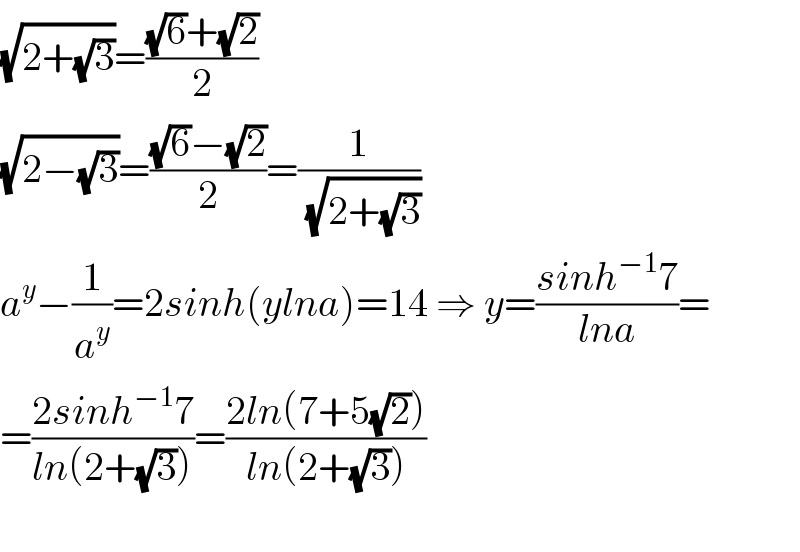
	Answered by Sarah85 last updated on 26/Aug/20

	$\int \frac{3 + 2 \cos x}{{(2 + 3 \cos x)}^{3}} d x$ $as usual : t = \tan \frac{x}{2}$ $- 2 \int \frac{(t^{2} + 1) (t^{2} + 5)}{{(t^{2} - 5)}^{3}} d t$ $I prefer {Ostrogradski}^{'} s Method I learned from$ $Sir MJS$ $\Rightarrow$ $\frac{t (7 t^{2} - 5)}{5 {(t^{2} - 5)}^{2}} - \frac{3}{5} \int \frac{d t}{t^{2} - 5} = \frac{t (7 t^{2} - 5)}{5 {(t^{2} - 5)}^{2}} - \frac{3 \sqrt{5}}{50} \ln \frac{\sqrt{5} t - 5}{\sqrt{5} t + 5} = . . .$
	Answered by 1549442205PVT last updated on 26/Aug/20
	$F=∫((3+2cosx)/((2+3cosx)^3 ))dx.Put t=tan(x/2) ⇒dt=(1/2)(1+t^2 )dx⇒dx=((2dt)/(1+t^2 )) 2+3cosx=2+3((1−t^2 )/(1+t^2 ))=((−t^2 +5)/(1+t^2 )) 3+2cosx=3+((2(1−t^2 ))/(1+t^2 ))=((t^2 +5)/(1+t^2 )) F=2∫(((t^2 +5)(t^2 +1)dt)/((−t^2 +5)^3 ))=−2∫(((t^2 +5)(t^2 +1)dt)/((t^2 −5)^3 )) Since (t^2 +5)(t^2 +1)=t^4 +6t^2 +5 =(t^2 −5)^2 +16(t^2 −5)+60 ,we have F=−∫[(2/(t^2 −5))+((32)/((t^2 −5)^2 ))+((60)/((t^2 −5)^3 ))]dt we have (1/(t^2 −5))=(1/((t+(√5))(t−(√5)))) =(1/(2(√5)))((1/(t−(√5)))−(1/(t+(√5)))). Put a= (1/(t−(√5))) b=(1/(t+(√5)))⇒ab=(1/(2(√5)))(a−b).Hence, (1/((t^2 −5)^2 ))=(ab)^2 =(1/(20))(a^2 +b^2 −(1/( (√5)))(a−b)) (1/((t^2 −5)^3 ))=(ab)^3 =(1/(40(√5)))(a^3 −b^3 −3ab(a−b)) =(1/(40(√5)))(a^3 −b^3 −(3/(2(√5)))(a−b)^2 ) =(1/(40(√5)))(a^3 −b^3 )−(3/(400))(a^2 +b^2 −(1/( (√5)))(a−b)) ∫a^3 dt=∫(dt/((t−(√5))^3 ))=((−1)/(2(t−(√5))^2 )),∫b^3 dt=((−1)/(2(t+(√5))^2 ))⇒∫(a^3 −b^3 )dt=(1/2)((1/((t+(√5))^2 ))−(1/((t−(√5))^2 )))=((−2t(√5))/((t^2 −5)^2 )) (1) ∫a^2 dt=∫(dt/((t−(√5))^2 ))=((−1)/(t−(√5))),∫b^2 dt=((−1)/(t+(√5)))⇒∫(a^2 +b^2 )dt=−((1/(t−(√5)))+(1/(t+(√5))))=((−2t)/(t^2 −5))(2) ∫(a−b)dt=∫((1/(t−(√5)))−(1/(t+(√5))))dt=ln∣((t−(√5))/(t+(√5)))∣(3) Consequemtly, 2ab+32(ab)^2 +120(ab)^3 =(1/( (√5)))(a−b)+((16)/(10))(a^2 +b^2 )−((16)/(10(√5)))(a−b)+(3/( (√5)))(a^3 −b^3 )−(9/(10))(a^2 +b^2 )+(9/(10(√5)))(a−b) =(3/( (√5)))(a^3 −b^3 )+(7/(10))(a^2 +b^2 )+(3/(10(√5)))(a−b) From (1)(2)(3)we get F=−{(3/( (√5)))×((2t(√5))/((t^2 −5)^2 ))+(7/(10))×((−2t)/(t^2 −5))+(3/(10(√5)))×ln∣((t−(√5))/(t+(√5)))∣} =((6t)/((t^2 −5)^2 ))+((7t)/(5(t^2 −5)))−(3/(10(√5)))ln∣((t−(√5))/(t+(√5)))∣=((t(7t^2 −5))/(5(t^2 −5)))−(3/(10(√5)))ln∣((t−(√5))/(t+(√5)))∣ =((tan(x/2)(7tan^2 (x/2)−5))/(5(tan^2 (x/2)−5)^2 ))−((3(√5))/(50))ln∣((tan(x/2)−(√5))/(tan(x/2)+(√5)))∣ 2)Since (√(2+(√3))) .(√(2−(√3)))=(√((2+(√3))(2−(√3)))) =(√(4−3))=1⇒((√(2+(√3))))^y .((√(2−(√3))))^y =1,so Put ((√(2+(√3))))^y =x(x>0)we get ((√(2−(√3))))^y =(1/x).Hence ((√(2+(√3))) )^y −((√(2−(√3))) )^y = 14 ⇔x−(1/x)=14⇔x^2 −14x−1=0 Δ′=7^2 +1=50=(5(√2))^2 ⇒x=7+5(√2) (root x=7−5(√2)<0⇒rejected).Hence ((√(2+(√3))))^y =7+5(√2) ⇒yln((√(2+(√3))))=ln(7+5(√2)) ⇔y=((ln(7+5(√2)))/(ln((√(2+(√3))))))≈4.0155$
	$F = \int \frac{3 + 2 cosx}{{(2 + 3 cosx)}^{3}} dx . Put t = \tan \frac{x}{2}$ $\Rightarrow dt = \frac{1}{2} (1 + t^{2}) dx \Rightarrow dx = \frac{2 dt}{1 + t^{2}}$ $2 + 3 cosx = 2 + 3 \frac{1 - t^{2}}{1 + t^{2}} = \frac{- t^{2} + 5}{1 + t^{2}}$ $3 + 2 cosx = 3 + \frac{2 (1 - t^{2})}{1 + t^{2}} = \frac{t^{2} + 5}{1 + t^{2}}$ $F = 2 \int \frac{(t^{2} + 5) (t^{2} + 1) dt}{{(- t^{2} + 5)}^{3}} = - 2 \int \frac{(t^{2} + 5) (t^{2} + 1) dt}{{(t^{2} - 5)}^{3}}$ $Since (t^{2} + 5) (t^{2} + 1) = t^{4} + {6 t}^{2} + 5$ $= {(t^{2} - 5)}^{2} + 16 (t^{2} - 5) + 60, we have$ $F = - \int [\frac{2}{t^{2} - 5} + \frac{32}{{(t^{2} - 5)}^{2}} + \frac{60}{{(t^{2} - 5)}^{3}}] dt$ $we have \frac{1}{t^{2} - 5} = \frac{1}{(t + \sqrt{5}) (t - \sqrt{5})}$ $= \frac{1}{2 \sqrt{5}} (\frac{1}{t - \sqrt{5}} - \frac{1}{t + \sqrt{5}}) . Put a = \frac{1}{t - \sqrt{5}}$ $b = \frac{1}{t + \sqrt{5}} \Rightarrow ab = \frac{1}{2 \sqrt{5}} (a - b) . Hence,$ $\frac{1}{{(t^{2} - 5)}^{2}} = {(ab)}^{2} = \frac{1}{20} (a^{2} + b^{2} - \frac{1}{\sqrt{5}} (a - b))$ $\frac{1}{{(t^{2} - 5)}^{3}} = {(ab)}^{3} = \frac{1}{40 \sqrt{5}} (a^{3} - b^{3} - 3 ab (a - b))$ $= \frac{1}{40 \sqrt{5}} (a^{3} - b^{3} - \frac{3}{2 \sqrt{5}} {(a - b)}^{2})$ $= \frac{1}{40 \sqrt{5}} (a^{3} - b^{3}) - \frac{3}{400} (a^{2} + b^{2} - \frac{1}{\sqrt{5}} (a - b))$ $\int a^{3} dt = \int \frac{dt}{{(t - \sqrt{5})}^{3}} = \frac{- 1}{2 {(t - \sqrt{5})}^{2}}, \int b^{3} dt = \frac{- 1}{2 {(t + \sqrt{5})}^{2}} \Rightarrow \int (a^{3} - b^{3}) dt = \frac{1}{2} (\frac{1}{{(t + \sqrt{5})}^{2}} - \frac{1}{{(t - \sqrt{5})}^{2}}) = \frac{- 2 t \sqrt{5}}{{(t^{2} - 5)}^{2}} (1)$ $\int a^{2} dt = \int \frac{dt}{{(t - \sqrt{5})}^{2}} = \frac{- 1}{t - \sqrt{5}}, \int b^{2} dt = \frac{- 1}{t + \sqrt{5}} \Rightarrow \int (a^{2} + b^{2}) dt = - (\frac{1}{t - \sqrt{5}} + \frac{1}{t + \sqrt{5}}) = \frac{- 2 t}{t^{2} - 5} (2)$ $\int (a - b) dt = \int (\frac{1}{t - \sqrt{5}} - \frac{1}{t + \sqrt{5}}) dt = \ln ∣ \frac{t - \sqrt{5}}{t + \sqrt{5}} ∣ (3)$ $Consequemtly,$ $2 ab + 32 {(ab)}^{2} + 120 {(ab)}^{3} = \frac{1}{\sqrt{5}} (a - b) + \frac{16}{10} (a^{2} + b^{2}) - \frac{16}{10 \sqrt{5}} (a - b) + \frac{3}{\sqrt{5}} (a^{3} - b^{3}) - \frac{9}{10} (a^{2} + b^{2}) + \frac{9}{10 \sqrt{5}} (a - b)$ $= \frac{3}{\sqrt{5}} (a^{3} - b^{3}) + \frac{7}{10} (a^{2} + b^{2}) + \frac{3}{10 \sqrt{5}} (a - b)$ $From (1) (2) (3) we get$ $F = - {\frac{3}{\sqrt{5}} \times \frac{2 t \sqrt{5}}{{(t^{2} - 5)}^{2}} + \frac{7}{10} \times \frac{- 2 t}{t^{2} - 5} + \frac{3}{10 \sqrt{5}} \times \ln ∣ \frac{t - \sqrt{5}}{t + \sqrt{5}} ∣}$ $= \frac{6 t}{{(t^{2} - 5)}^{2}} + \frac{7 t}{5 (t^{2} - 5)} - \frac{3}{10 \sqrt{5}} \ln ∣ \frac{t - \sqrt{5}}{t + \sqrt{5}} ∣= \frac{t ({7 t}^{2} - 5)}{5 (t^{2} - 5)} - \frac{3}{10 \sqrt{5}} \ln ∣ \frac{t - \sqrt{5}}{t + \sqrt{5}} ∣$ $= \frac{\tan \frac{x}{2} (7 \tan^{2} \frac{x}{2} - 5)}{5 {(\tan^{2} \frac{x}{2} - 5)}^{2}} - \frac{3 \sqrt{5}}{50} \ln ∣ \frac{\tan \frac{x}{2} - \sqrt{5}}{\tan \frac{x}{2} + \sqrt{5}} ∣$ $2) Since \sqrt{2 + \sqrt{3}} . \sqrt{2 - \sqrt{3}} = \sqrt{(2 + \sqrt{3}) (2 - \sqrt{3}})$ $= \sqrt{4 - 3} = 1 \Rightarrow {(\sqrt{2 + \sqrt{3}})}^{y} . {(\sqrt{2 - \sqrt{3}})}^{y} = 1, so$ $Put {(\sqrt{2 + \sqrt{3}})}^{y} = x (x > 0) we get$ ${(\sqrt{2 - \sqrt{3}})}^{y} = \frac{1}{x} . Hence$ ${(\sqrt{2 + \sqrt{3}})}^{y} - {(\sqrt{2 - \sqrt{3}})}^{y} = 14$ $\Leftrightarrow x - \frac{1}{x} = 14 \Leftrightarrow x^{2} - 14 x - 1 = 0$ $Δ^{'} = 7^{2} + 1 = 50 = {(5 \sqrt{2})}^{2} \Rightarrow x = 7 + 5 \sqrt{2}$ $(root x = 7 - 5 \sqrt{2} < 0 \Rightarrow rejected) . Hence$ ${(\sqrt{2 + \sqrt{3}})}^{y} = 7 + 5 \sqrt{2} \Rightarrow yln (\sqrt{2 + \sqrt{3}}) = \ln (7 + 5 \sqrt{2})$ $\Leftrightarrow y = \frac{\ln (7 + 5 \sqrt{2})}{\ln (\sqrt{2 + \sqrt{3}})} \approx 4.0155$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum