Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 109855 by aurpeyz last updated on 26/Aug/20

Answered by aurpeyz last updated on 26/Aug/20

$$Cananyoneplsexplainthis?itispertaining$$$$binomialexpansionfornegativepowers$$

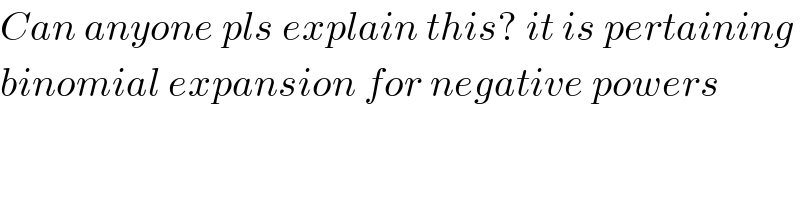
Commented by mathdave last updated on 26/Aug/20

$$eitherforpositiveornegativedegreepower$$$$alwaysusethisgeneralizationformular$$$${(x+y)}^n=\frac{x^n}{0!}+\frac{{nx}^{n-1}y}{1!}+\frac{n(n-1)x^{n-2}{y}^2}{2!}+\frac{n(n-1)(n-2)x^{n-3}{y}^3}{3!}..........$$

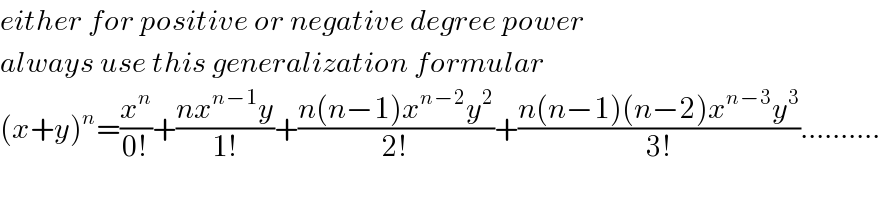
Answered by Her_Majesty last updated on 26/Aug/20

$$\underset{j=0}{\sum ^n}{x}^j=\frac{x^{n+1}-1}{x-1}$$$${lim}_{n\to \mathrm{\infty }}\frac{x^{n+1}-1}{x-1}onlyexistsif\mid x\mid <1$$$$inthiscase{x}^{n+1}=0\Rightarrow \underset{j=0}{\sum ^{\mathrm{\infty }}}{x}^j=\frac{1}{1-x}with\mid x\mid <1$$

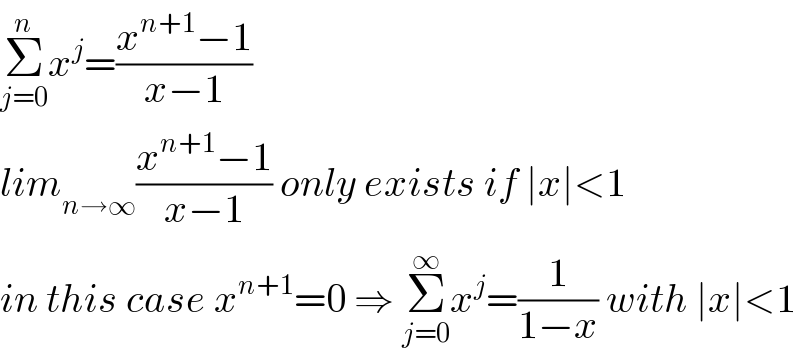
Answered by Rio Michael last updated on 26/Aug/20

$$\mathrm{Given}\mathrm{the}\mathrm{general}\mathrm{binomial}\mathrm{expansion}{(1+x)}^n,\mathrm{then}\mathrm{general}$$$$\mathrm{term}\mathrm{expressed}\mathrm{as}\mathrm{a}\mathrm{summation}\mathrm{is}\mathrm{given}\mathrm{as}$$$${(1+x)}^n=\underset{k=0}{\sum ^n}{}^n{C}_k{x}^{n-k}$$$$\mathrm{It}\mathrm{is}\mathrm{known}\mathrm{that}\mathrm{the}\mathrm{series}\mathrm{is}\mathrm{convergent}\mathrm{if}\mid x\mid <1.$$$$\mathrm{If}\mathrm{we}\mathrm{wish}\mathrm{to}\mathrm{expand}\mathrm{such}\mathrm{that}\mid x\mid >1,\mathrm{then}\mathrm{it}$$$$\mathrm{must}\mathrm{be}\mathrm{expanded}\mathrm{in}\mathrm{terms}\mathrm{of}\frac{1}{x},\mathrm{this}\mathrm{works}\mathrm{since}\frac{1}{x}<1$$$$\mathrm{and}\mathrm{will}\mathrm{be}\mathrm{carried}\mathrm{out}\mathrm{for}\mathrm{the}{\mathrm{expansion}}^{\prime }\mathrm{s}\mathrm{of}{(1+x)}^{-n}\mathrm{only}.$$

Commented by aurpeyz last updated on 26/Aug/20

$$pls.\mathrm{What}\mathrm{is}\mathrm{the}\mathrm{implication}\mathrm{of}\mathrm{this}\mathrm{statement}?$$$$\mathrm{Does}\mathrm{that}\mathrm{mean}\mathrm{that}\mathrm{i}\mathrm{have}\mathrm{to}\mathrm{factorize}$$$$\mathrm{any}\mathrm{question}\mathrm{on}\mathrm{negative}\mathrm{power}\mathrm{binomial}\mathrm{to}$$$$\mathrm{get}\mathrm{the}\mathrm{form}\frac{1}{\mathrm{x}}\mathrm{in}\mathrm{other}\mathrm{to}\mathrm{get}\mathrm{the}\mathrm{right}\mathrm{ans}$$

Commented by aurpeyz last updated on 26/Aug/20

$$\mathrm{That}\mathrm{is}\mathrm{exactly}\mathrm{where}\mathrm{I}\mathrm{am}\mathrm{getting}\mathrm{confused}.$$$$\mathrm{Anytime}\mathrm{i}\mathrm{have}\mathrm{a}\mathrm{negative}\mathrm{power}.\mathrm{I}\mathrm{always}$$$$\mathrm{factorize}\mathrm{the}\mathrm{binomial}\mathrm{to}\mathrm{get}\mathrm{the}\mathrm{form}\frac{1}{\mathrm{x}}\mathrm{in}$$$$\mathrm{expansion}.\mathrm{but}\mathrm{the}\mathrm{problem}\mathrm{is}\mathrm{that}\mathrm{it}\mathrm{doesnt}\mathrm{work}$$$$\mathrm{for}\mathrm{all}\mathrm{kinds}\mathrm{of}\mathrm{problem}$$

Commented by Rio Michael last updated on 26/Aug/20

$$\mathrm{No}\mathrm{its}\mathrm{expansion}\mathrm{as}\mathrm{you}\mathrm{would}\mathrm{for}\mathrm{anyother}\mathrm{problem}.$$$$\mathrm{Most}\mathrm{at}\mathrm{times}\mathrm{it}\mathrm{will}\mathrm{appear}\mathrm{in}\mathrm{terms}\mathrm{of}\frac{1}{x},\mathrm{if}\mathrm{it}{\mathrm{doesn}}^{\prime }\mathrm{t}$$$$\mathrm{then}\mathrm{either}\mathrm{the}\mathrm{series}{\mathrm{doesn}}^{\prime }\mathrm{t}\mathrm{converge}\mathrm{or}{\mathrm{it}}^{\prime }\mathrm{s}\mathrm{got}\mathrm{a}\mathrm{particular}$$$$\mathrm{range}\mathrm{of}\mathrm{numbers}\mathrm{for}\mathrm{which}\mathrm{it}\mathrm{converges}.$$

Commented by aurpeyz last updated on 27/Aug/20

$$Sir.PlscheckquestionQ.110109helpmewiththeexpansion$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com