Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 110015 by ZiYangLee last updated on 26/Aug/20

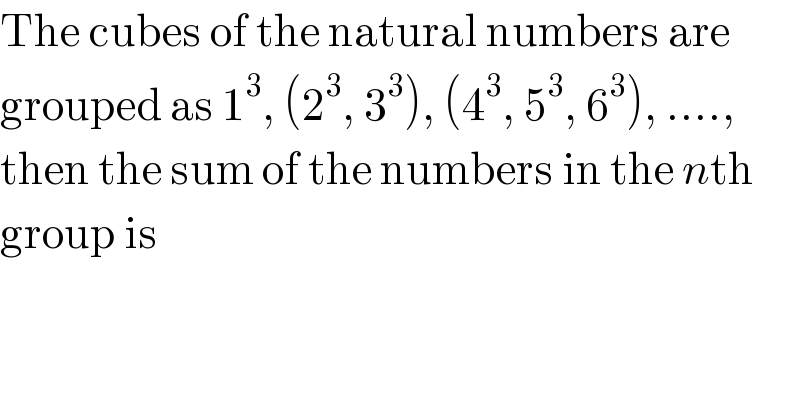
The cubes of the natural numbers are grouped as 1^3 , (2^3 , 3^3 ), (4^3 , 5^3 , 6^3 ), ...., then the sum of the numbers in the nth group is

$$\mathrm{The}\:\mathrm{cubes}\:\mathrm{of}\:\mathrm{the}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{are} \\ $$$$\mathrm{grouped}\:\mathrm{as}\:\mathrm{1}^{\mathrm{3}} ,\:\left(\mathrm{2}^{\mathrm{3}} ,\:\mathrm{3}^{\mathrm{3}} \right),\:\left(\mathrm{4}^{\mathrm{3}} ,\:\mathrm{5}^{\mathrm{3}} ,\:\mathrm{6}^{\mathrm{3}} \right),\:...., \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{in}\:\mathrm{the}\:{n}\mathrm{th} \\ $$$$\mathrm{group}\:\mathrm{is} \\ $$

Commented by Dwaipayan Shikari last updated on 26/Aug/20

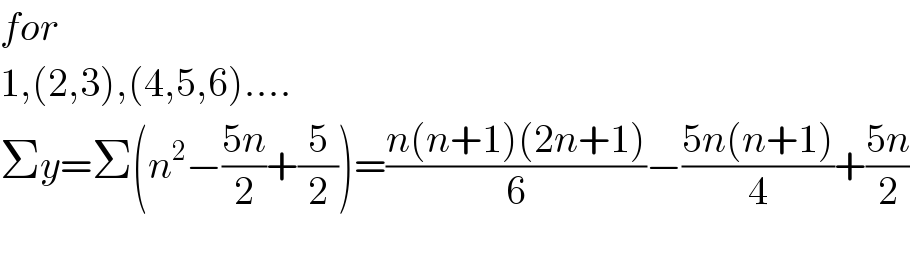
for 1,(2,3),(4,5,6).... Σy=Σ(n^2 −((5n)/2)+(5/2))=((n(n+1)(2n+1))/6)−((5n(n+1))/4)+((5n)/2)

$${for} \\ $$$$\mathrm{1},\left(\mathrm{2},\mathrm{3}\right),\left(\mathrm{4},\mathrm{5},\mathrm{6}\right).... \\ $$$$\Sigma{y}=\Sigma\left({n}^{\mathrm{2}} −\frac{\mathrm{5}{n}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}}\right)=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}−\frac{\mathrm{5}{n}\left({n}+\mathrm{1}\right)}{\mathrm{4}}+\frac{\mathrm{5}{n}}{\mathrm{2}} \\ $$$$ \\ $$

Answered by Dwaipayan Shikari last updated on 26/Aug/20

nth group first term is y^3 y △y△^2 y 1 1 2 1 2 4 1 3 7 y=1+(n−1)+(1/2)(n−1)(n−2)=(n^2 −((5n)/2)+(5/2)) y^3 =(n^2 −((5n)/2)+(5/2))^3 Σ_(n=1) ^n (n^2 −((5n)/2)+(5/2))^3 =(1/(672))n(96n^6 −504n^5 +1344n^4 −2205n^3 +2618n^2 −2205n+1528)

$${nth}\:{group}\:{first}\:{term}\:{is}\:{y}^{\mathrm{3}} \\ $$$${y}\:\bigtriangleup{y}\bigtriangleup^{\mathrm{2}} {y} \\ $$$$\mathrm{1} \\ $$$$\:\:\:\:\:\:\mathrm{1} \\ $$$$\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\mathrm{2} \\ $$$$\mathrm{4}\:\:\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{3} \\ $$$$\mathrm{7} \\ $$$${y}=\mathrm{1}+\left({n}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)=\left({n}^{\mathrm{2}} −\frac{\mathrm{5}{n}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$${y}^{\mathrm{3}} =\left({n}^{\mathrm{2}} −\frac{\mathrm{5}{n}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left({n}^{\mathrm{2}} −\frac{\mathrm{5}{n}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{672}}{n}\left(\mathrm{96}{n}^{\mathrm{6}} −\mathrm{504}{n}^{\mathrm{5}} +\mathrm{1344}{n}^{\mathrm{4}} −\mathrm{2205}{n}^{\mathrm{3}} +\mathrm{2618}{n}^{\mathrm{2}} −\mathrm{2205}{n}+\mathrm{1528}\right) \\ $$

Commented by aurpeyz last updated on 26/Aug/20

Pls explain how you got the numbers you wrote in the first 9 lines and hou you arrived at n^2 −((5n)/2)+(5/2)

$${Pls}\:{explain}\:{how}\:{you}\:{got}\:{the}\:{numbers}\:{you}\:{wrote}\: \\ $$$${in}\:{the}\:{first}\:\mathrm{9}\:{lines}\:{and}\:{hou}\:{you}\:{arrived}\:{at}\: \\ $$$${n}^{\mathrm{2}} −\frac{\mathrm{5}{n}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{2}} \\ $$

Commented by Dwaipayan Shikari last updated on 26/Aug/20

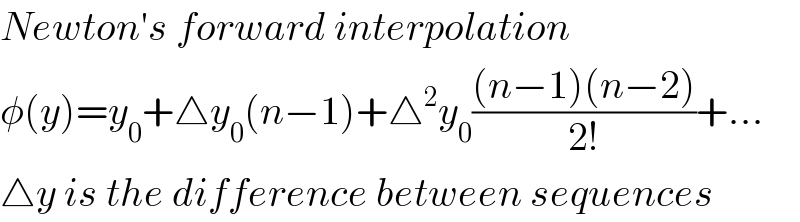
Newton′s forward interpolation φ(y)=y_0 +△y_0 (n−1)+△^2 y_0 (((n−1)(n−2))/(2!))+... △y is the difference between sequences

$${Newton}'{s}\:{forward}\:{interpolation} \\ $$$$\phi\left({y}\right)={y}_{\mathrm{0}} +\bigtriangleup{y}_{\mathrm{0}} \left({n}−\mathrm{1}\right)+\bigtriangleup^{\mathrm{2}} {y}_{\mathrm{0}} \frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}!}+... \\ $$$$\bigtriangleup{y}\:{is}\:{the}\:{difference}\:{between}\:{sequences} \\ $$

Commented by Dwaipayan Shikari last updated on 26/Aug/20

https://en.m.wikipedia.org/wiki/Interpolation

Commented by aurpeyz last updated on 27/Aug/20

I understand. how come you use 1 2 4 7?

$$\mathrm{I}\:\mathrm{understand}.\:\mathrm{how}\:\mathrm{come}\:\mathrm{you}\:\mathrm{use}\:\mathrm{1}\:\mathrm{2}\:\mathrm{4}\:\mathrm{7}? \\ $$

Answered by mr W last updated on 27/Aug/20

1+2+3+...+(n−1)=(((n−1)n)/2) the sum of the nth group is: S_n =Σ_(k=(((n−1)n)/2)+1) ^((((n−1)n)/2)+n) k^3 =Σ_(k=1) ^((((n−1)n)/2)+n) k^3 −Σ_(k=1) ^(((n−1)n)/2) k^3 =[(1/2)((((n−1)n)/2)+n)((((n−1)n)/2)+n+1)]^2 −[(1/2)((((n−1)n)/2))((((n−1)n)/2)+1)]^2 =((n^2 [(n+1)^2 (n^2 +n+2)^2 −(n−1)^2 (n^2 −n+2)^2 )/(64))] =((n^3 (n^2 +1)(n^2 +3))/8)

$$\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\left({n}−\mathrm{1}\right)=\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}} \\ $$$${the}\:{sum}\:{of}\:{the}\:{nth}\:{group}\:{is}: \\ $$$${S}_{{n}} =\underset{{k}=\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+\mathrm{1}} {\overset{\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+{n}} {\sum}}{k}^{\mathrm{3}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+{n}} {\sum}}{k}^{\mathrm{3}} −\underset{{k}=\mathrm{1}} {\overset{\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}} {\sum}}{k}^{\mathrm{3}} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+{n}\right)\left(\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+{n}+\mathrm{1}\right)\right]^{\mathrm{2}} \\ $$$$−\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}\right)\left(\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+\mathrm{1}\right)\right]^{\mathrm{2}} \\ $$$$\left.=\frac{{n}^{\mathrm{2}} \left[\left({n}+\mathrm{1}\right)^{\mathrm{2}} \left({n}^{\mathrm{2}} +{n}+\mathrm{2}\right)^{\mathrm{2}} −\left({n}−\mathrm{1}\right)^{\mathrm{2}} \left({n}^{\mathrm{2}} −{n}+\mathrm{2}\right)^{\mathrm{2}} \right.}{\mathrm{64}}\right] \\ $$$$=\frac{{n}^{\mathrm{3}} \left({n}^{\mathrm{2}} +\mathrm{1}\right)\left({n}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{8}} \\ $$

Commented by mr W last updated on 26/Aug/20

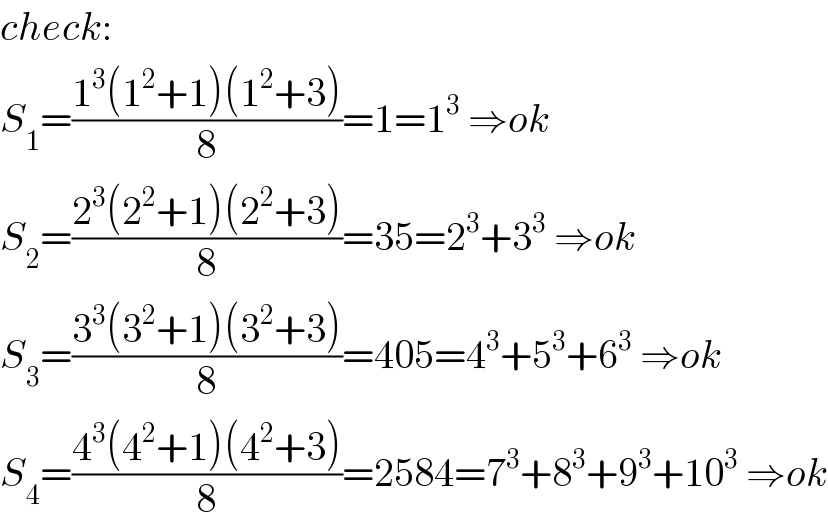
check: S_1 =((1^3 (1^2 +1)(1^2 +3))/8)=1=1^3 ⇒ok S_2 =((2^3 (2^2 +1)(2^2 +3))/8)=35=2^3 +3^3 ⇒ok S_3 =((3^3 (3^2 +1)(3^2 +3))/8)=405=4^3 +5^3 +6^3 ⇒ok S_4 =((4^3 (4^2 +1)(4^2 +3))/8)=2584=7^3 +8^3 +9^3 +10^3 ⇒ok

$${check}: \\ $$$${S}_{\mathrm{1}} =\frac{\mathrm{1}^{\mathrm{3}} \left(\mathrm{1}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{8}}=\mathrm{1}=\mathrm{1}^{\mathrm{3}} \:\Rightarrow{ok} \\ $$$${S}_{\mathrm{2}} =\frac{\mathrm{2}^{\mathrm{3}} \left(\mathrm{2}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{8}}=\mathrm{35}=\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} \:\Rightarrow{ok} \\ $$$${S}_{\mathrm{3}} =\frac{\mathrm{3}^{\mathrm{3}} \left(\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{8}}=\mathrm{405}=\mathrm{4}^{\mathrm{3}} +\mathrm{5}^{\mathrm{3}} +\mathrm{6}^{\mathrm{3}} \:\Rightarrow{ok} \\ $$$${S}_{\mathrm{4}} =\frac{\mathrm{4}^{\mathrm{3}} \left(\mathrm{4}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{8}}=\mathrm{2584}=\mathrm{7}^{\mathrm{3}} +\mathrm{8}^{\mathrm{3}} +\mathrm{9}^{\mathrm{3}} +\mathrm{10}^{\mathrm{3}} \:\Rightarrow{ok} \\ $$

Commented by ZiYangLee last updated on 27/Aug/20

Love your solution the most ==

$$\mathrm{Love}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{the}\:\mathrm{most}\:== \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com