Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 110109 by aurpeyz last updated on 27/Aug/20

Answered by $@y@m last updated on 27/Aug/20

Commented by Rio Michael last updated on 27/Aug/20

(3x)^(−2) (1 + (1/(3x)))^(−2) = (1/(9x^2 ))( 1 −(2/(3x)) + (1/(3x^2 ))−(4/(27x^3 )) + ...) (your textbook approach) (3x)^(−2) (1 + (1/(3x)))^(−2) = (3x)^(−2) [1+ (−2)((1/(3x))) + ((−2(−3))/(2!))((1/(3x)))^2 + ((−2(−3)(−4))/(3!))((1/(3x)))^3 +...] = (3x)^(−2) [1−(2/(3x)) + (1/(3x^2 )) − (4/(27x^3 )) +...] valid for ∣(1/(3x))∣ < 1 ⇒ ∣3x∣ <1 ⇔ −(1/3) < x < (1/3) same answer, basically thesame answers.No big difference.

$$\left(\mathrm{3}{x}\right)^{−\mathrm{2}} \left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{−\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{9}{x}^{\mathrm{2}} }\left(\:\mathrm{1}\:−\frac{\mathrm{2}}{\mathrm{3}{x}}\:+\:\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{27}{x}^{\mathrm{3}} }\:+\:...\right)\: \\ $$$$\left(\mathrm{your}\:\mathrm{textbook}\:\mathrm{approach}\right) \\ $$$$\left(\mathrm{3}{x}\right)^{−\mathrm{2}} \left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{−\mathrm{2}} \:=\:\left(\mathrm{3}{x}\right)^{−\mathrm{2}} \left[\mathrm{1}+\:\left(−\mathrm{2}\right)\left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)\:+\:\frac{−\mathrm{2}\left(−\mathrm{3}\right)}{\mathrm{2}!}\left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{\mathrm{2}} \:+\:\frac{−\mathrm{2}\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)}{\mathrm{3}!}\left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{\mathrm{3}} +...\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{3}{x}\right)^{−\mathrm{2}} \left[\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}{x}}\:+\:\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{4}}{\mathrm{27}{x}^{\mathrm{3}} }\:+...\right] \\ $$$$\mathrm{valid}\:\mathrm{for}\:\mid\frac{\mathrm{1}}{\mathrm{3}{x}}\mid\:<\:\mathrm{1}\:\:\Rightarrow\:\:\mid\mathrm{3}{x}\mid\:<\mathrm{1}\:\Leftrightarrow\:−\frac{\mathrm{1}}{\mathrm{3}}\:<\:{x}\:<\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{same}\:\mathrm{answer},\:\mathrm{basically}\:\mathrm{thesame}\:\mathrm{answers}.\mathrm{No}\: \\ $$$$\mathrm{big}\:\mathrm{difference}. \\ $$

Commented by aurpeyz last updated on 27/Aug/20

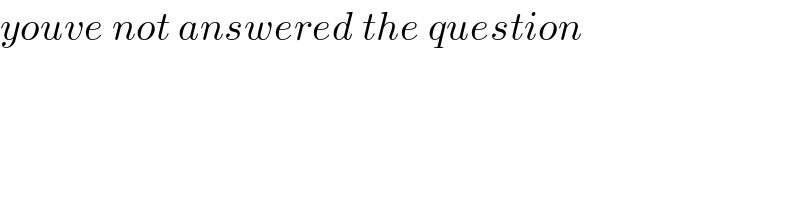
youve not answered the question

$${youve}\:{not}\:{answered}\:{the}\:{question} \\ $$

Commented by aurpeyz last updated on 27/Aug/20

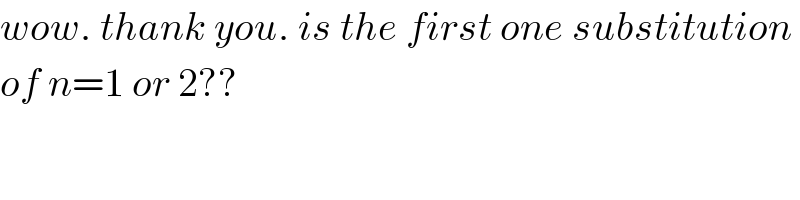
wow. thank you. is the first one substitution of n=1 or 2??

$${wow}.\:{thank}\:{you}.\:{is}\:{the}\:{first}\:{one}\:{substitution} \\ $$$${of}\:{n}=\mathrm{1}\:{or}\:\mathrm{2}?? \\ $$

Commented by $@y@m last updated on 27/Aug/20

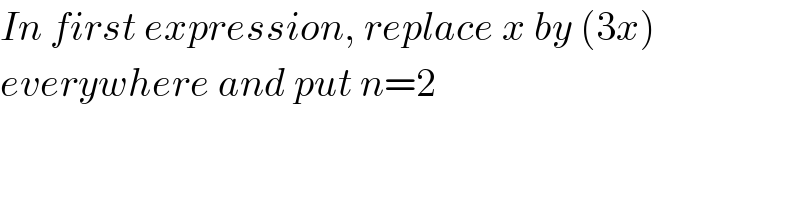
In first expression, replace x by (3x) everywhere and put n=2

$${In}\:{first}\:{expression},\:{replace}\:{x}\:{by}\:\left(\mathrm{3}{x}\right) \\ $$$${everywhere}\:{and}\:{put}\:{n}=\mathrm{2} \\ $$

Commented by aurpeyz last updated on 27/Aug/20

my textbook factorized 3x to get (3x)^(−2) [1+(1/(3x))]^(−2) =(1/((3x)^2 ))[1−(2/(3x))+(1/(3x^2 ))−(4/(27x^3 ))...] and i want to see if anyone can pls expslain why it is like that and when i am to use that approach.

$${my}\:{textbook}\:{factorized}\:\mathrm{3}{x}\:{to}\:{get} \\ $$$$\left(\mathrm{3}{x}\right)^{−\mathrm{2}} \left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}{x}}\right]^{−\mathrm{2}} =\frac{\mathrm{1}}{\left(\mathrm{3}{x}\right)^{\mathrm{2}} }\left[\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}{x}}+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{27}{x}^{\mathrm{3}} }...\right] \\ $$$${and}\:{i}\:{want}\:{to}\:{see}\:{if}\:{anyone}\:{can}\:{pls}\:{expslain} \\ $$$${why}\:{it}\:{is}\:{like}\:{that}\:{and}\:{when}\:{i}\:{am}\:{to}\:{use}\:{that} \\ $$$${approach}. \\ $$

Commented by $@y@m last updated on 27/Aug/20

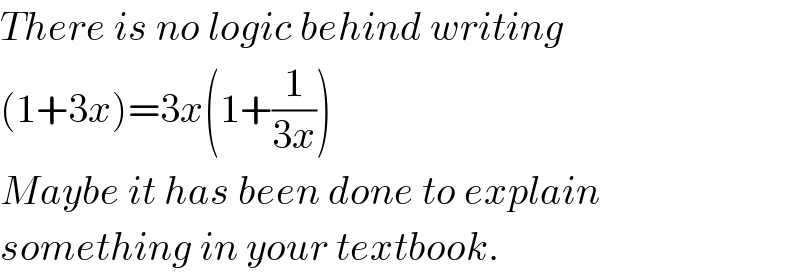
There is no logic behind writing (1+3x)=3x(1+(1/(3x))) Maybe it has been done to explain something in your textbook.

$${There}\:{is}\:{no}\:{logic}\:{behind}\:{writing} \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}\right)=\mathrm{3}{x}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}{x}}\right) \\ $$$${Maybe}\:{it}\:{has}\:{been}\:{done}\:{to}\:{explain} \\ $$$${something}\:{in}\:{your}\:{textbook}. \\ $$

Answered by Rio Michael last updated on 27/Aug/20

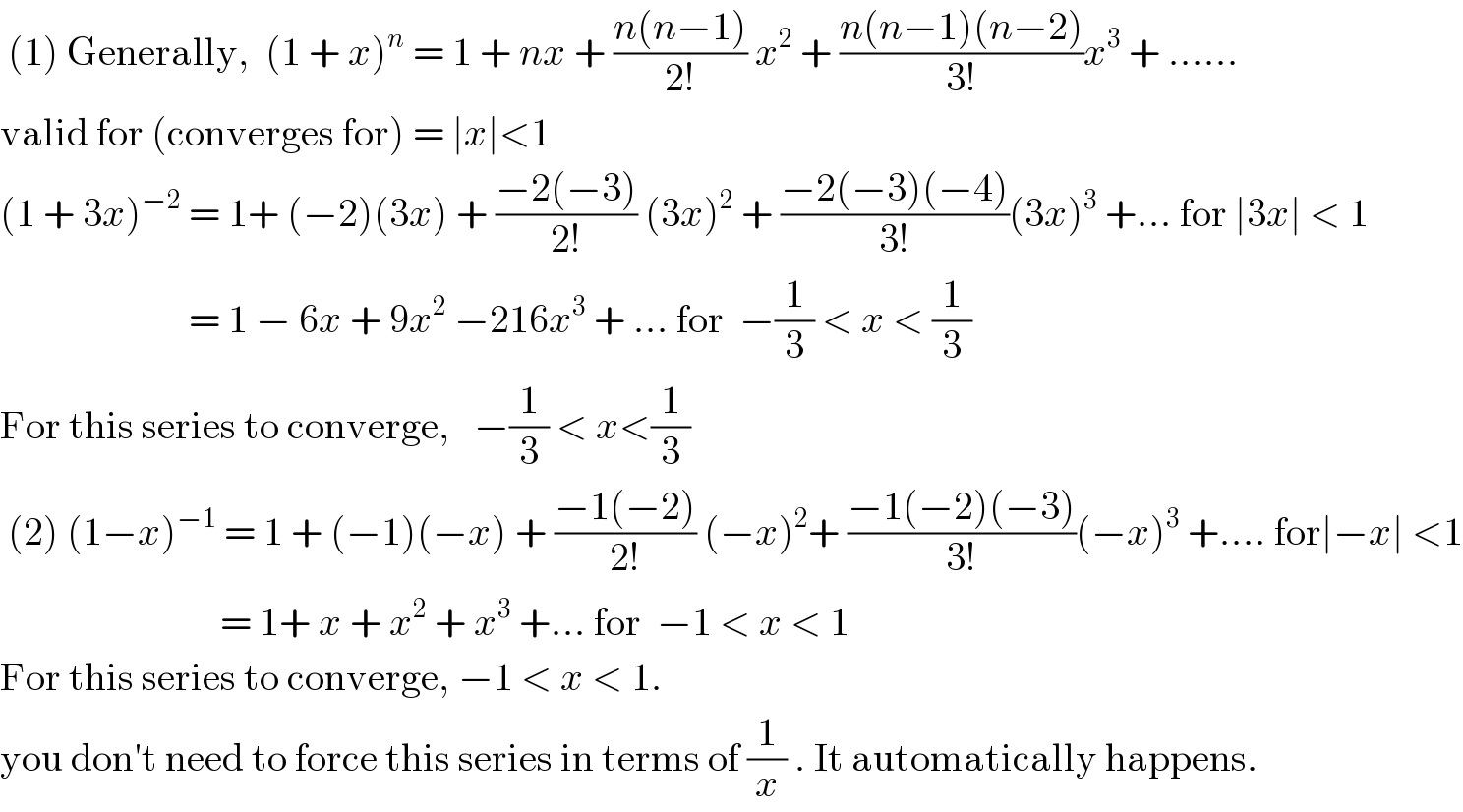
(1) Generally, (1 + x)^n = 1 + nx + ((n(n−1))/(2!)) x^2 + ((n(n−1)(n−2))/(3!))x^3 + ...... valid for (converges for) = ∣x∣<1 (1 + 3x)^(−2) = 1+ (−2)(3x) + ((−2(−3))/(2!)) (3x)^2 + ((−2(−3)(−4))/(3!))(3x)^3 +... for ∣3x∣ < 1 = 1 − 6x + 9x^2 −216x^3 + ... for −(1/3) < x < (1/3) For this series to converge, −(1/3) < x<(1/3) (2) (1−x)^(−1) = 1 + (−1)(−x) + ((−1(−2))/(2!)) (−x)^2 + ((−1(−2)(−3))/(3!))(−x)^3 +.... for∣−x∣ <1 = 1+ x + x^2 + x^3 +... for −1 < x < 1 For this series to converge, −1 < x < 1. you don′t need to force this series in terms of (1/x) . It automatically happens.

$$\:\left(\mathrm{1}\right)\:\mathrm{Generally},\:\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} \:=\:\mathrm{1}\:+\:{nx}\:+\:\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}\:{x}^{\mathrm{2}} \:+\:\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} \:+\:...... \\ $$$$\mathrm{valid}\:\mathrm{for}\:\left(\mathrm{converges}\:\mathrm{for}\right)\:=\:\mid{x}\mid<\mathrm{1} \\ $$$$\left(\mathrm{1}\:+\:\mathrm{3}{x}\right)^{−\mathrm{2}} \:=\:\mathrm{1}+\:\left(−\mathrm{2}\right)\left(\mathrm{3}{x}\right)\:+\:\frac{−\mathrm{2}\left(−\mathrm{3}\right)}{\mathrm{2}!}\:\left(\mathrm{3}{x}\right)^{\mathrm{2}} \:+\:\frac{−\mathrm{2}\left(−\mathrm{3}\right)\left(−\mathrm{4}\right)}{\mathrm{3}!}\left(\mathrm{3}{x}\right)^{\mathrm{3}} \:+...\:\mathrm{for}\:\mid\mathrm{3}{x}\mid\:<\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}\:−\:\mathrm{6}{x}\:+\:\mathrm{9}{x}^{\mathrm{2}} \:−\mathrm{216}{x}^{\mathrm{3}} \:+\:...\:\mathrm{for}\:\:−\frac{\mathrm{1}}{\mathrm{3}}\:<\:{x}\:<\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{For}\:\mathrm{this}\:\mathrm{series}\:\mathrm{to}\:\mathrm{converge},\:\:\:−\frac{\mathrm{1}}{\mathrm{3}}\:<\:{x}<\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\left(\mathrm{2}\right)\:\left(\mathrm{1}−{x}\right)^{−\mathrm{1}} \:=\:\mathrm{1}\:+\:\left(−\mathrm{1}\right)\left(−{x}\right)\:+\:\frac{−\mathrm{1}\left(−\mathrm{2}\right)}{\mathrm{2}!}\:\left(−{x}\right)^{\mathrm{2}} +\:\frac{−\mathrm{1}\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)}{\mathrm{3}!}\left(−{x}\right)^{\mathrm{3}} \:+....\:\mathrm{for}\mid−{x}\mid\:<\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}+\:{x}\:+\:{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{3}} \:+...\:\mathrm{for}\:\:−\mathrm{1}\:<\:{x}\:<\:\mathrm{1} \\ $$$$\mathrm{For}\:\mathrm{this}\:\mathrm{series}\:\mathrm{to}\:\mathrm{converge},\:−\mathrm{1}\:<\:{x}\:<\:\mathrm{1}. \\ $$$$\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\:\mathrm{to}\:\mathrm{force}\:\mathrm{this}\:\mathrm{series}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\frac{\mathrm{1}}{{x}}\:.\:\mathrm{It}\:\mathrm{automatically}\:\mathrm{happens}. \\ $$

Commented by aurpeyz last updated on 28/Aug/20

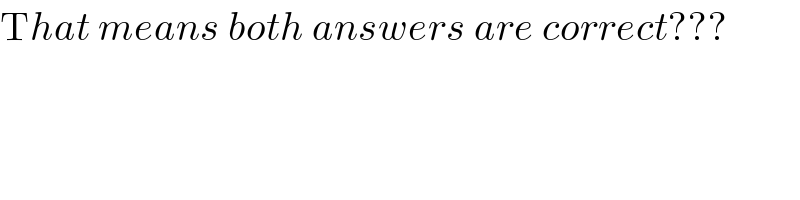
That means both answers are correct???

$$\mathrm{T}{hat}\:{means}\:{both}\:{answers}\:{are}\:{correct}??? \\ $$

Commented by Rio Michael last updated on 28/Aug/20

exactly

$$\mathrm{exactly} \\ $$

Commented by aurpeyz last updated on 30/Aug/20

Thanks alot Rio Micheal

$$\mathrm{T}{hanks}\:{alot}\:{Rio}\:{Micheal} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com