Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 110182 by udaythool last updated on 27/Aug/20

$$\mathrm{Solve}{x}^3+15x-92=0$$

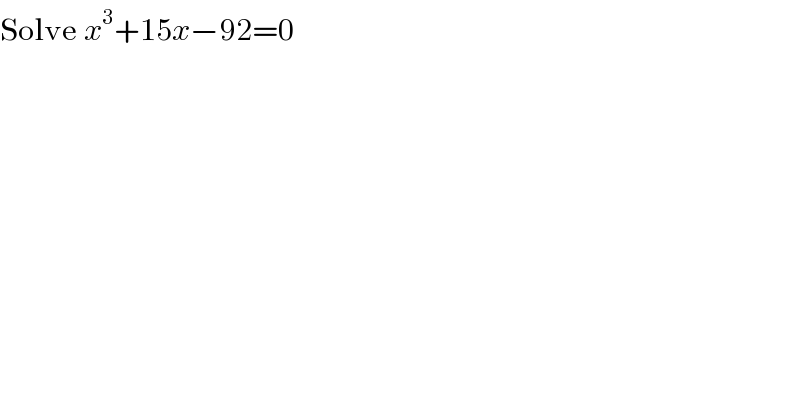
Commented by mr W last updated on 27/Aug/20

$$letx=u+v$$$${(u+v)}^3+15(u+v)-92=0$$$$u^3+v^3+3(uv+5)(u+v)-92=0$$$$letuv+5=0\Rightarrow uv=-5\Rightarrow u^3{v}^3=-125$$$$\Rightarrow u^3+v^3-92=0\Rightarrow u^3+v^3=92$$$$u^{3}and{v}^{3}arerootsof{z}^2-92z-125=0$$$$\Rightarrow z=46\pm \sqrt{{46}^2+125}=46\pm 3\sqrt{249}$$$$\Rightarrow u=\sqrt[3]{46+3\sqrt{249}}$$$$\Rightarrow v=\sqrt[3]{46-3\sqrt{249}}$$$$\Rightarrow x=\sqrt[3]{46+3\sqrt{249}}+\sqrt[3]{46-3\sqrt{249}}\approx 3.4339$$

Commented by udaythool last updated on 28/Aug/20

��THANKS��

Answered by 1549442205PVT last updated on 28/Aug/20

$$\mathrm{Put}\mathrm{x}=\sqrt{5}\mathrm{y}\Rightarrow 5\sqrt{5}{\mathrm{y}}^3+15\sqrt{5}\mathrm{y}-92=0$$$$\iff {\mathrm{y}}^3+3\mathrm{y}-\frac{92}{5\sqrt{5}}=0\left(1\right)$$$$\mathrm{Put}\mathrm{y}=\mathrm{z}-\frac{1}{\mathrm{z}}\Rightarrow {\mathrm{y}}^3={\mathrm{z}}^3-\frac{1}{{\mathrm{z}}^3}-3(\mathrm{z}-\frac{1}{\mathrm{z}})$$$$\mathrm{Replace}\mathrm{into}\left(1\right)\mathrm{we}\mathrm{get}$$$${\mathrm{z}}^3-\frac{1}{{\mathrm{z}}^3}-\frac{92\sqrt{5}}{25}=0\iff {\mathrm{z}}^6-\frac{92\sqrt{5}}{25}{\mathrm{z}}^3-1=0$$$$\text{Prime causes double exponent: use braces to clarify}$$$$\mathrm{\Delta }={\left(\frac{92\sqrt{5}}{25}\right)}^2+4=\frac{8464}{125}+4=\frac{8964}{125}$$$$\Rightarrow {\mathrm{z}}^3=\frac{\frac{92\sqrt{5}}{25}\pm \frac{6\sqrt{1245}}{25}}{2}=\frac{92\sqrt{5}\pm 6\sqrt{1245}}{50}$$$$\mathrm{i})\mathrm{For}{\mathrm{z}}^3=\frac{92\sqrt{5}+6\sqrt{1245}}{50}.$$$$\mathrm{Since}(\mathrm{a}-\mathrm{b})(\mathrm{a}+\mathrm{b})={\mathrm{a}}^2-{\mathrm{b}}^2,\mathrm{we}\mathrm{have}$$$$\frac{92\sqrt{5}+6\sqrt{1245}}{50}\times \frac{92\sqrt{5}-6\sqrt{1245}}{50}=-1(\ast )$$$$\mathrm{Hence},.\mathrm{By}{\mathrm{Vieta}}^{\prime }\mathrm{s}\mathrm{theorem}\mathrm{we}\mathrm{get}$$$$\mathrm{z}={}^3\sqrt{\frac{92\sqrt{5}+6\sqrt{1245}}{50}},-\frac{1}{\mathrm{z}}={}^3\sqrt{\frac{92\sqrt{5}-6\sqrt{1245}}{50}}$$$$\Rightarrow \mathrm{x}=\sqrt{5}\mathrm{y}=\sqrt{5}(\mathrm{z}-\frac{1}{\mathrm{z}})=$$$$\sqrt{5}({}^3\sqrt{\frac{92\sqrt{5}+6\sqrt{1245}}{50}}+{}^3\sqrt{\frac{92\sqrt{5}-6\sqrt{1245}}{50}})$$$$={}^3\sqrt{\frac{2300+150\sqrt{249}}{50}}+{}^3\sqrt{\frac{2300-150\sqrt{249}}{50}}$$$$=={}^3\sqrt{46+3\sqrt{249}}+{}^3\sqrt{46-3\sqrt{249}}$$$$\mathrm{ii})\mathrm{For}{\mathrm{z}}^3={}^3\sqrt{\frac{92\sqrt{5}-6\sqrt{1245}}{50}}.\mathrm{From}(\ast )$$$$\mathrm{we}\mathrm{infer}\mathrm{z}-\frac{1}{\mathrm{z}}\mathrm{is}\mathrm{the}\mathrm{same}\mathrm{value}$$$$\mathrm{Thus},\mathrm{given}\mathrm{equation}{\mathrm{x}}^3+15\mathrm{x}-92=0$$$$\mathrm{has}\mathrm{unique}\mathrm{root}$$$$\mathbf{x}={}^3\sqrt{46+3\sqrt{249}}+{}^3\sqrt{46-3\sqrt{249}}$$

Commented by udaythool last updated on 28/Aug/20

Really I enjoyed this approach. Thanks �� ����

Terms of Service

Privacy Policy

Contact: info@tinkutara.com