Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 110214 by mathdave last updated on 27/Aug/20

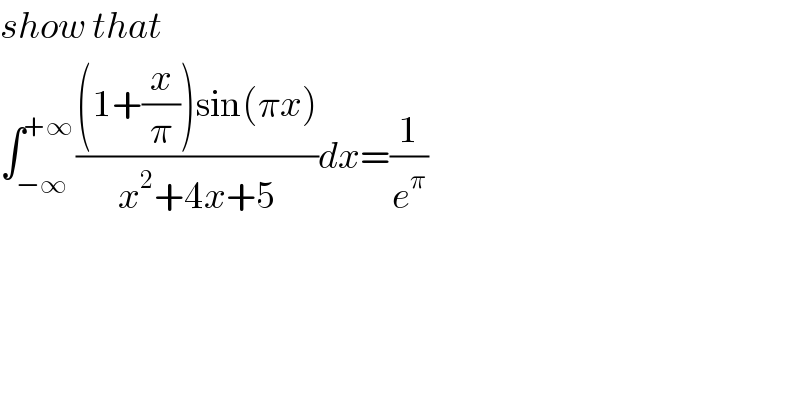
show that ∫_(−∞) ^(+∞) (((1+(x/π))sin(πx))/(x^2 +4x+5))dx=(1/e^π )

$${show}\:{that}\: \\ $$$$\int_{−\infty} ^{+\infty} \frac{\left(\mathrm{1}+\frac{{x}}{\pi}\right)\mathrm{sin}\left(\pi{x}\right)}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{5}}{dx}=\frac{\mathrm{1}}{{e}^{\pi} } \\ $$

Answered by mathmax by abdo last updated on 27/Aug/20

I =∫_(−∞) ^(+∞) (((1+(x/π))sin(πx))/(x^2 +4x +5))=Im(∫_(−∞) ^(+∞) (((1+(x/π))e^(iπx) )/(x^2 +4x+5))) let condider the complex function ϕ(z) =(((1+(z/π))e^(iπz) )/(z^2 +4z +5)) poles of ϕ? z^2 +4z +5 =0→Δ^′ =4−5 =−1 ⇒z_1 =−2+i and z_2 =−2−i residus theorem ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπRes(ϕ,−2+i) we have ϕ(z) =(((1+(z/π))e^(iπz) )/((z−z_1 )(z−z_2 ))) ⇒Res(ϕ,−2+i) = =lim_(z→z_1 ) (z−z_1 )ϕ(z) = (((1+(z_1 /π))e^(iπz_1 ) )/(2i)) =(((1+((−2+i)/π))e^(iπ(−2+i)) )/(2i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ×(((π−2+i)e^(−π) )/(2iπ)) =(π−2 +i)e^(−π) =(π−2)e^(−π) +i e^(−π) ⇒ Im(∫....) = e^(−π) ⇒★ I =(1/e^π )★

$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\frac{\left(\mathrm{1}+\frac{\mathrm{x}}{\pi}\right)\mathrm{sin}\left(\pi\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4x}\:+\mathrm{5}}=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\left(\mathrm{1}+\frac{\mathrm{x}}{\pi}\right)\mathrm{e}^{\mathrm{i}\pi\mathrm{x}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{5}}\right)\:\:\mathrm{let}\:\mathrm{condider}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{function} \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\left(\mathrm{1}+\frac{\mathrm{z}}{\pi}\right)\mathrm{e}^{\mathrm{i}\pi\mathrm{z}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{4z}\:+\mathrm{5}}\:\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{2}} \:+\mathrm{4z}\:+\mathrm{5}\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{4}−\mathrm{5}\:=−\mathrm{1}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{2}+\mathrm{i}\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{2}−\mathrm{i} \\ $$$$\mathrm{residus}\:\mathrm{theorem}\:\Rightarrow\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\varphi,−\mathrm{2}+\mathrm{i}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\varphi\left(\mathrm{z}\right)\:=\frac{\left(\mathrm{1}+\frac{\mathrm{z}}{\pi}\right)\mathrm{e}^{\mathrm{i}\pi\mathrm{z}} }{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:\Rightarrow\mathrm{Res}\left(\varphi,−\mathrm{2}+\mathrm{i}\right)\:= \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } \left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\varphi\left(\mathrm{z}\right)\:=\:\:\frac{\left(\mathrm{1}+\frac{\mathrm{z}_{\mathrm{1}} }{\pi}\right)\mathrm{e}^{\mathrm{i}\pi\mathrm{z}_{\mathrm{1}} } }{\mathrm{2i}}\:=\frac{\left(\mathrm{1}+\frac{−\mathrm{2}+\mathrm{i}}{\pi}\right)\mathrm{e}^{\mathrm{i}\pi\left(−\mathrm{2}+\mathrm{i}\right)} }{\mathrm{2i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\left(\pi−\mathrm{2}+\mathrm{i}\right)\mathrm{e}^{−\pi} }{\mathrm{2i}\pi}\:=\left(\pi−\mathrm{2}\:+\mathrm{i}\right)\mathrm{e}^{−\pi} \\ $$$$=\left(\pi−\mathrm{2}\right)\mathrm{e}^{−\pi} \:+\mathrm{i}\:\mathrm{e}^{−\pi} \:\Rightarrow\:\mathrm{Im}\left(\int....\right)\:=\:\mathrm{e}^{−\pi} \:\Rightarrow\bigstar\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{e}^{\pi} }\bigstar \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com