Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 110299 by Lekhraj last updated on 28/Aug/20

Answered by Her_Majesty last updated on 28/Aug/20

5x+5y=2xy ⇒ 5∣xy ⇒ 5∣x∨5∣y let x=5k 25k+5y=10ky y=((5k)/(2k−1)) k=1 ⇒ y=5∧x=5 but x≠y k=3 ⇒ y=3∧x=15 ⇒ (√(x+y))=3(√2) only solution because ((5k)/(2k−1))>2∀k>0 of course x=3∧y=15 is the 2^(nd) possibility but it also leads to (√(x+y))=3(√2)

$$\mathrm{5}{x}+\mathrm{5}{y}=\mathrm{2}{xy} \\ $$$$\Rightarrow\:\mathrm{5}\mid{xy}\:\Rightarrow\:\mathrm{5}\mid{x}\vee\mathrm{5}\mid{y} \\ $$$${let}\:{x}=\mathrm{5}{k} \\ $$$$\mathrm{25}{k}+\mathrm{5}{y}=\mathrm{10}{ky} \\ $$$${y}=\frac{\mathrm{5}{k}}{\mathrm{2}{k}−\mathrm{1}} \\ $$$${k}=\mathrm{1}\:\Rightarrow\:{y}=\mathrm{5}\wedge{x}=\mathrm{5}\:{but}\:{x}\neq{y} \\ $$$${k}=\mathrm{3}\:\Rightarrow\:{y}=\mathrm{3}\wedge{x}=\mathrm{15}\:\Rightarrow\:\sqrt{{x}+{y}}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$${only}\:{solution}\:{because}\:\frac{\mathrm{5}{k}}{\mathrm{2}{k}−\mathrm{1}}>\mathrm{2}\forall{k}>\mathrm{0} \\ $$$${of}\:{course}\:{x}=\mathrm{3}\wedge{y}=\mathrm{15}\:{is}\:{the}\:\mathrm{2}^{{nd}} \:{possibility} \\ $$$${but}\:{it}\:{also}\:{leads}\:{to}\:\sqrt{{x}+{y}}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$

Commented by Lekhraj last updated on 28/Aug/20

Thanks

$$\mathrm{Thanks} \\ $$

Commented by udaythool last updated on 28/Aug/20

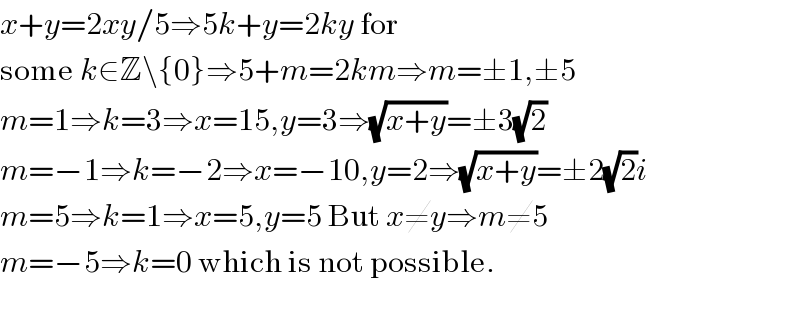
x+y=2xy/5⇒5k+y=2ky for some k∈Z\{0}⇒5+m=2km⇒m=±1,±5 m=1⇒k=3⇒x=15,y=3⇒(√(x+y))=±3(√2) m=−1⇒k=−2⇒x=−10,y=2⇒(√(x+y))=±2(√2)i m=5⇒k=1⇒x=5,y=5 But x≠y⇒m≠5 m=−5⇒k=0 which is not possible.

$${x}+{y}=\mathrm{2}{xy}/\mathrm{5}\Rightarrow\mathrm{5}{k}+{y}=\mathrm{2}{ky}\:\mathrm{for} \\ $$$$\mathrm{some}\:{k}\in\mathbb{Z}\backslash\left\{\mathrm{0}\right\}\Rightarrow\mathrm{5}+{m}=\mathrm{2}{km}\Rightarrow{m}=\pm\mathrm{1},\pm\mathrm{5} \\ $$$${m}=\mathrm{1}\Rightarrow{k}=\mathrm{3}\Rightarrow{x}=\mathrm{15},{y}=\mathrm{3}\Rightarrow\sqrt{{x}+{y}}=\pm\mathrm{3}\sqrt{\mathrm{2}} \\ $$$${m}=−\mathrm{1}\Rightarrow{k}=−\mathrm{2}\Rightarrow{x}=−\mathrm{10},{y}=\mathrm{2}\Rightarrow\sqrt{{x}+{y}}=\pm\mathrm{2}\sqrt{\mathrm{2}}{i} \\ $$$${m}=\mathrm{5}\Rightarrow{k}=\mathrm{1}\Rightarrow{x}=\mathrm{5},{y}=\mathrm{5}\:\mathrm{But}\:{x}\neq{y}\Rightarrow{m}\neq\mathrm{5} \\ $$$${m}=−\mathrm{5}\Rightarrow{k}=\mathrm{0}\:\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{possible}. \\ $$$$ \\ $$

Commented by Her_Majesty last updated on 28/Aug/20

the question says “distinct positive integers” so as I stated, there′s only one solution

$${the}\:{question}\:{says}\:``{distinct}\:{positive}\:{integers}'' \\ $$$${so}\:{as}\:{I}\:{stated},\:{there}'{s}\:{only}\:{one}\:{solution} \\ $$

Commented by Rasheed.Sindhi last updated on 28/Aug/20

(√(x+y))=±3(√2) is not correct,I think. Because the symbol “(√( )) ”is used for positive square root only. For both roots “±(√( ))”is used.(And for negative root “−(√( ))”is used.)

$$\sqrt{{x}+{y}}=\pm\mathrm{3}\sqrt{\mathrm{2}}\:\:{is}\:{not}\:{correct},{I}\:{think}. \\ $$$${Because}\:{the}\:{symbol}\:``\sqrt{\:\:\:\:}\:''{is} \\ $$$${used}\:{for}\:{positive}\:{square}\:{root} \\ $$$${only}.\:{For}\:{both}\:{roots}\:``\pm\sqrt{\:\:\:\:}''{is} \\ $$$${used}.\left({And}\:{for}\:{negative}\:{root}\:\right. \\ $$$$\left.``−\sqrt{\:\:\:\:}''{is}\:{used}.\right) \\ $$

Commented by Her_Majesty last updated on 28/Aug/20

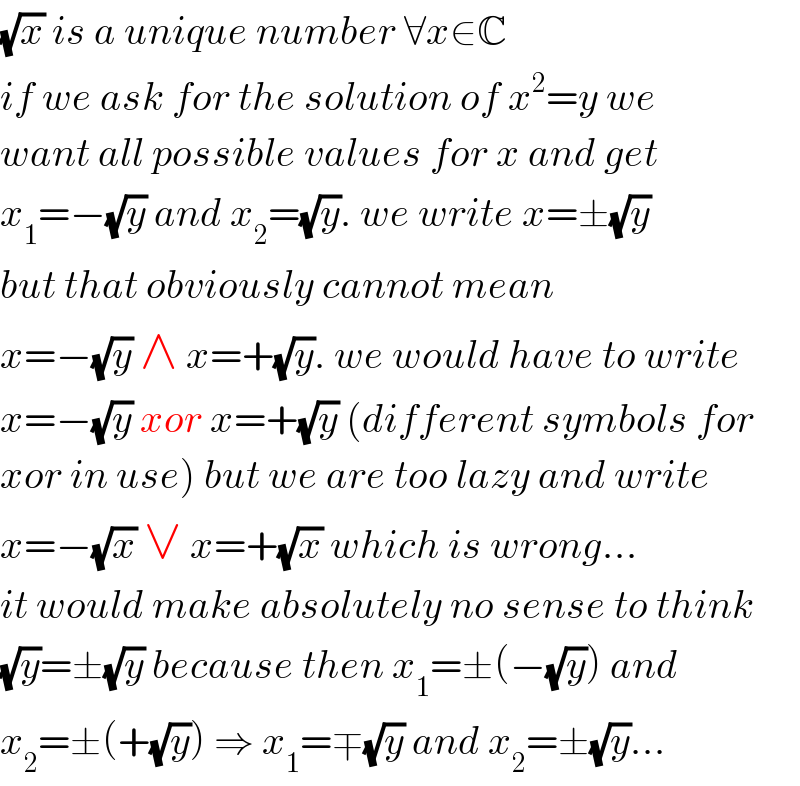
(√x) is a unique number ∀x∈C if we ask for the solution of x^2 =y we want all possible values for x and get x_1 =−(√y) and x_2 =(√y). we write x=±(√y) but that obviously cannot mean x=−(√y) ∧ x=+(√y). we would have to write x=−(√y) xor x=+(√y) (different symbols for xor in use) but we are too lazy and write x=−(√x) ∨ x=+(√x) which is wrong... it would make absolutely no sense to think (√y)=±(√y) because then x_1 =±(−(√y)) and x_2 =±(+(√y)) ⇒ x_1 =∓(√y) and x_2 =±(√y)...

$$\sqrt{{x}}\:{is}\:{a}\:{unique}\:{number}\:\forall{x}\in\mathbb{C} \\ $$$${if}\:{we}\:{ask}\:{for}\:{the}\:{solution}\:{of}\:{x}^{\mathrm{2}} ={y}\:{we} \\ $$$${want}\:{all}\:{possible}\:{values}\:{for}\:{x}\:{and}\:{get} \\ $$$${x}_{\mathrm{1}} =−\sqrt{{y}}\:{and}\:{x}_{\mathrm{2}} =\sqrt{{y}}.\:{we}\:{write}\:{x}=\pm\sqrt{{y}} \\ $$$${but}\:{that}\:{obviously}\:{cannot}\:{mean} \\ $$$${x}=−\sqrt{{y}}\:\wedge\:{x}=+\sqrt{{y}}.\:{we}\:{would}\:{have}\:{to}\:{write} \\ $$$${x}=−\sqrt{{y}}\:{xor}\:{x}=+\sqrt{{y}}\:\left({different}\:{symbols}\:{for}\right. \\ $$$$\left.{xor}\:{in}\:{use}\right)\:{but}\:{we}\:{are}\:{too}\:{lazy}\:{and}\:{write} \\ $$$${x}=−\sqrt{{x}}\:\vee\:{x}=+\sqrt{{x}}\:{which}\:{is}\:{wrong}... \\ $$$${it}\:{would}\:{make}\:{absolutely}\:{no}\:{sense}\:{to}\:{think} \\ $$$$\sqrt{{y}}=\pm\sqrt{{y}}\:{because}\:{then}\:{x}_{\mathrm{1}} =\pm\left(−\sqrt{{y}}\right)\:{and} \\ $$$${x}_{\mathrm{2}} =\pm\left(+\sqrt{{y}}\right)\:\Rightarrow\:{x}_{\mathrm{1}} =\mp\sqrt{{y}}\:{and}\:{x}_{\mathrm{2}} =\pm\sqrt{{y}}... \\ $$

Commented by udaythool last updated on 28/Aug/20

Oh! Yes, I haven′t noticed...

$$\mathrm{Oh}! \\ $$$$\mathrm{Yes},\:\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{noticed}... \\ $$

Answered by Rasheed.Sindhi last updated on 28/Aug/20

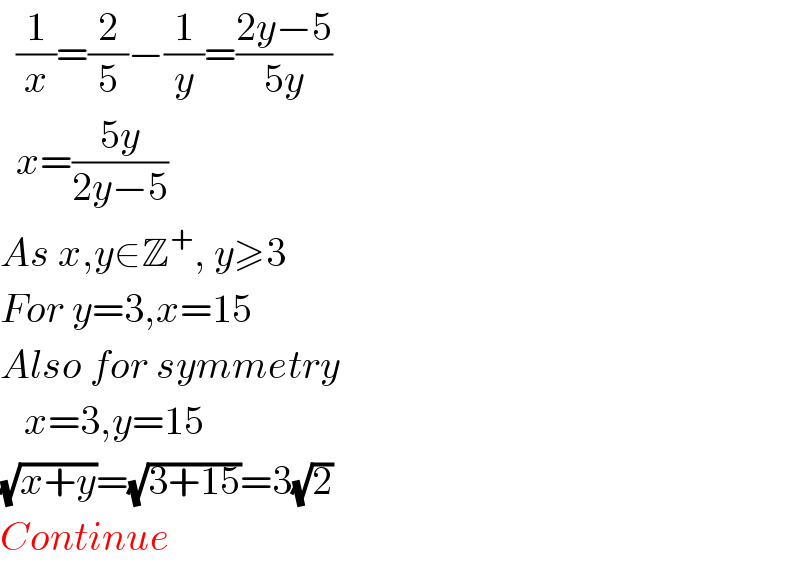
(1/x)=(2/5)−(1/y)=((2y−5)/(5y)) x=((5y)/(2y−5)) As x,y∈Z^+ , y≥3 For y=3,x=15 Also for symmetry x=3,y=15 (√(x+y))=(√(3+15))=3(√2) Continue

$$\:\:\frac{\mathrm{1}}{{x}}=\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{1}}{{y}}=\frac{\mathrm{2}{y}−\mathrm{5}}{\mathrm{5}{y}} \\ $$$$\:\:{x}=\frac{\mathrm{5}{y}}{\mathrm{2}{y}−\mathrm{5}} \\ $$$${As}\:{x},{y}\in\mathbb{Z}^{+} ,\:{y}\geqslant\mathrm{3} \\ $$$${For}\:{y}=\mathrm{3},{x}=\mathrm{15} \\ $$$${Also}\:{for}\:{symmetry} \\ $$$$\:\:\:{x}=\mathrm{3},{y}=\mathrm{15} \\ $$$$\sqrt{{x}+{y}}=\sqrt{\mathrm{3}+\mathrm{15}}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$${Continue} \\ $$

Commented by Lekhraj last updated on 28/Aug/20

Thanks

$$\mathrm{Thanks} \\ $$

Answered by 1549442205PVT last updated on 29/Aug/20

(1/x)+(1/y)=(2/5)⇔((x+y)/(xy))=(2/5)⇔2xy=5(x+y) ⇔4xy−10(x+y)+25=25 ⇔(2x−5)(2y−5)=25 (1)⇒(2x−5 )is an odd divisor of 25 ⇒2x−5∈{1,−1,5,−5,−25,25} i)2x−5=1⇒x=3 .Replace into (1) we get y=15 ii)2x−5=−1⇒x=2.Replace into (1)we get y=−10 ∉Z^+ ⇒rejected iii)2x−5=5⇒x=5.Replace into (1) we get y=5 iv)2x−5=−25⇒x=−10⇒rejected v)2x−5=25⇒x=15⇒y=3 Combinating all above cases we get (x,y)∈{(3,15),(5,5),(15,3)} ⇒(√(x+y)) ∈{3(√2) ,(√(10))}

$$\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}=\frac{\mathrm{2}}{\mathrm{5}}\Leftrightarrow\frac{\mathrm{x}+\mathrm{y}}{\mathrm{xy}}=\frac{\mathrm{2}}{\mathrm{5}}\Leftrightarrow\mathrm{2xy}=\mathrm{5}\left(\mathrm{x}+\mathrm{y}\right) \\ $$$$\Leftrightarrow\mathrm{4xy}−\mathrm{10}\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{25}=\mathrm{25} \\ $$$$\Leftrightarrow\left(\mathrm{2x}−\mathrm{5}\right)\left(\mathrm{2y}−\mathrm{5}\right)=\mathrm{25}\:\:\left(\mathrm{1}\right)\Rightarrow\left(\mathrm{2x}−\mathrm{5}\:\right)\mathrm{is} \\ $$$$\mathrm{an}\:\mathrm{odd}\:\mathrm{divisor}\:\mathrm{of}\:\mathrm{25} \\ $$$$\Rightarrow\mathrm{2x}−\mathrm{5}\in\left\{\mathrm{1},−\mathrm{1},\mathrm{5},−\mathrm{5},−\mathrm{25},\mathrm{25}\right\} \\ $$$$\left.\mathrm{i}\right)\mathrm{2x}−\mathrm{5}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{3}\:.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right)\:\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{y}=\mathrm{15} \\ $$$$\left.\mathrm{ii}\right)\mathrm{2x}−\mathrm{5}=−\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{2}.\mathrm{Replace}\:\mathrm{into} \\ $$$$\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{get}\:\mathrm{y}=−\mathrm{10}\:\notin\mathbb{Z}^{+} \Rightarrow\mathrm{rejected} \\ $$$$\left.\mathrm{iii}\right)\mathrm{2x}−\mathrm{5}=\mathrm{5}\Rightarrow\mathrm{x}=\mathrm{5}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{y}=\mathrm{5} \\ $$$$\left.\mathrm{iv}\right)\mathrm{2x}−\mathrm{5}=−\mathrm{25}\Rightarrow\mathrm{x}=−\mathrm{10}\Rightarrow\mathrm{rejected} \\ $$$$\left.\mathrm{v}\right)\mathrm{2x}−\mathrm{5}=\mathrm{25}\Rightarrow\mathrm{x}=\mathrm{15}\Rightarrow\mathrm{y}=\mathrm{3} \\ $$$$\mathrm{Combinating}\:\mathrm{all}\:\mathrm{above}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)\in\left\{\left(\mathrm{3},\mathrm{15}\right),\left(\mathrm{5},\mathrm{5}\right),\left(\mathrm{15},\mathrm{3}\right)\right\} \\ $$$$\Rightarrow\sqrt{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}\:\in\left\{\mathrm{3}\sqrt{\mathrm{2}}\:,\sqrt{\mathrm{10}}\right\} \\ $$

Commented by Her_Majesty last updated on 29/Aug/20

saying it again, we′re searching for distinct integers ⇒ x≠y

$${saying}\:{it}\:{again},\:{we}'{re}\:{searching}\:{for}\:{distinct} \\ $$$${integers}\:\Rightarrow\:{x}\neq{y} \\ $$

Commented by Rasheed.Sindhi last updated on 29/Aug/20

Nice Sir! Only exclude (5,5) because they are not distinct. You′ve given the problem usefull form: (2x−5)(2y−5)=25 This form offers limited trials!

$${Nice}\:{Sir}! \\ $$$${Only}\:{exclude}\:\left(\mathrm{5},\mathrm{5}\right)\:{because}\:{they} \\ $$$${are}\:{not}\:\boldsymbol{{distinct}}. \\ $$$${You}'{ve}\:{given}\:{the}\:{problem}\:{usefull} \\ $$$${form}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2x}−\mathrm{5}\right)\left(\mathrm{2y}−\mathrm{5}\right)=\mathrm{25} \\ $$$$\mathcal{T}{his}\:{form}\:{offers}\:{limited}\:{trials}! \\ $$

Commented by 1549442205PVT last updated on 30/Aug/20

Thank Sir.I don′t note that hypothesis .

$$\mathrm{Thank}\:\mathrm{Sir}.\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{note}\:\mathrm{that} \\ $$$$\mathrm{hypothesis}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com