Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 110374 by Aina Samuel Temidayo last updated on 28/Aug/20

If P(x) is a polynomial whose sum of coefficients is 3 and P(x) can be factorised into two polynomials Q(x),R(x) with integer coefficients, the sum of the coefficients Q(x)^2 +R(x)^2 is

$$\mathrm{If}\:\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{whose}\:\mathrm{sum}\:\mathrm{of} \\ $$$$\mathrm{coefficients}\:\mathrm{is}\:\mathrm{3}\:\mathrm{and}\:\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{factorised}\:\mathrm{into}\:\mathrm{two}\:\mathrm{polynomials} \\ $$$$\mathrm{Q}\left(\mathrm{x}\right),\mathrm{R}\left(\mathrm{x}\right)\:\mathrm{with}\:\mathrm{integer}\:\mathrm{coefficients}, \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{coefficients} \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} +\mathrm{R}\left(\mathrm{x}\right)^{\mathrm{2}} \:\mathrm{is} \\ $$

Answered by mr W last updated on 28/Aug/20

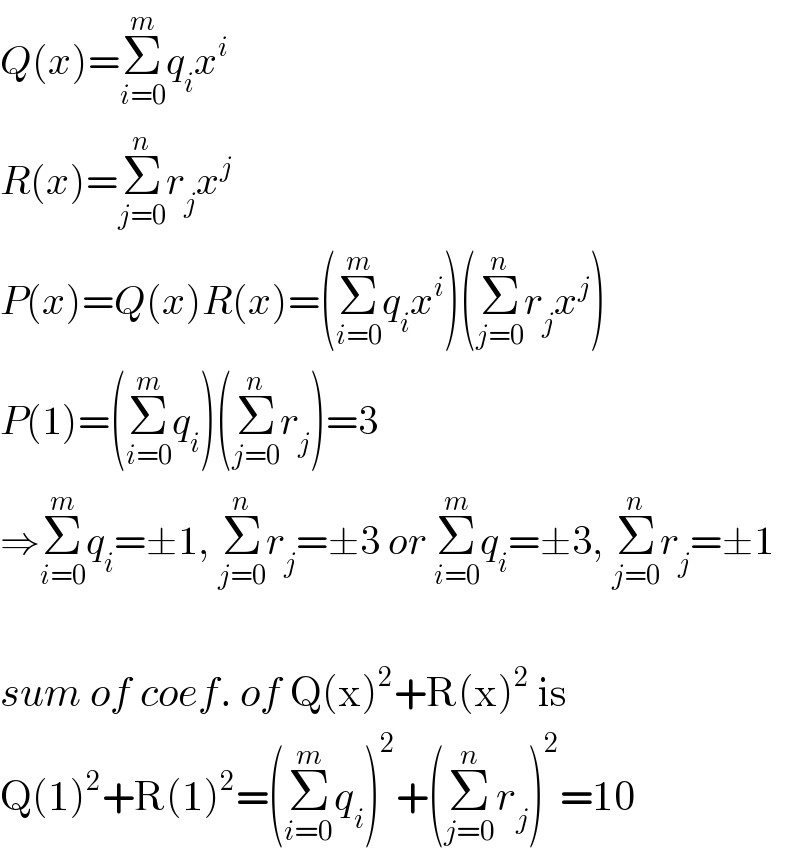
Q(x)=Σ_(i=0) ^m q_i x^i R(x)=Σ_(j=0) ^n r_j x^j P(x)=Q(x)R(x)=(Σ_(i=0) ^m q_i x^i )(Σ_(j=0) ^n r_j x^j ) P(1)=(Σ_(i=0) ^m q_i )(Σ_(j=0) ^n r_j )=3 ⇒Σ_(i=0) ^m q_i =±1, Σ_(j=0) ^n r_j =±3 or Σ_(i=0) ^m q_i =±3, Σ_(j=0) ^n r_j =±1 sum of coef. of Q(x)^2 +R(x)^2 is Q(1)^2 +R(1)^2 =(Σ_(i=0) ^m q_i )^2 +(Σ_(j=0) ^n r_j )^2 =10

$${Q}\left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{q}_{{i}} {x}^{{i}} \\ $$$${R}\left({x}\right)=\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{r}_{{j}} {x}^{{j}} \\ $$$${P}\left({x}\right)={Q}\left({x}\right){R}\left({x}\right)=\left(\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{q}_{{i}} {x}^{{i}} \right)\left(\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{r}_{{j}} {x}^{{j}} \right) \\ $$$${P}\left(\mathrm{1}\right)=\left(\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{q}_{{i}} \right)\left(\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{r}_{{j}} \right)=\mathrm{3} \\ $$$$\Rightarrow\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{q}_{{i}} =\pm\mathrm{1},\:\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{r}_{{j}} =\pm\mathrm{3}\:{or}\:\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{q}_{{i}} =\pm\mathrm{3},\:\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{r}_{{j}} =\pm\mathrm{1} \\ $$$$ \\ $$$${sum}\:{of}\:{coef}.\:{of}\:\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} +\mathrm{R}\left(\mathrm{x}\right)^{\mathrm{2}} \:\mathrm{is} \\ $$$$\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} +\mathrm{R}\left(\mathrm{1}\right)^{\mathrm{2}} =\left(\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{q}_{{i}} \right)^{\mathrm{2}} +\left(\underset{{j}=\mathrm{0}} {\overset{{n}} {\sum}}{r}_{{j}} \right)^{\mathrm{2}} =\mathrm{10} \\ $$

Commented by Aina Samuel Temidayo last updated on 28/Aug/20

Thanks.

$$\mathrm{Thanks}. \\ $$

Answered by floor(10²Eta[1]) last updated on 28/Aug/20

P(1)=3 P(x)=Q(x).R(x) F(x)=Q(x)^2 +R(x)^2 F(1)=Q(1)^2 +R(1)^2 Q(x)=((P(x))/(R(x)))∴Q(x)^2 =((P(x)^2 )/(R(x)^2 )) ⇒Q(1)^2 =((R(1)^2 )/(P(1)^2 ))∴Q(1)^2 =((R(1)^2 )/9) F(1)=R(1)^2 .((10)/9) since Q(x) and R(x) ∈ Z[x] ⇒the sum of coefficients of these polynomials also have to be an integer. so 3=R(1).Q(1) ⇒R(1)=3 and Q(1)=1 or R(1)=1 and Q(1)=3 or R(1)=−1 and Q(1)=−3 or R(1)=−3 and Q(1)=−1 ∴F(1)=((10)/9)R(1)^2 =10 or ((10)/9) but F(x) ∈ Z[x] because F(x)=Q(x)^2 +R(x)^2 so F(1)∈Z⇒F(1)=10

$$\mathrm{P}\left(\mathrm{1}\right)=\mathrm{3} \\ $$$$\mathrm{P}\left(\mathrm{x}\right)=\mathrm{Q}\left(\mathrm{x}\right).\mathrm{R}\left(\mathrm{x}\right) \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} +\mathrm{R}\left(\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{F}\left(\mathrm{1}\right)=\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} +\mathrm{R}\left(\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)=\frac{\mathrm{P}\left(\mathrm{x}\right)}{\mathrm{R}\left(\mathrm{x}\right)}\therefore\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} =\frac{\mathrm{P}\left(\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{R}\left(\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{R}\left(\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{P}\left(\mathrm{1}\right)^{\mathrm{2}} }\therefore\mathrm{Q}\left(\mathrm{1}\right)^{\mathrm{2}} =\frac{\mathrm{R}\left(\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\mathrm{F}\left(\mathrm{1}\right)=\mathrm{R}\left(\mathrm{1}\right)^{\mathrm{2}} .\frac{\mathrm{10}}{\mathrm{9}} \\ $$$$\mathrm{since}\:\mathrm{Q}\left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{R}\left(\mathrm{x}\right)\:\in\:\mathbb{Z}\left[\mathrm{x}\right] \\ $$$$\Rightarrow\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{these}\:\mathrm{polynomials} \\ $$$$\mathrm{also}\:\mathrm{have}\:\mathrm{to}\:\mathrm{be}\:\mathrm{an}\:\mathrm{integer}. \\ $$$$\mathrm{so}\:\mathrm{3}=\mathrm{R}\left(\mathrm{1}\right).\mathrm{Q}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{R}\left(\mathrm{1}\right)=\mathrm{3}\:\mathrm{and}\:\mathrm{Q}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{or}\:\mathrm{R}\left(\mathrm{1}\right)=\mathrm{1}\:\mathrm{and}\:\mathrm{Q}\left(\mathrm{1}\right)=\mathrm{3} \\ $$$$\mathrm{or}\:\mathrm{R}\left(\mathrm{1}\right)=−\mathrm{1}\:\mathrm{and}\:\mathrm{Q}\left(\mathrm{1}\right)=−\mathrm{3} \\ $$$$\mathrm{or}\:\mathrm{R}\left(\mathrm{1}\right)=−\mathrm{3}\:\mathrm{and}\:\mathrm{Q}\left(\mathrm{1}\right)=−\mathrm{1} \\ $$$$\therefore\mathrm{F}\left(\mathrm{1}\right)=\frac{\mathrm{10}}{\mathrm{9}}\mathrm{R}\left(\mathrm{1}\right)^{\mathrm{2}} =\mathrm{10}\:\mathrm{or}\:\frac{\mathrm{10}}{\mathrm{9}} \\ $$$$\mathrm{but}\:\mathrm{F}\left(\mathrm{x}\right)\:\in\:\mathbb{Z}\left[\mathrm{x}\right]\:\mathrm{because}\:\mathrm{F}\left(\mathrm{x}\right)=\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{2}} +\mathrm{R}\left(\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{F}\left(\mathrm{1}\right)\in\mathbb{Z}\Rightarrow\mathrm{F}\left(\mathrm{1}\right)=\mathrm{10} \\ $$$$ \\ $$

Commented by Aina Samuel Temidayo last updated on 28/Aug/20

Thanks.

$$\mathrm{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com