Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 110565 by Aina Samuel Temidayo last updated on 29/Aug/20

Let n∈N. Using the formula lcm(a,b) = ((ab)/(gcd(a,b))) and lcm(a,b,c) =lcm(lcm(a,b),c), find all the possible value of ((6•lcm(n,n+1,n+2,n+3))/(n(n+1)(n+2)(n+3)))

$$\mathrm{Let}\:\mathrm{n}\in\mathbb{N}.\:\mathrm{Using}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right) \\ $$$$=\:\frac{\mathrm{ab}}{\mathrm{gcd}\left(\mathrm{a},\mathrm{b}\right)}\:\mathrm{and}\:\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c}\right) \\ $$$$=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{c}\right),\:\mathrm{find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possible} \\ $$$$\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{6}\bullet\mathrm{lcm}\left(\mathrm{n},\mathrm{n}+\mathrm{1},\mathrm{n}+\mathrm{2},\mathrm{n}+\mathrm{3}\right)}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right)} \\ $$

Commented by kaivan.ahmadi last updated on 29/Aug/20

let m=((6.lcm(n,n+1,n+2,n+3))/(n(n+1)(n+2)(n+3))) lcm(n,n+1)=n(n+1)= lcm(n+2,n+3)=(n+2)(n+3) if n=2k⇒lcm(n(n+1),(n+2)(n+3))= lcm(2k(2k+1),2(k+1)(2k+3))=2k(k+1)(2k+1)(2k+3) ⇒m=((12k(k+1)(2k+1)(2k+3))/(4k(2k+1)(k+1)(2k+3)))=3 if n=2k+1⇒lcm(n(n+1),(n+2)(n+3))= lcm(2(2k+1)(k+1),2(2k+3)(k+2))= 2(k+1)(k+2)(2k+1)(2k+3) ⇒m=((12(k+1)(k+2)(2k+1)(2k+3))/(4(2k+1)(k+1)(2k+3)(k+2)))=3 so m=3

$${let}\:{m}=\frac{\mathrm{6}.{lcm}\left({n},{n}+\mathrm{1},{n}+\mathrm{2},{n}+\mathrm{3}\right)}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$${lcm}\left({n},{n}+\mathrm{1}\right)={n}\left({n}+\mathrm{1}\right)= \\ $$$${lcm}\left({n}+\mathrm{2},{n}+\mathrm{3}\right)=\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right) \\ $$$${if}\:{n}=\mathrm{2}{k}\Rightarrow{lcm}\left({n}\left({n}+\mathrm{1}\right),\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)\right)= \\ $$$${lcm}\left(\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{1}\right),\mathrm{2}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)\right)=\mathrm{2}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right) \\ $$$$\Rightarrow{m}=\frac{\mathrm{12}{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)}{\mathrm{4}{k}\left(\mathrm{2}{k}+\mathrm{1}\right)\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)}=\mathrm{3} \\ $$$${if}\:{n}=\mathrm{2}{k}+\mathrm{1}\Rightarrow{lcm}\left({n}\left({n}+\mathrm{1}\right),\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)\right)= \\ $$$${lcm}\left(\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\left({k}+\mathrm{1}\right),\mathrm{2}\left(\mathrm{2}{k}+\mathrm{3}\right)\left({k}+\mathrm{2}\right)\right)= \\ $$$$\mathrm{2}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right) \\ $$$$\Rightarrow{m}=\frac{\mathrm{12}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)}{\mathrm{4}\left(\mathrm{2}{k}+\mathrm{1}\right)\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)\left({k}+\mathrm{2}\right)}=\mathrm{3} \\ $$$${so}\:{m}=\mathrm{3} \\ $$$$ \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

Thanks

$$\mathrm{Thanks} \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

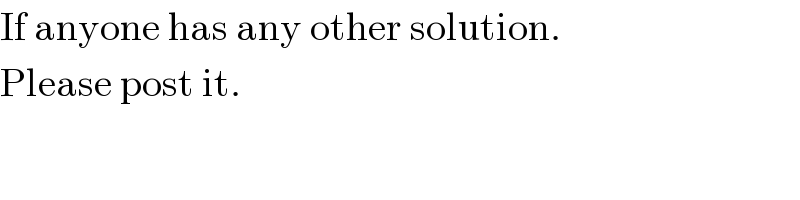
If anyone has any other solution. Please post it.

$$\mathrm{If}\:\mathrm{anyone}\:\mathrm{has}\:\mathrm{any}\:\mathrm{other}\:\mathrm{solution}. \\ $$$$\mathrm{Please}\:\mathrm{post}\:\mathrm{it}. \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

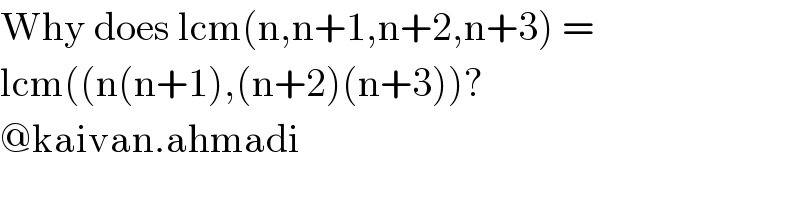
Why does lcm(n,n+1,n+2,n+3) = lcm((n(n+1),(n+2)(n+3))? @kaivan.ahmadi

$$\mathrm{Why}\:\mathrm{does}\:\mathrm{lcm}\left(\mathrm{n},\mathrm{n}+\mathrm{1},\mathrm{n}+\mathrm{2},\mathrm{n}+\mathrm{3}\right)\:= \\ $$$$\mathrm{lcm}\left(\left(\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right),\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right)\right)?\right. \\ $$$$@\mathrm{kaivan}.\mathrm{ahmadi} \\ $$

Commented by floor(10²Eta[1]) last updated on 29/Aug/20

because lcm(a,b,c)=lcm(lcm(a,b),c) the same logic works for 4 numbers: lcm(a,b,c,d)=lcm(lcm(a,b),lcm(c,d)) since n and n+1 are coprimes and n+2 and n+3 also are coprimes so lcm(n, n+1)=n(n+1) and lcm(n+2, n+3)=(n+2)(n+3) so lcm(n, n+1, n+2, n+3)= lcm((n(n+1),(n+2)(n+3))

$$\mathrm{because}\:\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{c}\right) \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{logic}\:\mathrm{works}\:\mathrm{for}\:\mathrm{4}\:\mathrm{numbers}: \\ $$$$\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{lcm}\left(\mathrm{c},\mathrm{d}\right)\right) \\ $$$$\mathrm{since}\:\mathrm{n}\:\mathrm{and}\:\mathrm{n}+\mathrm{1}\:\mathrm{are}\:\mathrm{coprimes}\:\mathrm{and} \\ $$$$\mathrm{n}+\mathrm{2}\:\mathrm{and}\:\mathrm{n}+\mathrm{3}\:\mathrm{also}\:\mathrm{are}\:\mathrm{coprimes}\:\mathrm{so} \\ $$$$\mathrm{lcm}\left(\mathrm{n},\:\mathrm{n}+\mathrm{1}\right)=\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\:\mathrm{and} \\ $$$$\mathrm{lcm}\left(\mathrm{n}+\mathrm{2},\:\mathrm{n}+\mathrm{3}\right)=\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right) \\ $$$$\mathrm{so} \\ $$$$\mathrm{lcm}\left(\mathrm{n},\:\mathrm{n}+\mathrm{1},\:\mathrm{n}+\mathrm{2},\:\mathrm{n}+\mathrm{3}\right)= \\ $$$$\mathrm{lcm}\left(\left(\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right),\left(\mathrm{n}+\mathrm{2}\right)\left(\mathrm{n}+\mathrm{3}\right)\right)\right. \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

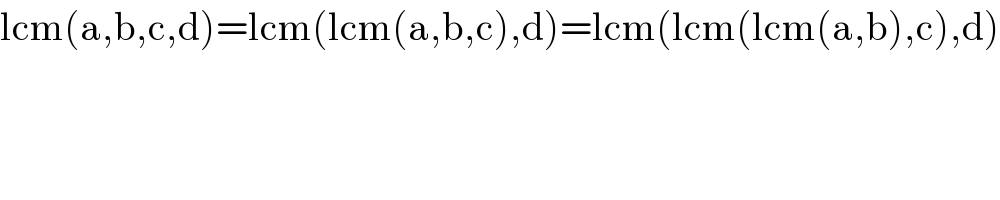
lcm(a,b,c,d)=lcm(lcm(a,b,c),d)=lcm(lcm(lcm(a,b),c),d)

$$\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c}\right),\mathrm{d}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{c}\right),\mathrm{d}\right) \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

I don′t think lcm(a,b,c,d)=lcm(lcm(a,b),lcm(c,d)) is a good argument.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think} \\ $$$$\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{lcm}\left(\mathrm{c},\mathrm{d}\right)\right) \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{good}\:\mathrm{argument}. \\ $$

Commented by floor(10²Eta[1]) last updated on 29/Aug/20

well... it′s true even you think that is not a ′′good argument′′

$$\mathrm{well}...\:\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{even}\:\mathrm{you}\:\mathrm{think} \\ $$$$\mathrm{that}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:''\mathrm{good}\:\mathrm{argument}'' \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

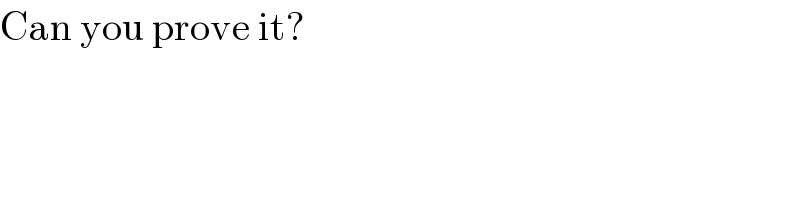
Can you prove it?

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{it}? \\ $$

Commented by floor(10²Eta[1]) last updated on 29/Aug/20

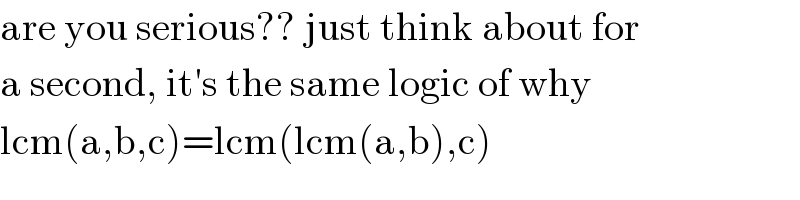
are you serious?? just think about for a second, it′s the same logic of why lcm(a,b,c)=lcm(lcm(a,b),c)

$$\mathrm{are}\:\mathrm{you}\:\mathrm{serious}??\:\mathrm{just}\:\mathrm{think}\:\mathrm{about}\:\mathrm{for}\: \\ $$$$\mathrm{a}\:\mathrm{second},\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{same}\:\mathrm{logic}\:\mathrm{of}\:\mathrm{why} \\ $$$$\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{c}\right) \\ $$

Commented by Aina Samuel Temidayo last updated on 30/Aug/20

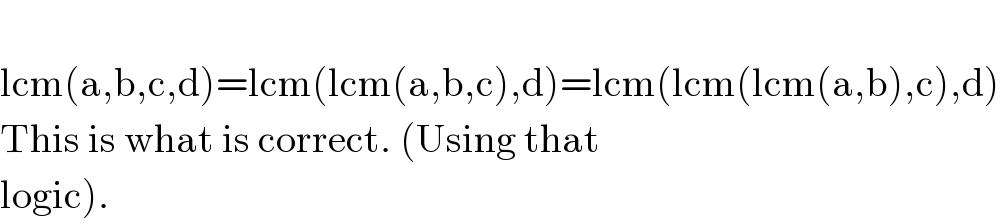
lcm(a,b,c,d)=lcm(lcm(a,b,c),d)=lcm(lcm(lcm(a,b),c),d) This is what is correct. (Using that logic).

$$ \\ $$$$\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b},\mathrm{c}\right),\mathrm{d}\right)=\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{lcm}\left(\mathrm{a},\mathrm{b}\right),\mathrm{c}\right),\mathrm{d}\right) \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{what}\:\mathrm{is}\:\mathrm{correct}.\:\left(\mathrm{Using}\:\mathrm{that}\right. \\ $$$$\left.\mathrm{logic}\right). \\ $$

Commented by floor(10²Eta[1]) last updated on 30/Aug/20

yeah this is also correct

$$\mathrm{yeah}\:\mathrm{this}\:\mathrm{is}\:\mathrm{also}\:\mathrm{correct}\: \\ $$

Commented by Aina Samuel Temidayo last updated on 30/Aug/20

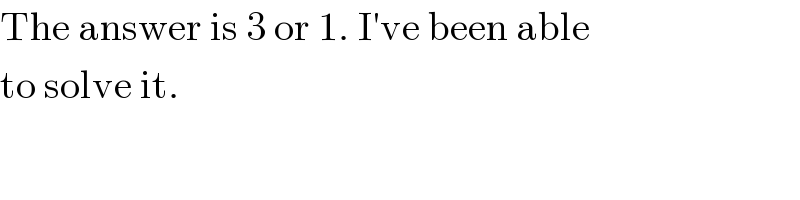
The answer is 3 or 1. I′ve been able to solve it.

$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{3}\:\mathrm{or}\:\mathrm{1}.\:\mathrm{I}'\mathrm{ve}\:\mathrm{been}\:\mathrm{able} \\ $$$$\mathrm{to}\:\mathrm{solve}\:\mathrm{it}. \\ $$

Commented by floor(10²Eta[1]) last updated on 30/Aug/20

congratulations

$$\mathrm{congratulations} \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 30/Aug/20

let lcm(a,b)=x ,lcm(c,d)=y⇒ lcm(a,b,c,d)=lcm(lcm(a,b,c),d)= lcm(lcm(lcm(a,b),c),d)=lcm(lcm(x,c),d)= lcm(x,c,d)=lcm(x,lcm(c,d))=lcm(x,y)

$${let}\:{lcm}\left({a},{b}\right)={x}\:,{lcm}\left({c},{d}\right)={y}\Rightarrow \\ $$$${lcm}\left({a},{b},{c},{d}\right)={lcm}\left({lcm}\left({a},{b},{c}\right),{d}\right)= \\ $$$${lcm}\left({lcm}\left({lcm}\left({a},{b}\right),{c}\right),{d}\right)={lcm}\left({lcm}\left({x},{c}\right),{d}\right)= \\ $$$${lcm}\left({x},{c},{d}\right)={lcm}\left({x},{lcm}\left({c},{d}\right)\right)={lcm}\left({x},{y}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com