Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 110591 by Aina Samuel Temidayo last updated on 29/Aug/20

Find the sum of all positive two−digit integers that are divisible by each of their digits.

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{positive} \\ $$$$\mathrm{two}−\mathrm{digit}\:\mathrm{integers}\:\mathrm{that}\:\mathrm{are}\:\mathrm{divisible} \\ $$$$\mathrm{by}\:\mathrm{each}\:\mathrm{of}\:\mathrm{their}\:\mathrm{digits}. \\ $$

Answered by Rasheed.Sindhi last updated on 30/Aug/20

Let N=10t+u is a number such that u ∣ 10t+u ∧ t ∣ 10t+u 10t+u=mu ∧ 10t+u=nt (N is common multiple of m & n) u=((10t)/(m−1)) ∧ u=t(n−10) ((10t)/(m−1))=t(n−10) t≠0(∵ The number is of 2-digit) ((10)/(m−1))=n−10 (m−1)(n−10)=10 m−1=a ∧ n−10=10/a [ Where a ∣ 10 ] ( m,n)=(a+1,10+((10)/a)) As N=common multiple of m & n or a+1 & 10+((10)/a). So, N=k lcm(a+1,10+((10)/a)) for some k (∈N) Four possible cases ^(★1) m−1=1 ∧ n−10=10 (m,n)=(2,20) N=k lcm(2,20) N=20^(×) ,40^(×) ,60^(×) ,80^(×) (No value of N) ^(★2) m−1=2 ∧ n−10=5 (m,n)=(3,15) N=klcm(3,15) N=15,30^(×) ,45^(×) ,60^(×) ,75^(×) ,90^(×) ^(★3) m−1=5 ∧ n−10=2 (m,n)=(6,12) N=klcm(12,6) N=12,24,36,48,60^(×) ,72^(×) ,84^(×) ,96^(×) ^(★4) m−1=10 ∧ n−10=1 (m,n)=(11,11) N=klcm(11,11) N=11,22,33,44,55,66,77,88,99 Red numbers are successful.

$${Let}\:{N}=\mathrm{10}{t}+{u}\:{is}\:{a}\:{number}\:{such} \\ $$$${that}\:{u}\:\mid\:\mathrm{10}{t}+{u}\:\wedge\:{t}\:\mid\:\mathrm{10}{t}+{u} \\ $$$$\:\:\:\:\:\:\mathrm{10}{t}+{u}={mu}\:\wedge\:\mathrm{10}{t}+{u}={nt} \\ $$$$\:\left({N}\:{is}\:{common}\:{multiple}\:{of}\:{m}\:\&\:{n}\right) \\ $$$$\:\:\:\:\:\:\:{u}=\frac{\mathrm{10}{t}}{{m}−\mathrm{1}}\:\wedge\:{u}={t}\left({n}−\mathrm{10}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{10}{t}}{{m}−\mathrm{1}}={t}\left({n}−\mathrm{10}\right) \\ $$$${t}\neq\mathrm{0}\left(\because\:{The}\:{number}\:{is}\:{of}\:\mathrm{2}-{digit}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{10}}{{m}−\mathrm{1}}={n}−\mathrm{10} \\ $$$$\:\:\:\left({m}−\mathrm{1}\right)\left({n}−\mathrm{10}\right)=\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\:{m}−\mathrm{1}={a}\:\wedge\:{n}−\mathrm{10}=\mathrm{10}/{a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\:{Where}\:{a}\:\mid\:\mathrm{10}\:\right] \\ $$$$\:\:\:\:\:\:\:\:\left(\:{m},{n}\right)=\left({a}+\mathrm{1},\mathrm{10}+\frac{\mathrm{10}}{{a}}\right) \\ $$$${As}\:{N}={common}\:{multiple}\:{of}\:{m}\:\&\:{n} \\ $$$${or}\:{a}+\mathrm{1}\:\&\:\mathrm{10}+\frac{\mathrm{10}}{{a}}.\: \\ $$$${So}, \\ $$$${N}={k}\:\mathrm{lcm}\left({a}+\mathrm{1},\mathrm{10}+\frac{\mathrm{10}}{{a}}\right)\:\mathrm{for}\:\mathrm{some}\:\mathrm{k} \\ $$$$\left(\in\mathbb{N}\right) \\ $$$${Four}\:{possible}\:{cases} \\ $$$$\:^{\bigstar\mathrm{1}} \:{m}−\mathrm{1}=\mathrm{1}\:\wedge\:{n}−\mathrm{10}=\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\left({m},{n}\right)=\left(\mathrm{2},\mathrm{20}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{N}={k}\:\mathrm{lcm}\left(\mathrm{2},\mathrm{20}\right) \\ $$$$\:\:\:\:\:{N}=\overset{×} {\mathrm{20}},\overset{×} {\mathrm{40}},\overset{×} {\mathrm{60}},\overset{×} {\mathrm{80}}\:\left({No}\:{value}\:{of}\:{N}\right) \\ $$$$\:^{\bigstar\mathrm{2}} {m}−\mathrm{1}=\mathrm{2}\:\wedge\:{n}−\mathrm{10}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\left({m},{n}\right)=\left(\mathrm{3},\mathrm{15}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{N}={k}\mathrm{lcm}\left(\mathrm{3},\mathrm{15}\right) \\ $$$$\:\:\:\:\:\:\:{N}=\mathrm{15},\overset{×} {\mathrm{30}},\overset{×} {\mathrm{45}},\overset{×} {\mathrm{60}},\overset{×} {\mathrm{75}},\overset{×} {\mathrm{90}} \\ $$$$\:^{\bigstar\mathrm{3}} {m}−\mathrm{1}=\mathrm{5}\:\wedge\:{n}−\mathrm{10}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({m},{n}\right)=\left(\mathrm{6},\mathrm{12}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{N}={klcm}\left(\mathrm{12},\mathrm{6}\right) \\ $$$$\:\:\:\:{N}=\mathrm{12},\mathrm{24},\mathrm{36},\mathrm{48},\overset{×} {\mathrm{60}},\overset{×} {\mathrm{72}},\overset{×} {\mathrm{84}},\overset{×} {\mathrm{96}} \\ $$$$\:^{\bigstar\mathrm{4}} {m}−\mathrm{1}=\mathrm{10}\:\wedge\:{n}−\mathrm{10}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left({m},{n}\right)=\left(\mathrm{11},\mathrm{11}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{N}={k}\mathrm{lcm}\left(\mathrm{11},\mathrm{11}\right) \\ $$$$\:\:\:{N}=\mathrm{11},\mathrm{22},\mathrm{33},\mathrm{44},\mathrm{55},\mathrm{66},\mathrm{77},\mathrm{88},\mathrm{99} \\ $$$$\:\:{Red}\:{numbers}\:{are}\:{successful}. \\ $$

Commented by Aina Samuel Temidayo last updated on 29/Aug/20

Thanks but please try to complete it. I post questions because I don′t really have any idea of how to solve them.

$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{please}\:\mathrm{try}\:\mathrm{to}\:\mathrm{complete}\:\mathrm{it}.\:\mathrm{I} \\ $$$$\mathrm{post}\:\mathrm{questions}\:\mathrm{because}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{really}\:\mathrm{have}\:\mathrm{any}\:\mathrm{idea} \\ $$$$\mathrm{of}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{them}. \\ $$

Commented by Rasheed.Sindhi last updated on 30/Aug/20

Completed the answer

$${Completed}\:{the}\:{answer} \\ $$

Answered by floor(10²Eta[1]) last updated on 29/Aug/20

first of all, we have 3 obvious things: (1):this works with all multiple of 11 (2):this doesn′t work with any prime number (except 11) (3):this doesn′t work with any multiple of 10 (because we can′t say that 0 divides something) 10a+b s.t. a∣10a+b∧b∣10a+b ⇒a∣b and b∣10a so or b∣10⇒b=1, 2 or 5 or b∣a⇒a=b (because a∣b) but when a=b is the 1 case that i said so let′s see when b=1, 2, 5 b=1⇒(11, 21, 31, 41, 51, 61, 71, 81, 91) works: (11) b=2⇒(12, 22, 32, 42, 52, 62, 72, 82, 92) works: (12, 22) b=5⇒(15, 25, 35, 45, 55, 65, 75, 85, 95) works: (15, 55) only cases that works: (12, 15, and all multiples of 11) so the sum of these numbers are 12+15+11(1+2+3+4+...+9) =27+11.45=522

$$\mathrm{first}\:\mathrm{of}\:\mathrm{all},\:\mathrm{we}\:\mathrm{have}\:\mathrm{3}\:\mathrm{obvious}\:\mathrm{things}: \\ $$$$\left(\mathrm{1}\right):\mathrm{this}\:\mathrm{works}\:\mathrm{with}\:\mathrm{all}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{11} \\ $$$$\left(\mathrm{2}\right):\mathrm{this}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}\:\mathrm{with}\:\mathrm{any}\:\mathrm{prime}\: \\ $$$$\mathrm{number}\:\left(\mathrm{except}\:\mathrm{11}\right) \\ $$$$\left(\mathrm{3}\right):\mathrm{this}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work}\:\mathrm{with}\:\mathrm{any}\:\mathrm{multiple} \\ $$$$\mathrm{of}\:\mathrm{10}\:\left(\mathrm{because}\:\mathrm{we}\:\mathrm{can}'\mathrm{t}\:\mathrm{say}\:\mathrm{that}\:\mathrm{0}\:\mathrm{divides}\right. \\ $$$$\left.\mathrm{something}\right) \\ $$$$ \\ $$$$\mathrm{10a}+\mathrm{b}\:\mathrm{s}.\mathrm{t}.\:\mathrm{a}\mid\mathrm{10a}+\mathrm{b}\wedge\mathrm{b}\mid\mathrm{10a}+\mathrm{b} \\ $$$$\Rightarrow\mathrm{a}\mid\mathrm{b}\:\mathrm{and}\:\mathrm{b}\mid\mathrm{10a} \\ $$$$\mathrm{so}\:\mathrm{or}\:\mathrm{b}\mid\mathrm{10}\Rightarrow\mathrm{b}=\mathrm{1},\:\mathrm{2}\:\mathrm{or}\:\mathrm{5} \\ $$$$\mathrm{or}\:\mathrm{b}\mid\mathrm{a}\Rightarrow\mathrm{a}=\mathrm{b}\:\left(\mathrm{because}\:\mathrm{a}\mid\mathrm{b}\right) \\ $$$$\mathrm{but}\:\mathrm{when}\:\mathrm{a}=\mathrm{b}\:\mathrm{is}\:\mathrm{the}\:\mathrm{1}\:\mathrm{case}\:\mathrm{that}\:\mathrm{i}\:\mathrm{said} \\ $$$$\mathrm{so}\:\mathrm{let}'\mathrm{s}\:\mathrm{see}\:\mathrm{when}\:\mathrm{b}=\mathrm{1},\:\mathrm{2},\:\mathrm{5} \\ $$$$\mathrm{b}=\mathrm{1}\Rightarrow\left(\mathrm{11},\:\mathrm{21},\:\mathrm{31},\:\mathrm{41},\:\mathrm{51},\:\mathrm{61},\:\mathrm{71},\:\mathrm{81},\:\mathrm{91}\right) \\ $$$$\mathrm{works}:\:\left(\mathrm{11}\right) \\ $$$$\mathrm{b}=\mathrm{2}\Rightarrow\left(\mathrm{12},\:\mathrm{22},\:\mathrm{32},\:\mathrm{42},\:\mathrm{52},\:\mathrm{62},\:\mathrm{72},\:\mathrm{82},\:\mathrm{92}\right) \\ $$$$\mathrm{works}:\:\left(\mathrm{12},\:\mathrm{22}\right) \\ $$$$\mathrm{b}=\mathrm{5}\Rightarrow\left(\mathrm{15},\:\mathrm{25},\:\mathrm{35},\:\mathrm{45},\:\mathrm{55},\:\mathrm{65},\:\mathrm{75},\:\mathrm{85},\:\mathrm{95}\right) \\ $$$$\mathrm{works}:\:\left(\mathrm{15},\:\mathrm{55}\right) \\ $$$$\mathrm{only}\:\mathrm{cases}\:\mathrm{that}\:\mathrm{works}: \\ $$$$\left(\mathrm{12},\:\mathrm{15},\:\mathrm{and}\:\mathrm{all}\:\mathrm{multiples}\:\mathrm{of}\:\mathrm{11}\right) \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{these}\:\mathrm{numbers}\:\mathrm{are} \\ $$$$\mathrm{12}+\mathrm{15}+\mathrm{11}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+\mathrm{9}\right) \\ $$$$=\mathrm{27}+\mathrm{11}.\mathrm{45}=\mathrm{522} \\ $$

Commented by Aina Samuel Temidayo last updated on 30/Aug/20

Thanks but I don′t think this is correct.

$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is} \\ $$$$\mathrm{correct}. \\ $$

Commented by floor(10²Eta[1]) last updated on 30/Aug/20

?????why

$$?????\mathrm{why} \\ $$

Answered by mr W last updated on 30/Aug/20

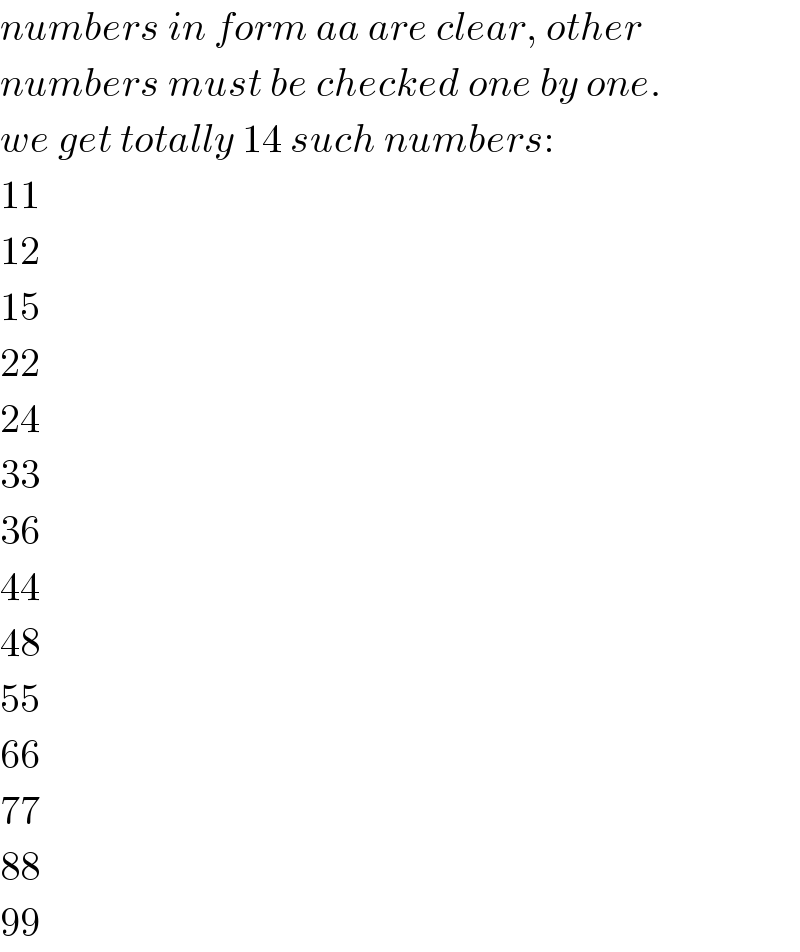
numbers in form aa are clear, other numbers must be checked one by one. we get totally 14 such numbers: 11 12 15 22 24 33 36 44 48 55 66 77 88 99

$${numbers}\:{in}\:{form}\:{aa}\:{are}\:{clear},\:{other} \\ $$$${numbers}\:{must}\:{be}\:{checked}\:{one}\:{by}\:{one}. \\ $$$${we}\:{get}\:{totally}\:\mathrm{14}\:{such}\:{numbers}: \\ $$$$\mathrm{11} \\ $$$$\mathrm{12} \\ $$$$\mathrm{15} \\ $$$$\mathrm{22} \\ $$$$\mathrm{24} \\ $$$$\mathrm{33} \\ $$$$\mathrm{36} \\ $$$$\mathrm{44} \\ $$$$\mathrm{48} \\ $$$$\mathrm{55} \\ $$$$\mathrm{66} \\ $$$$\mathrm{77} \\ $$$$\mathrm{88} \\ $$$$\mathrm{99} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com