
Question Number 110704 by Aina Samuel Temidayo last updated on 30/Aug/20
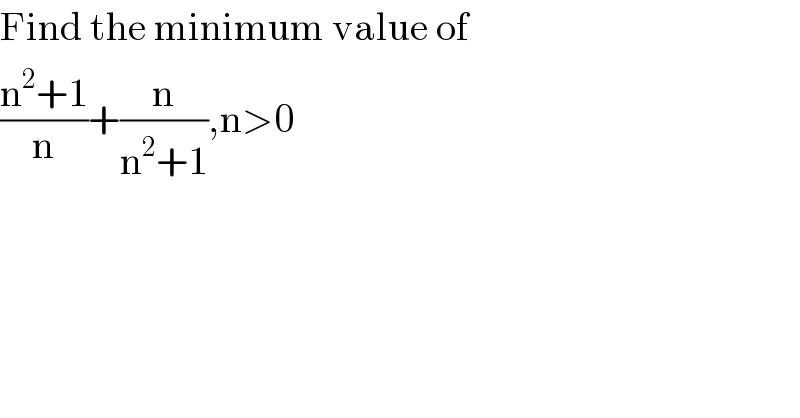
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$ $$\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}},\mathrm{n}>\mathrm{0} \\ $$
Answered by mr W last updated on 30/Aug/20

$$\frac{{n}^{\mathrm{2}} +\mathrm{1}}{{n}}+\frac{{n}}{{n}^{\mathrm{2}} +\mathrm{1}} \\ $$ $$=\left({n}+\frac{\mathrm{1}}{{n}}\right)+\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{{n}}\right)} \\ $$ $${n}+\frac{\mathrm{1}}{{n}}\geqslant\mathrm{2}\sqrt{{n}×\frac{\mathrm{1}}{{n}}}=\mathrm{2} \\ $$ $${so}\:{the}\:{question}\:{is}\:{to}\:{find}\:{the}\:{minimum} \\ $$ $${of}\:{function}\:{f}\left({x}\right)={x}+\frac{\mathrm{1}}{{x}}\:{for}\:{x}\geqslant\mathrm{2}. \\ $$ $${f}'\left({x}\right)=\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }>\mathrm{0}\:{for}\:{x}>\mathrm{1} \\ $$ $${that}\:{means}\:{f}\left({x}\right)\:{is}\:{strictly}\:{increasing} \\ $$ $${for}\:{x}>\mathrm{1},\:{so}\:{for}\:{x}\geqslant\mathrm{2}\:{we}\:{have} \\ $$ $${f}\left({x}\right)_{{min}} ={f}\left(\mathrm{2}\right)=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}}. \\ $$
Answered by floor(10²Eta[1]) last updated on 30/Aug/20
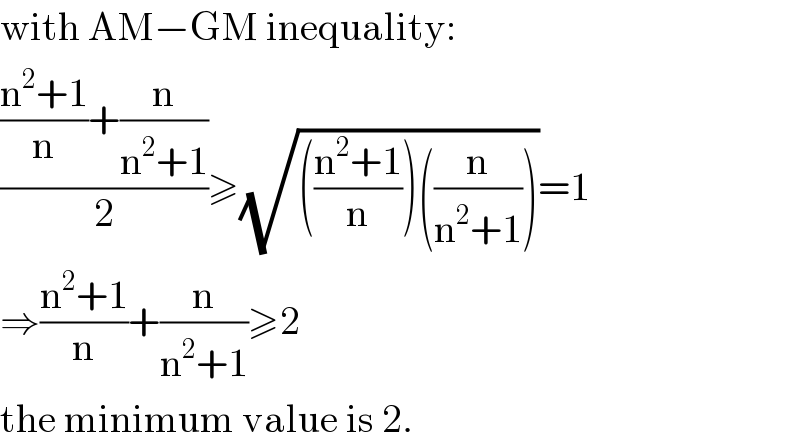
$$\mathrm{with}\:\mathrm{AM}−\mathrm{GM}\:\mathrm{inequality}: \\ $$ $$\frac{\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}}\geqslant\sqrt{\left(\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}}\right)\left(\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}\right)}=\mathrm{1} \\ $$ $$\Rightarrow\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}\geqslant\mathrm{2} \\ $$ $$\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{is}\:\mathrm{2}. \\ $$
Commented byAina Samuel Temidayo last updated on 30/Aug/20
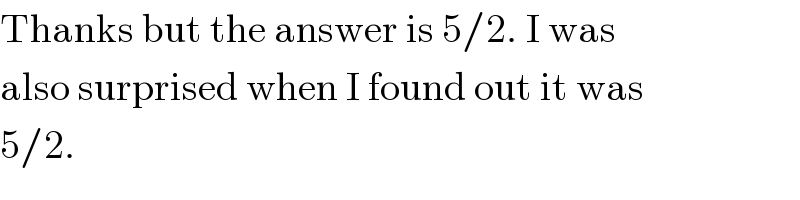
$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{5}/\mathrm{2}.\:\mathrm{I}\:\mathrm{was} \\ $$ $$\mathrm{also}\:\mathrm{surprised}\:\mathrm{when}\:\mathrm{I}\:\mathrm{found}\:\mathrm{out}\:\mathrm{it}\:\mathrm{was} \\ $$ $$\mathrm{5}/\mathrm{2}. \\ $$
Commented byAina Samuel Temidayo last updated on 30/Aug/20
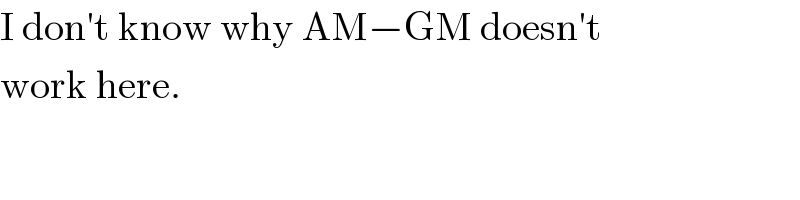
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{why}\:\mathrm{AM}−\mathrm{GM}\:\mathrm{doesn}'\mathrm{t} \\ $$ $$\mathrm{work}\:\mathrm{here}. \\ $$
Commented bymnjuly1970 last updated on 30/Aug/20
![if (min =2) then : ((n^2 +1)/n) =(n/(n^2 +1))⇒n^4 +2n^2 +1=n^2 n^4 +n^2 +1=0⇒n∉R solution: F(n)=(n+^([min]]) (1/n)) +((1^([max]) /(n +(1/n)))) min(F(n))=2+(1/2) =(5/2) ...M.N.july 1970#](Q110718.png)
$${if}\:\left({min}\:=\mathrm{2}\right)\:{then}\:: \\ $$ $$ \\ $$ $$\frac{{n}^{\mathrm{2}} +\mathrm{1}}{{n}}\:=\frac{{n}}{{n}^{\mathrm{2}} +\mathrm{1}}\Rightarrow{n}^{\mathrm{4}} +\mathrm{2}{n}^{\mathrm{2}} +\mathrm{1}={n}^{\mathrm{2}} \\ $$ $${n}^{\mathrm{4}} +{n}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\Rightarrow{n}\notin\mathbb{R} \\ $$ $$ \\ $$ $${solution}:\:\mathrm{F}\left({n}\right)=\left({n}\overset{\left.\left[{min}\right]\right]} {+}\frac{\mathrm{1}}{{n}}\right)\:+\left(\frac{\overset{\left[{max}\right]} {\mathrm{1}}}{{n}\:+\frac{\mathrm{1}}{{n}}}\right)\:\:\:\:\: \\ $$ $$\:\:\:\:\:\:\:\:\:\:{min}\left(\mathrm{F}\left({n}\right)\right)=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{5}}{\mathrm{2}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:...\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}# \\ $$
Commented byAina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{Thanks}. \\ $$
Answered by $@y@m last updated on 30/Aug/20
![Let y=((n^2 +1)/n)+(n/(n^2 +1)),n>0 ⇒y=(((n^2 +1)^2 +n^2 )/(n(n^2 +1))) ⇒y=((n^4 +3n^2 +1)/(n^3 +n)) (dy/dn)=(((n^3 +n)(4n^3 +6n)−(n^4 +3n^2 +1)(3n^2 +1))/((n^3 +n)^2 )) (dy/dn)=((4n^6 +10n^4 +6n^2 −(3n^6 +10n^4 +6n^2 +1))/((n^3 +n)^2 )) (dy/dn)=((n^6 −1)/((n^3 +n)^2 )) ....(1) For maxima or minima, (dy/dn)=0 ⇒n^6 −1=0 ⇒n=1 Now, (d^2 y/dn^2 )=(((n^3 +n)^2 6n^5 −(n^6 −1).2(n^3 +n)(3n^2 +1))/((n^3 +n)^4 )) [(d^2 y/dn_( ) ^2 )]_(at n=1) =((4.6.1−0)/2^4 )=(3/2)>0 ∴ y is minimum at n=1 ⇒y_(min) =((1^2 +1)/1)+(1/(1^2 +1))=2+(1/2)=(5/2)](Q110732.png)
$${Let}\:{y}=\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}},\mathrm{n}>\mathrm{0} \\ $$ $$\Rightarrow{y}=\frac{\left({n}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} }{{n}\left({n}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$ $$\Rightarrow{y}=\frac{{n}^{\mathrm{4}} +\mathrm{3}{n}^{\mathrm{2}} +\mathrm{1}}{{n}^{\mathrm{3}} +{n}} \\ $$ $$\frac{{dy}}{{dn}}=\frac{\left({n}^{\mathrm{3}} +{n}\right)\left(\mathrm{4}{n}^{\mathrm{3}} +\mathrm{6}{n}\right)−\left({n}^{\mathrm{4}} +\mathrm{3}{n}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{1}\right)}{\left({n}^{\mathrm{3}} +{n}\right)^{\mathrm{2}} } \\ $$ $$\frac{{dy}}{{dn}}=\frac{\mathrm{4}{n}^{\mathrm{6}} +\mathrm{10}{n}^{\mathrm{4}} +\mathrm{6}{n}^{\mathrm{2}} −\left(\mathrm{3}{n}^{\mathrm{6}} +\mathrm{10}{n}^{\mathrm{4}} +\mathrm{6}{n}^{\mathrm{2}} +\mathrm{1}\right)}{\left({n}^{\mathrm{3}} +{n}\right)^{\mathrm{2}} } \\ $$ $$\frac{{dy}}{{dn}}=\frac{{n}^{\mathrm{6}} −\mathrm{1}}{\left({n}^{\mathrm{3}} +{n}\right)^{\mathrm{2}} }\:\:\:....\left(\mathrm{1}\right) \\ $$ $${For}\:{maxima}\:{or}\:{minima}, \\ $$ $$\frac{{dy}}{{dn}}=\mathrm{0} \\ $$ $$\Rightarrow{n}^{\mathrm{6}} −\mathrm{1}=\mathrm{0} \\ $$ $$\Rightarrow{n}=\mathrm{1} \\ $$ $${Now},\:\frac{{d}^{\mathrm{2}} {y}}{{dn}^{\mathrm{2}} }=\frac{\left({n}^{\mathrm{3}} +{n}\right)^{\mathrm{2}} \mathrm{6}{n}^{\mathrm{5}} −\left({n}^{\mathrm{6}} −\mathrm{1}\right).\mathrm{2}\left({n}^{\mathrm{3}} +{n}\right)\left(\mathrm{3}{n}^{\mathrm{2}} +\mathrm{1}\right)}{\left({n}^{\mathrm{3}} +{n}\right)^{\mathrm{4}} } \\ $$ $$\:\left[\frac{{d}^{\mathrm{2}} {y}}{{dn}_{\:\:} ^{\mathrm{2}} }\right]_{{at}\:{n}=\mathrm{1}} =\frac{\mathrm{4}.\mathrm{6}.\mathrm{1}−\mathrm{0}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{3}}{\mathrm{2}}>\mathrm{0} \\ $$ $$\therefore\:{y}\:{is}\:{minimum}\:{at}\:{n}=\mathrm{1} \\ $$ $$\Rightarrow{y}_{{min}} =\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$ $$ \\ $$
Commented byAina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Thanks}. \\ $$
