Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 11075 by Joel576 last updated on 10/Mar/17

Let n be the smallest positive integer that is a multiple of 75 and has exactly 75 positive integral divisors, including 1 and itself. Find (n/(75))

$$\mathrm{Let}\:{n}\:\mathrm{be}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{that}\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{75}\:\mathrm{and}\:\mathrm{has}\:\mathrm{exactly}\:\mathrm{75}\:\mathrm{positive} \\ $$$$\mathrm{integral}\:\mathrm{divisors},\:\mathrm{including}\:\mathrm{1}\:\mathrm{and}\:\mathrm{itself}. \\ $$$$\mathrm{Find}\:\frac{{n}}{\mathrm{75}} \\ $$

Commented by FilupS last updated on 11/Mar/17

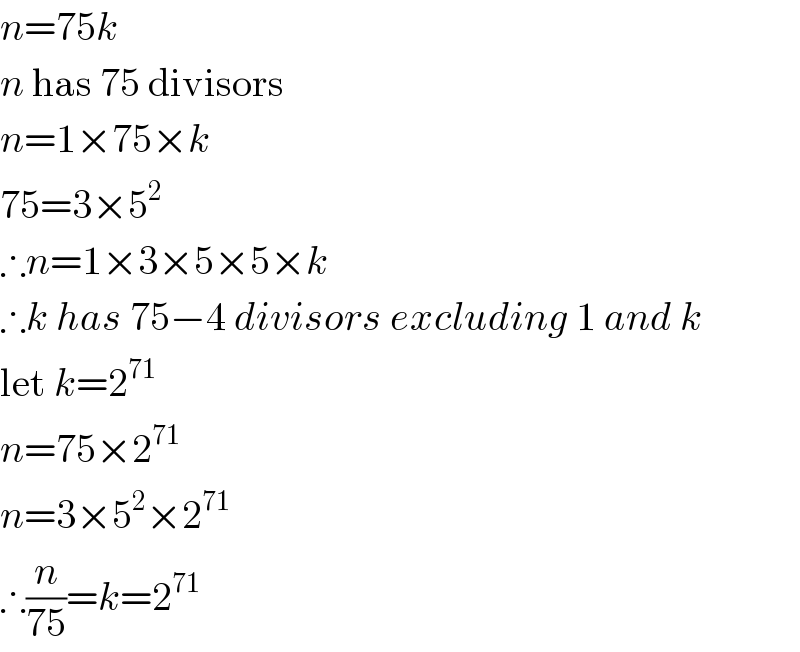
n=75k n has 75 divisors n=1×75×k 75=3×5^2 ∴n=1×3×5×5×k ∴k has 75−4 divisors excluding 1 and k let k=2^(71) n=75×2^(71) n=3×5^2 ×2^(71) ∴(n/(75))=k=2^(71)

$${n}=\mathrm{75}{k} \\ $$$${n}\:\mathrm{has}\:\mathrm{75}\:\mathrm{divisors} \\ $$$${n}=\mathrm{1}×\mathrm{75}×{k} \\ $$$$\mathrm{75}=\mathrm{3}×\mathrm{5}^{\mathrm{2}} \\ $$$$\therefore{n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×{k} \\ $$$$\therefore{k}\:{has}\:\mathrm{75}−\mathrm{4}\:{divisors}\:{excluding}\:\mathrm{1}\:{and}\:{k} \\ $$$$\mathrm{let}\:{k}=\mathrm{2}^{\mathrm{71}} \\ $$$${n}=\mathrm{75}×\mathrm{2}^{\mathrm{71}} \\ $$$${n}=\mathrm{3}×\mathrm{5}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{71}} \\ $$$$\therefore\frac{{n}}{\mathrm{75}}={k}=\mathrm{2}^{\mathrm{71}} \\ $$

Commented by mrW1 last updated on 14/Mar/17

The answer to this question depents very much on how to understand the condition “it has exactly 75 divisors”. Let′s look at an easier case that it has exactly 5 divisors. According to your consideration above the answer should be n=1×3×5×5×2^1 =150 But this number has not exactly only 5 divisors, but much more. All following numbers are divisors of it: 1/3/5/2 15/6 25/10 75/30/50 150 −−−−− that means the number n=150 has in fact not exactly 5 divisors, but exactly 12 different divisors. An orther problem is if identical divisors are allowed or not. Since 1 is definitely allowed, according to your consideration the answer should be n=1×3×5×5×1^(71) =75

$${The}\:{answer}\:{to}\:{this}\:{question}\:{depents} \\ $$$${very}\:{much}\:{on}\:{how}\:{to}\:{understand}\:{the} \\ $$$${condition}\:``{it}\:{has}\:{exactly}\:\mathrm{75}\:{divisors}''. \\ $$$$ \\ $$$${Let}'{s}\:{look}\:{at}\:{an}\:{easier}\:{case}\:{that}\:{it}\:{has} \\ $$$${exactly}\:\mathrm{5}\:{divisors}.\:{According}\:{to}\:{your} \\ $$$${consideration}\:{above}\:{the}\:{answer}\:{should} \\ $$$${be} \\ $$$${n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{2}^{\mathrm{1}} =\mathrm{150} \\ $$$${But}\:{this}\:{number}\:{has}\:{not}\:{exactly}\:{only} \\ $$$$\mathrm{5}\:{divisors},\:{but}\:{much}\:{more}.\:{All}\:{following} \\ $$$${numbers}\:{are}\:{divisors}\:{of}\:{it}: \\ $$$$\mathrm{1}/\mathrm{3}/\mathrm{5}/\mathrm{2} \\ $$$$\mathrm{15}/\mathrm{6} \\ $$$$\mathrm{25}/\mathrm{10} \\ $$$$\mathrm{75}/\mathrm{30}/\mathrm{50} \\ $$$$\mathrm{150} \\ $$$$−−−−− \\ $$$${that}\:{means}\:{the}\:{number}\:{n}=\mathrm{150}\:{has} \\ $$$${in}\:{fact}\:{not}\:{exactly}\:\mathrm{5}\:{divisors},\:{but} \\ $$$${exactly}\:\mathrm{12}\:{different}\:{divisors}. \\ $$$$ \\ $$$${An}\:{orther}\:{problem}\:{is}\:{if}\:{identical}\:{divisors} \\ $$$${are}\:{allowed}\:{or}\:{not}.\:{Since}\:\mathrm{1}\:{is}\:{definitely} \\ $$$${allowed},\:{according}\:{to}\:{your}\:{consideration} \\ $$$${the}\:{answer}\:{should}\:{be} \\ $$$${n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{1}^{\mathrm{71}} =\mathrm{75} \\ $$

Commented by FilupS last updated on 11/Mar/17

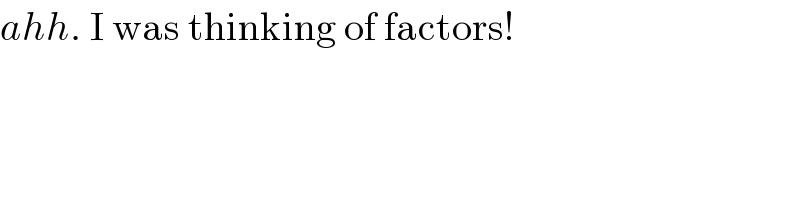
ahh. I was thinking of factors!

$${ahh}.\:\mathrm{I}\:\mathrm{was}\:\mathrm{thinking}\:\mathrm{of}\:\mathrm{factors}! \\ $$

Commented by mrW1 last updated on 11/Mar/17

I made following consideration: n=p_1 ×p_2 ×p_3 ....×p_m =Π_(k=1) ^m p_k p_k =the k−th prime number. n has following kinds of divisors: − each of the m prime numbers: C_1 ^m =((m!)/(1!(m−1)!))=m − product of every 2 of the m prime numbers: C_2 ^m =((m!)/(2!(m−2)!)) − product of every 3 of the m prime numbers: C_3 ^m =((m!)/(3!(m−3)!)) ...... − product of all of the m prime numbers: C_m ^m =((m!)/(m!(m−m)!))=1 that means the total number of divisors is Σ_(k=1) ^m C_k ^m =Σ_(k=1) ^m ((m!)/(k!(m−k)!))=2^m −1

$${I}\:{made}\:{following}\:{consideration}: \\ $$$${n}={p}_{\mathrm{1}} ×{p}_{\mathrm{2}} ×{p}_{\mathrm{3}} ....×{p}_{{m}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}{p}_{{k}} \\ $$$${p}_{{k}} ={the}\:{k}−{th}\:{prime}\:{number}. \\ $$$${n}\:{has}\:{following}\:{kinds}\:{of}\:{divisors}: \\ $$$$−\:{each}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{\mathrm{1}} ^{{m}} =\frac{{m}!}{\mathrm{1}!\left({m}−\mathrm{1}\right)!}={m} \\ $$$$−\:{product}\:{of}\:{every}\:\mathrm{2}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{\mathrm{2}} ^{{m}} \:=\frac{{m}!}{\mathrm{2}!\left({m}−\mathrm{2}\right)!} \\ $$$$−\:{product}\:{of}\:{every}\:\mathrm{3}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{\mathrm{3}} ^{{m}} \:=\frac{{m}!}{\mathrm{3}!\left({m}−\mathrm{3}\right)!} \\ $$$$...... \\ $$$$−\:{product}\:{of}\:{all}\:{of}\:{the}\:{m}\:{prime}\:{numbers}:\:{C}_{{m}} ^{{m}} \:=\frac{{m}!}{{m}!\left({m}−{m}\right)!}=\mathrm{1} \\ $$$$ \\ $$$${that}\:{means}\:{the}\:{total}\:{number}\:{of}\:{divisors}\:{is} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{C}_{{k}} ^{{m}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{m}!}{{k}!\left({m}−{k}\right)!}=\mathrm{2}^{{m}} −\mathrm{1} \\ $$

Commented by FilupS last updated on 12/Mar/17

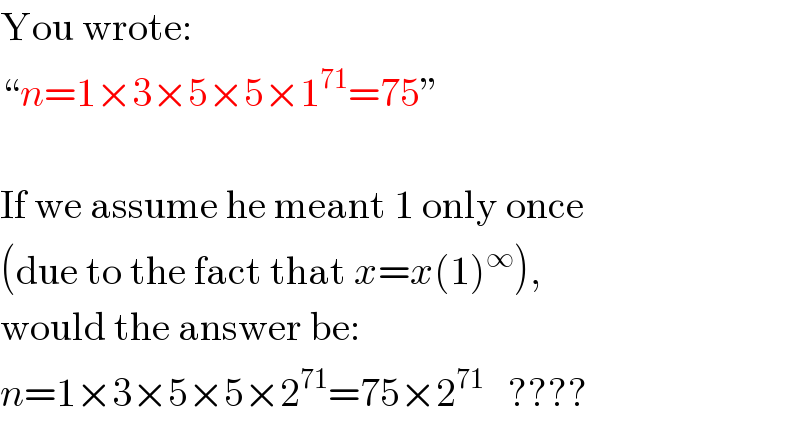
You wrote: “n=1×3×5×5×1^(71) =75” If we assume he meant 1 only once (due to the fact that x=x(1)^∞ ), would the answer be: n=1×3×5×5×2^(71) =75×2^(71) ????

$$\mathrm{You}\:\mathrm{wrote}: \\ $$$$``{n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{1}^{\mathrm{71}} =\mathrm{75}'' \\ $$$$\: \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{assume}\:\mathrm{he}\:\mathrm{meant}\:\mathrm{1}\:\mathrm{only}\:\mathrm{once} \\ $$$$\left(\mathrm{due}\:\mathrm{to}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{that}\:{x}={x}\left(\mathrm{1}\right)^{\infty} \right), \\ $$$$\mathrm{would}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{be}: \\ $$$${n}=\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{5}×\mathrm{2}^{\mathrm{71}} =\mathrm{75}×\mathrm{2}^{\mathrm{71}} \:\:\:???? \\ $$

Commented by mrW1 last updated on 12/Mar/17

The difficulty lies on how to make the number to have exactly 75 divisors: − to get more divisors we should take more different prime numbers − to keep the number small we should use more 2′s. The general formula is n=2^n_1 ×3^n_2 ×5^n_3 ×7^n_4 ×11^n_5 ... with n_1 ,n_4 ,n_5 ,...≥0, n_2 ≥1,n_3 ≥2 The question is to determine n_1 ,n_2 ,n_3 ,... to keep n as small as possible and to have exactly 75 divisors. For example: n=2^(11) ×3×5^2 =153600 has 72 divisors n=2^(12) ×3×5^2 =307200 has 78 divisors n=2^3 ×3^2 ×5^2 ×7=12600 has 72 divisors n=2^4 ×3^2 ×5^2 ×7=25200 has 90 divisors n=2^2 ×3×5^2 ×7×11=23100 has 72 divisors n=2^3 ×3×5^2 ×7×11=46200 has 96 divisors We see it′s not the right way to use only factors 2. E.g. 2^(11) ×3×5^2 is much bigger than 2^3 ×3^2 ×5^2 ×7, but both have 72 divisors.

$${The}\:{difficulty}\:{lies}\:{on}\:{how}\:{to}\:{make} \\ $$$${the}\:{number}\:{to}\:{have}\:{exactly}\:\mathrm{75}\:{divisors}: \\ $$$$−\:{to}\:{get}\:{more}\:{divisors}\:{we}\:{should}\:{take} \\ $$$${more}\:{different}\:{prime}\:{numbers}\: \\ $$$$−\:{to}\:{keep}\:{the}\:{number}\:{small}\:{we}\:{should} \\ $$$${use}\:{more}\:\mathrm{2}'{s}. \\ $$$$ \\ $$$${The}\:{general}\:{formula}\:{is} \\ $$$${n}=\mathrm{2}^{{n}_{\mathrm{1}} } ×\mathrm{3}^{{n}_{\mathrm{2}} } ×\mathrm{5}^{{n}_{\mathrm{3}} } ×\mathrm{7}^{{n}_{\mathrm{4}} } ×\mathrm{11}^{{n}_{\mathrm{5}} } ... \\ $$$${with}\:{n}_{\mathrm{1}} ,{n}_{\mathrm{4}} ,{n}_{\mathrm{5}} ,...\geqslant\mathrm{0},\:{n}_{\mathrm{2}} \geqslant\mathrm{1},{n}_{\mathrm{3}} \geqslant\mathrm{2} \\ $$$$ \\ $$$${The}\:{question}\:{is}\:{to}\:{determine} \\ $$$${n}_{\mathrm{1}} ,{n}_{\mathrm{2}} ,{n}_{\mathrm{3}} ,... \\ $$$${to}\:{keep}\:{n}\:{as}\:{small}\:{as}\:{possible}\:{and} \\ $$$${to}\:{have}\:{exactly}\:\mathrm{75}\:{divisors}. \\ $$$$ \\ $$$${For}\:{example}: \\ $$$${n}=\mathrm{2}^{\mathrm{11}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} =\mathrm{153600}\:{has}\:\mathrm{72}\:{divisors} \\ $$$${n}=\mathrm{2}^{\mathrm{12}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} =\mathrm{307200}\:{has}\:\mathrm{78}\:{divisors} \\ $$$$ \\ $$$${n}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}=\mathrm{12600}\:{has}\:\mathrm{72}\:{divisors} \\ $$$${n}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}=\mathrm{25200}\:{has}\:\mathrm{90}\:{divisors} \\ $$$$ \\ $$$${n}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}×\mathrm{11}=\mathrm{23100}\:{has}\:\mathrm{72}\:{divisors} \\ $$$${n}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} ×\mathrm{7}×\mathrm{11}=\mathrm{46200}\:{has}\:\mathrm{96}\:{divisors} \\ $$$$ \\ $$$${We}\:{see}\:{it}'{s}\:{not}\:{the}\:{right}\:{way}\:{to}\:{use} \\ $$$${only}\:{factors}\:\mathrm{2}.\:{E}.{g}.\:\mathrm{2}^{\mathrm{11}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} \:{is}\:{much} \\ $$$${bigger}\:{than}\:\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{2}} ×\mathrm{7},\:{but}\:{both} \\ $$$${have}\:\mathrm{72}\:{divisors}. \\ $$

Answered by mrW1 last updated on 16/Mar/17

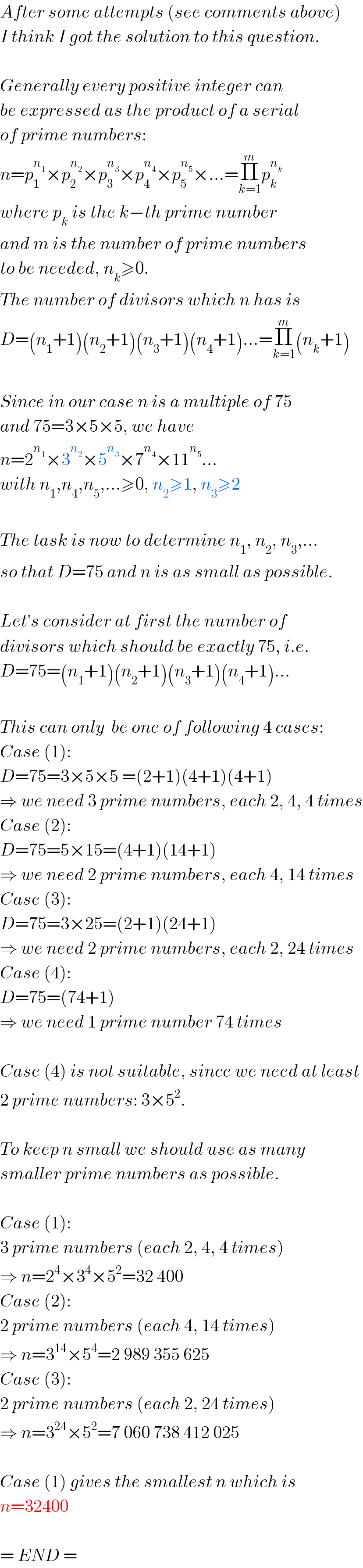
After some attempts (see comments above) I think I got the solution to this question. Generally every positive integer can be expressed as the product of a serial of prime numbers: n=p_1 ^n_1 ×p_2 ^n_2 ×p_3 ^n_3 ×p_4 ^n_4 ×p_5 ^n_5 ×...=Π_(k=1) ^m p_k ^n_k where p_k is the k−th prime number and m is the number of prime numbers to be needed, n_k ≥0. The number of divisors which n has is D=(n_1 +1)(n_2 +1)(n_3 +1)(n_4 +1)...=Π_(k=1) ^m (n_k +1) Since in our case n is a multiple of 75 and 75=3×5×5, we have n=2^n_1 ×3^n_2 ×5^n_3 ×7^n_4 ×11^n_5 ... with n_1 ,n_4 ,n_5 ,...≥0, n_2 ≥1, n_3 ≥2 The task is now to determine n_1 , n_2 , n_3 ,... so that D=75 and n is as small as possible. Let′s consider at first the number of divisors which should be exactly 75, i.e. D=75=(n_1 +1)(n_2 +1)(n_3 +1)(n_4 +1)... This can only be one of following 4 cases: Case (1): D=75=3×5×5 =(2+1)(4+1)(4+1) ⇒ we need 3 prime numbers, each 2, 4, 4 times Case (2): D=75=5×15=(4+1)(14+1) ⇒ we need 2 prime numbers, each 4, 14 times Case (3): D=75=3×25=(2+1)(24+1) ⇒ we need 2 prime numbers, each 2, 24 times Case (4): D=75=(74+1) ⇒ we need 1 prime number 74 times Case (4) is not suitable, since we need at least 2 prime numbers: 3×5^2 . To keep n small we should use as many smaller prime numbers as possible. Case (1): 3 prime numbers (each 2, 4, 4 times) ⇒ n=2^4 ×3^4 ×5^2 =32 400 Case (2): 2 prime numbers (each 4, 14 times) ⇒ n=3^(14) ×5^4 =2 989 355 625 Case (3): 2 prime numbers (each 2, 24 times) ⇒ n=3^(24) ×5^2 =7 060 738 412 025 Case (1) gives the smallest n which is n=32400 = END =

$${After}\:{some}\:{attempts}\:\left({see}\:{comments}\:{above}\right) \\ $$$${I}\:{think}\:{I}\:{got}\:{the}\:{solution}\:{to}\:{this}\:{question}. \\ $$$$ \\ $$$${Generally}\:{every}\:{positive}\:{integer}\:{can} \\ $$$${be}\:{expressed}\:{as}\:{the}\:{product}\:{of}\:{a}\:{serial} \\ $$$${of}\:{prime}\:{numbers}: \\ $$$${n}={p}_{\mathrm{1}} ^{{n}_{\mathrm{1}} } ×{p}_{\mathrm{2}} ^{{n}_{\mathrm{2}} } ×{p}_{\mathrm{3}} ^{{n}_{\mathrm{3}} } ×{p}_{\mathrm{4}} ^{{n}_{\mathrm{4}} } ×{p}_{\mathrm{5}} ^{{n}_{\mathrm{5}} } ×...=\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}{p}_{{k}} ^{{n}_{{k}} } \\ $$$${where}\:{p}_{{k}} \:{is}\:{the}\:{k}−{th}\:{prime}\:{number} \\ $$$${and}\:{m}\:{is}\:{the}\:{number}\:{of}\:{prime}\:{numbers} \\ $$$${to}\:{be}\:{needed},\:{n}_{{k}} \geqslant\mathrm{0}. \\ $$$${The}\:{number}\:{of}\:{divisors}\:{which}\:{n}\:{has}\:{is} \\ $$$${D}=\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)\left({n}_{\mathrm{3}} +\mathrm{1}\right)\left({n}_{\mathrm{4}} +\mathrm{1}\right)...=\underset{{k}=\mathrm{1}} {\overset{{m}} {\prod}}\left({n}_{{k}} +\mathrm{1}\right) \\ $$$$ \\ $$$${Since}\:{in}\:{our}\:{case}\:{n}\:{is}\:{a}\:{multiple}\:{of}\:\mathrm{75} \\ $$$${and}\:\mathrm{75}=\mathrm{3}×\mathrm{5}×\mathrm{5},\:{we}\:{have}\: \\ $$$${n}=\mathrm{2}^{{n}_{\mathrm{1}} } ×\mathrm{3}^{{n}_{\mathrm{2}} } ×\mathrm{5}^{{n}_{\mathrm{3}} } ×\mathrm{7}^{{n}_{\mathrm{4}} } ×\mathrm{11}^{{n}_{\mathrm{5}} } ... \\ $$$${with}\:{n}_{\mathrm{1}} ,{n}_{\mathrm{4}} ,{n}_{\mathrm{5}} ,...\geqslant\mathrm{0},\:{n}_{\mathrm{2}} \geqslant\mathrm{1},\:{n}_{\mathrm{3}} \geqslant\mathrm{2} \\ $$$$ \\ $$$${The}\:{task}\:{is}\:{now}\:{to}\:{determine}\:{n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} ,\:{n}_{\mathrm{3}} ,... \\ $$$${so}\:{that}\:{D}=\mathrm{75}\:{and}\:{n}\:{is}\:{as}\:{small}\:{as}\:{possible}. \\ $$$$ \\ $$$${Let}'{s}\:{consider}\:{at}\:{first}\:{the}\:{number}\:{of} \\ $$$${divisors}\:{which}\:{should}\:{be}\:{exactly}\:\mathrm{75},\:{i}.{e}. \\ $$$${D}=\mathrm{75}=\left({n}_{\mathrm{1}} +\mathrm{1}\right)\left({n}_{\mathrm{2}} +\mathrm{1}\right)\left({n}_{\mathrm{3}} +\mathrm{1}\right)\left({n}_{\mathrm{4}} +\mathrm{1}\right)... \\ $$$$ \\ $$$${This}\:{can}\:{only}\:\:{be}\:{one}\:{of}\:{following}\:\mathrm{4}\:{cases}: \\ $$$${Case}\:\left(\mathrm{1}\right): \\ $$$${D}=\mathrm{75}=\mathrm{3}×\mathrm{5}×\mathrm{5}\:=\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{4}+\mathrm{1}\right) \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{3}\:{prime}\:{numbers},\:{each}\:\mathrm{2},\:\mathrm{4},\:\mathrm{4}\:{times} \\ $$$${Case}\:\left(\mathrm{2}\right): \\ $$$${D}=\mathrm{75}=\mathrm{5}×\mathrm{15}=\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{14}+\mathrm{1}\right)\: \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{2}\:{prime}\:{numbers},\:{each}\:\mathrm{4},\:\mathrm{14}\:{times} \\ $$$${Case}\:\left(\mathrm{3}\right): \\ $$$${D}=\mathrm{75}=\mathrm{3}×\mathrm{25}=\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{24}+\mathrm{1}\right)\: \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{2}\:{prime}\:{numbers},\:{each}\:\mathrm{2},\:\mathrm{24}\:{times} \\ $$$${Case}\:\left(\mathrm{4}\right): \\ $$$${D}=\mathrm{75}=\left(\mathrm{74}+\mathrm{1}\right) \\ $$$$\Rightarrow\:{we}\:{need}\:\mathrm{1}\:{prime}\:{number}\:\mathrm{74}\:{times} \\ $$$$ \\ $$$${Case}\:\left(\mathrm{4}\right)\:{is}\:{not}\:{suitable},\:{since}\:{we}\:{need}\:{at}\:{least} \\ $$$$\mathrm{2}\:{prime}\:{numbers}:\:\mathrm{3}×\mathrm{5}^{\mathrm{2}} . \\ $$$$ \\ $$$${To}\:{keep}\:{n}\:{small}\:{we}\:{should}\:{use}\:{as}\:{many} \\ $$$${smaller}\:{prime}\:{numbers}\:{as}\:{possible}. \\ $$$$ \\ $$$${Case}\:\left(\mathrm{1}\right):\: \\ $$$$\mathrm{3}\:{prime}\:{numbers}\:\left({each}\:\mathrm{2},\:\mathrm{4},\:\mathrm{4}\:{times}\right) \\ $$$$\Rightarrow\:{n}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{4}} ×\mathrm{5}^{\mathrm{2}} =\mathrm{32}\:\mathrm{400} \\ $$$${Case}\:\left(\mathrm{2}\right):\: \\ $$$$\mathrm{2}\:{prime}\:{numbers}\:\left({each}\:\mathrm{4},\:\mathrm{14}\:{times}\right) \\ $$$$\Rightarrow\:{n}=\mathrm{3}^{\mathrm{14}} ×\mathrm{5}^{\mathrm{4}} =\mathrm{2}\:\mathrm{989}\:\mathrm{355}\:\mathrm{625} \\ $$$${Case}\:\left(\mathrm{3}\right):\: \\ $$$$\mathrm{2}\:{prime}\:{numbers}\:\left({each}\:\mathrm{2},\:\mathrm{24}\:{times}\right) \\ $$$$\Rightarrow\:{n}=\mathrm{3}^{\mathrm{24}} ×\mathrm{5}^{\mathrm{2}} =\mathrm{7}\:\mathrm{060}\:\mathrm{738}\:\mathrm{412}\:\mathrm{025} \\ $$$$ \\ $$$${Case}\:\left(\mathrm{1}\right)\:{gives}\:{the}\:{smallest}\:{n}\:{which}\:{is} \\ $$$${n}=\mathrm{32400} \\ $$$$ \\ $$$$=\:{END}\:= \\ $$

Commented by Joel576 last updated on 13/Mar/17

Hi, mrW1 Thank you very much for your great solution Even my teacher, he haven′t found any solutions yet. Glad you wanted to spend your time to find the solution.

$${Hi},\:\mathrm{mrW1} \\ $$$${Thank}\:{you}\:{very}\:{much}\:{for}\:{your}\:{great}\:{solution} \\ $$$${Even}\:{my}\:{teacher},\:{he}\:{haven}'{t}\:{found}\:{any}\:{solutions}\:{yet}. \\ $$$${Glad}\:{you}\:{wanted}\:{to}\:{spend}\:{your}\:{time}\:{to}\:{find}\:{the}\:{solution}. \\ $$

Commented by FilupS last updated on 13/Mar/17

I think mrW1 is the smartest person on here in the widest range of maths. Do you goto collage/university? I am completely self study. Math is my hobby.

$$\mathrm{I}\:\mathrm{think}\:\mathrm{mrW1}\:\mathrm{is}\:\mathrm{the}\:\mathrm{smartest}\:\mathrm{person}\:\mathrm{on} \\ $$$$\mathrm{here}\:\mathrm{in}\:\mathrm{the}\:\mathrm{widest}\:\mathrm{range}\:\mathrm{of}\:\mathrm{maths}.\:\mathrm{Do}\:\mathrm{you} \\ $$$$\mathrm{goto}\:\mathrm{collage}/\mathrm{university}?\:\mathrm{I}\:\mathrm{am}\:\mathrm{completely} \\ $$$$\mathrm{self}\:\mathrm{study}.\:\mathrm{Math}\:\mathrm{is}\:\mathrm{my}\:\mathrm{hobby}. \\ $$

Commented by FilupS last updated on 13/Mar/17

My strongest topic is in sequences and in number theory. I want to learn linear algebra

$$\mathrm{My}\:\mathrm{strongest}\:\mathrm{topic}\:\mathrm{is}\:\mathrm{in}\:\mathrm{sequences}\:\mathrm{and}\:\mathrm{in} \\ $$$$\mathrm{number}\:\mathrm{theory}.\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{linear} \\ $$$$\mathrm{algebra} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com