
Question Number 110797 by ZiYangLee last updated on 30/Aug/20
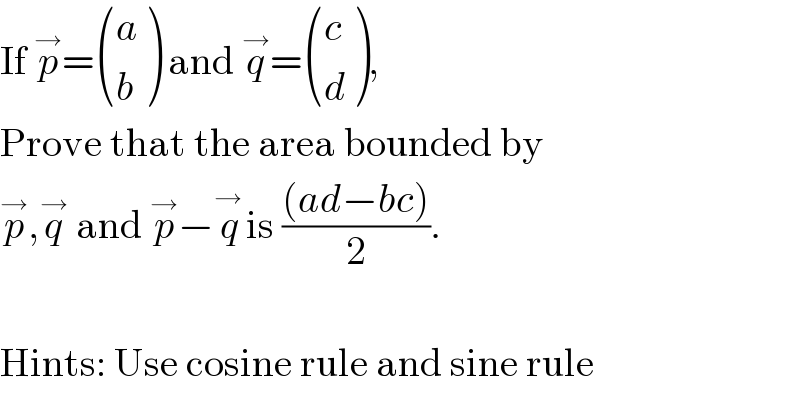
$$\mathrm{If}\:\overset{\rightarrow} {{p}}=\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}\:\mathrm{and}\:\overset{\rightarrow} {{q}}=\begin{pmatrix}{{c}}\\{{d}}\end{pmatrix}, \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{area}\:\mathrm{bounded}\:\mathrm{by}\: \\ $$$$\overset{\rightarrow} {{p}},\overset{\rightarrow} {{q}}\:\mathrm{and}\:\overset{\rightarrow} {{p}}−\overset{\rightarrow\:} {{q}}\mathrm{is}\:\frac{\left({ad}−{bc}\right)}{\mathrm{2}}. \\ $$$$ \\ $$$$\mathrm{Hints}:\:\mathrm{Use}\:\mathrm{cosine}\:\mathrm{rule}\:\mathrm{and}\:\mathrm{sine}\:\mathrm{rule} \\ $$
Commented by kaivan.ahmadi last updated on 30/Aug/20
![let θ be the angel between p^→ and q^→ p^→ −q^→ = (((a−c)),((b−d)) ) ∣p^→ −q^→ ∣^2 =∣p^→ ∣^2 +∣q^→ ∣^2 −2∣p^→ ∣.∣q^→ ∣.cosθ⇒ (a−c)^2 +(b−d)^2 =a^2 +b^2 +c^2 +d^2 −2(√(a^2 +b^2 )).(√(c^2 +d^2 )).cosθ ⇒−ac−bd=(√((a^2 +b^2 )(c^2 +d^2 ))).cosθ⇒ cosθ=((−ac−bd)/(√((a^2 +b^2 )(c^2 +d^2 ))))⇒sinθ=(√(1−(((ac−bd)^2 )/((a^2 +b^2 )(c^2 +d^2 )))))= (√(((a^2 +b^2 )(c^2 +d^2 )−(ac−bd)^2 )/((a^2 +b^2 )(c^2 +d^2 ))))=(√((a^2 d^2 +b^2 c^2 −2abcd)/((a^2 +b^2 )(c^2 +d^2 ))))= (√(((ad−bc)^2 )/((a^2 +b^2 )(c^2 +d^2 ))))=(((ad−bc))/(∣p^→ ∣.∣q^→ ∣)) ;[ad−bc≥0] now we have S=(1/2)∣p^→ ∣.∣q^→ ∣.sinθ=(1/2)∣p^→ ∣.∣q^→ ∣.(((ad−bc))/(∣p^→ ∣.∣q^→ ∣))=(1/2)(ad−bc)](Q110825.png)
$${let}\:\theta\:{be}\:{the}\:{angel}\:{between}\:\overset{\rightarrow} {{p}}\:{and}\:\overset{\rightarrow} {{q}}\: \\ $$$$ \\ $$$$\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}=\begin{pmatrix}{{a}−{c}}\\{{b}−{d}}\end{pmatrix} \\ $$$$\mid\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\mid^{\mathrm{2}} =\mid\overset{\rightarrow} {{p}}\mid^{\mathrm{2}} +\mid\overset{\rightarrow} {{q}}\mid^{\mathrm{2}} −\mathrm{2}\mid\overset{\rightarrow} {{p}}\mid.\mid\overset{\rightarrow} {{q}}\mid.{cos}\theta\Rightarrow \\ $$$$\left({a}−{c}\right)^{\mathrm{2}} +\left({b}−{d}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }.\sqrt{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }.{cos}\theta \\ $$$$\Rightarrow−{ac}−{bd}=\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}.{cos}\theta\Rightarrow \\ $$$${cos}\theta=\frac{−{ac}−{bd}}{\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}}\Rightarrow{sin}\theta=\sqrt{\mathrm{1}−\frac{\left({ac}−{bd}\right)^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}}= \\ $$$$\sqrt{\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)−\left({ac}−{bd}\right)^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}}=\sqrt{\frac{{a}^{\mathrm{2}} {d}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{2}{abcd}}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}}= \\ $$$$\sqrt{\frac{\left({ad}−{bc}\right)^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}}=\frac{\left({ad}−{bc}\right)}{\mid\overset{\rightarrow} {{p}}\mid.\mid\overset{\rightarrow} {{q}}\mid}\:\:;\left[{ad}−{bc}\geqslant\mathrm{0}\right] \\ $$$${now}\:{we}\:{have} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\mid\overset{\rightarrow} {{p}}\mid.\mid\overset{\rightarrow} {{q}}\mid.{sin}\theta=\frac{\mathrm{1}}{\mathrm{2}}\mid\overset{\rightarrow} {{p}}\mid.\mid\overset{\rightarrow} {{q}}\mid.\frac{\left({ad}−{bc}\right)}{\mid\overset{\rightarrow} {{p}}\mid.\mid\overset{\rightarrow} {{q}}\mid}=\frac{\mathrm{1}}{\mathrm{2}}\left({ad}−{bc}\right) \\ $$
Commented by ZiYangLee last updated on 31/Aug/20

$$\mathrm{NICE} \\ $$
