(1)∫_e ^e^e ((ln (x).ln (ln (x)))/x) dx ? (2)lim_(x→π/4) ((cosec^2 x−2)/(cot x−1)) (3) Given { ((xy=((16y−9x)/(45)))),(((4/( (√x)))−(3/( (√y))) = 5)) :} ⇒find 9(√(xy))


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 110875 by bemath last updated on 31/Aug/20
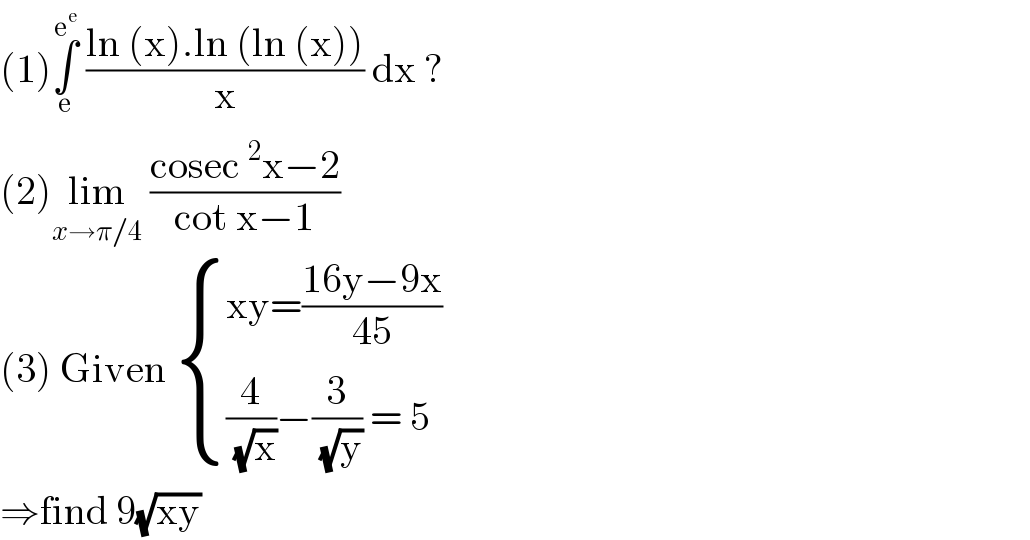
$(1)∫_e ^e^e ((ln (x).ln (ln (x)))/x) dx ? (2)lim_(x→π/4) ((cosec^2 x−2)/(cot x−1)) (3) Given { ((xy=((16y−9x)/(45)))),(((4/( (√x)))−(3/( (√y))) = 5)) :} ⇒find 9(√(xy))$
$(1) \underset{e}{\int^{e^{e}}} \frac{\ln (x) . \ln (\ln (x))}{x} dx ?$ $(2) \lim_{x \to π / 4} \frac{cosec^{2} x - 2}{\cot x - 1}$ $(3) Given {\begin{cases} xy = \frac{16 y - 9 x}{45} \\ \frac{4}{\sqrt{x}} - \frac{3}{\sqrt{y}} = 5 \end{cases}$ $\Rightarrow find 9 \sqrt{xy}$
	Answered by Dwaipayan Shikari last updated on 31/Aug/20

	$\int_{e}^{e^{e}} \frac{l o g (x) l o g (l o g (x))}{x} d x (l o g x = t, \frac{1}{x} = \frac{d t}{d x})$ $\int_{1}^{e} t l o g (t) d t$ ${[l o g t . \frac{t^{2}}{2}]}_{1}^{e} - \int_{1}^{e} \frac{t}{2} = \frac{e^{2}}{2} - \frac{e^{2}}{4} + \frac{1}{4} = \frac{1}{4} (e^{2} + 1)$
	Commented by bemath last updated on 31/Aug/20

	$thank you sir .$
	Commented by bemath last updated on 31/Aug/20

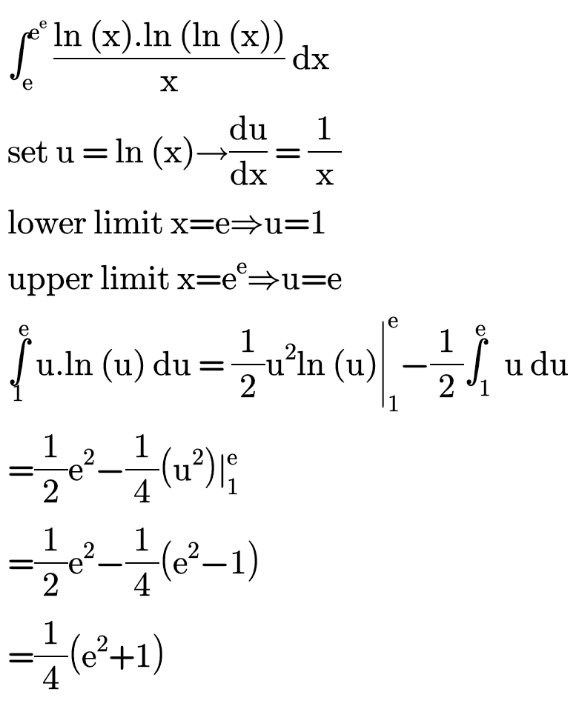
	Answered by Dwaipayan Shikari last updated on 31/Aug/20

	$2) \lim_{x \to \frac{π}{4}} \frac{1 - 2 {s i n}^{2} x}{{s i n}^{2} x (c o s x - s i n x)} . s i n x = \lim_{x \to \frac{π}{4}} \frac{{c o s}^{2} x - {s i n}^{2} x}{s i n x (c o s x - s i n x)} = \sqrt{2} . (s i n x + c o s x)$ $= 2$
	Commented by bemath last updated on 31/Aug/20

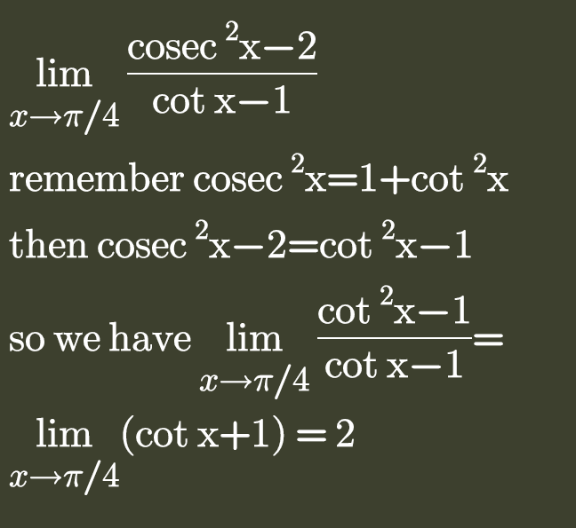
	Answered by bobhans last updated on 31/Aug/20
	$(3) { ((45=((16y−9x)/(xy))=((16)/x)−(9/9)=((4/( (√x))))^2 −((3/( (√y))))^2 )),(((4/( (√x)))−(3/( (√y))) = 5)) :} { ((45=((4/( (√x)))−(3/( (√y))))((4/( (√x)))+(3/( (√y))))...(i))),((5=(4/( (√x)))−(3/( (√y)))...(ii))) :} ⇔ 45 = 5((4/( (√x)))+(3/( (√y)))) ; (4/( (√x)))+(3/( (√y))) = 9...(iii) (i)+(iii)⇒ (8/( (√x))) = 14⇒(√x) = (4/7) and (3/( (√y)))=9−7 (√y) = (3/2). therefore 9(√(xy)) = 9×(4/7)×(3/2) = ((54)/7)$
	$(3) {\begin{cases} 45 = \frac{16 y - 9 x}{xy} = \frac{16}{x} - \frac{9}{9} = {(\frac{4}{\sqrt{x}})}^{2} - {(\frac{3}{\sqrt{y}})}^{2} \\ \frac{4}{\sqrt{x}} - \frac{3}{\sqrt{y}} = 5 \end{cases}$ ${\begin{cases} 45 = (\frac{4}{\sqrt{x}} - \frac{3}{\sqrt{y}}) (\frac{4}{\sqrt{x}} + \frac{3}{\sqrt{y}}) . . . (i) \\ 5 = \frac{4}{\sqrt{x}} - \frac{3}{\sqrt{y}} . . . (ii) \end{cases}$ $\Leftrightarrow 45 = 5 (\frac{4}{\sqrt{x}} + \frac{3}{\sqrt{y}}); \frac{4}{\sqrt{x}} + \frac{3}{\sqrt{y}} = 9 . . . (iii)$ $(i) + (iii) \Rightarrow \frac{8}{\sqrt{x}} = 14 \Rightarrow \sqrt{x} = \frac{4}{7} and \frac{3}{\sqrt{y}} = 9 - 7$ $\sqrt{y} = \frac{3}{2} . therefore 9 \sqrt{xy} = 9 \times \frac{4}{7} \times \frac{3}{2}$ $= \frac{54}{7}$
	Commented by bemath last updated on 31/Aug/20

	$thank you$
	Answered by mathmax by abdo last updated on 31/Aug/20
	$I =∫_e ^e^e ((ln(x)ln(lnx))/x) dx changement lnx =t give I =∫_1 ^e ((t ln(t))/e^t ) e^t dt =∫_1 ^e tln(t)dt =[(t^2 /2)ln(t)]_1 ^e −∫_1 ^e (t^2 /2)(dt/t) =(e^2 /2) −(1/2)∫_1 ^e t dt =(e^2 /2)−(1/2)[(t^2 /2)]_1 ^e =(e^2 /2)−(1/4){e^2 −1} =(e^2 /4) +(1/4) ⇒ I =((1+e^2 )/4)$
	$I = \int_{e}^{e^{e}} \frac{\ln (x) \ln (lnx)}{x} dx changement lnx = t give$ $I = \int_{1}^{e} \frac{t \ln (t)}{e^{t}} e^{t} dt = \int_{1}^{e} tln (t) dt = {[\frac{t^{2}}{2} \ln (t)]}_{1}^{e} - \int_{1}^{e} \frac{t^{2}}{2} \frac{dt}{t}$ $= \frac{e^{2}}{2} - \frac{1}{2} \int_{1}^{e} t dt = \frac{e^{2}}{2} - \frac{1}{2} {[\frac{t^{2}}{2}]}_{1}^{e} = \frac{e^{2}}{2} - \frac{1}{4} {e^{2} - 1} = \frac{e^{2}}{4} + \frac{1}{4} \Rightarrow$ $I = \frac{1 + e^{2}}{4}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum