
Question and Answers Forum
Question Number 110895 by Aina Samuel Temidayo last updated on 31/Aug/20
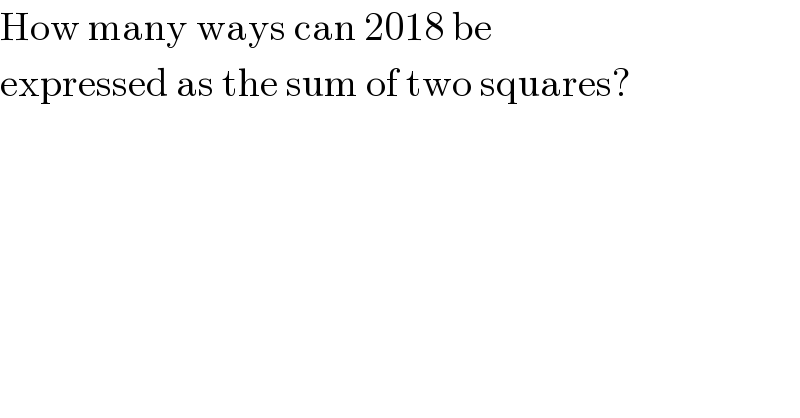
Answered by ajfour last updated on 31/Aug/20

Answered by floor(10²Eta[1]) last updated on 31/Aug/20

Commented by Aina Samuel Temidayo last updated on 31/Aug/20

Answered by Rasheed.Sindhi last updated on 01/Sep/20
![(i) unit-digits. (ii)squares of unit-digits. (iii)unit-digits of squares [(( (i)),0,1,2,3,( 4),( 5),( 6),( 7),( 8),( 9)),(( (ii)),0,1,4,9,(16),(25),(36),(49),(64),(81)),(((iii)),0,1,4,9,( 6),( 5),( 6),( 9),( 4),( 1)) ] is sum of two square numbers. Hence its unit-digit(8) is made up of sum of unit-digits of squares Only two possibilities: 4+4=8 & 9+9=18 ^• 4 is square of unit-digits: 2 & 8 ^• 9 is square of unit-digits: 3 & 7 Search for the numbers is narrow enough now: Only numbers with units 2,8,3 & 7 So finally 3 is successful candidate. If n is one possible candidate for required numbers other number N is N=(√(2018−n)) provided that 2018−n is prefect squre. Finally 13^2 +43^2 =2018 only solution.](Q110981.png)
Commented by floor(10²Eta[1]) last updated on 01/Sep/20

Commented by Rasheed.Sindhi last updated on 01/Sep/20

