
Question and Answers Forum
Question Number 110964 by mathdave last updated on 01/Sep/20
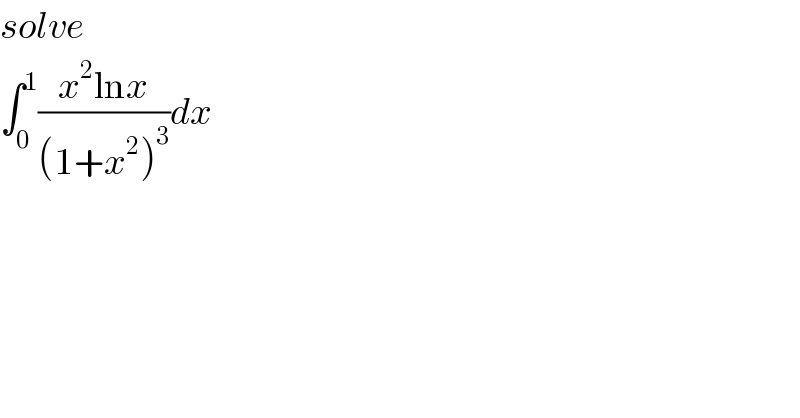
Answered by mathdave last updated on 01/Sep/20
![enjoy my solution let x=tany,dx=(1+tan^2 y)dy I=∫_0 ^(π/4) ((tanyln(tany))/((1+tan^2 y)^3 ))×(1+tan^2 y)dy I=∫_0 ^(π/4) ((tan^2 yln(tany))/(sec^4 y))dy=∫_0 ^(π/4) ((tan^2 yln(tany)cos^4 y)/1)dy I=∫_0 ^(π/4) (sinycosy)^2 ln(tany)dy but sinycosy=((sin2y)/2) I=(1/4)∫_0 ^(π/4) sin^2 2yln(tany)dy but cos4y=1−2sin^2 2y,sin^2 2y=((1−cos4y)/2) I=(1/8)∫_0 ^(π/4) (1−cos4y)ln(tany)dy I=(1/8)∫_0 ^(π/4) ln(tany)−(1/8)∫_0 ^(π/4) cos4yln(tany)dy let B=∫_0 ^(π/4) cos4yln(tany)dy using IBP but let ∫dv=∫cos4ydy,v=((sin4y)/4),u=ln(tany),du=((sec^2 y)/(tany))=(1/(sinycosy))=(2/(sin2y)) B=(1/4)[sin4yln(tany)]_0 ^(π/4) −(1/4)∫_0 ^(π/4) ((2sin4y)/(sin2y))dy B=−(1/2)∫_0 ^(π/4) ((sin4y)/(sin2y))dy (let 2y=x,dy=(dx/2)) =−(1/4)∫_0 ^(π/2) ((sin2x)/(sinx))dx=−(1/4)∫_0 ^(π/2) ((2sinxcosx)/(sinx))dx B=−(1/2)∫_0 ^(π/2) cosxdx=−(1/2)[sinx]_0 ^(π/2) =−(1/2) ∵B=∫_0 ^(π/4) cos4yln(tany)dy=−(1/2).........(1) then letA=∫_0 ^(π/4) ln(tany)dy let x=tany,dy=(dx/(1+x^2 )) A=∫_0 ^1 ((lnx)/(1+x^2 ))dx (using series summation) A=∫_0 ^1 (−1)^n Σ_(n=0) ^∞ x^(2n) lnxdx=(−1)^n Σ_(n=0) ^∞ ∫_0 ^1 x^(2n) .x^a dx∣_(a=0) (∂/∂a)∣_(a=0) A(a)=(−1)^n Σ_(n=0) ^∞ (∂/∂a)∫_0 ^1 x^(2n+a) dx (∂/∂a)∣_(a=0) A(a)=(−1)^n (∂/∂a)Σ_(n=0) ^∞ [(1/((2n+a+1)))] A(0)=A=−Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))=−G(catalan constant).....(2) but I=(1/8)A−(1/8)B=[−(G/8)−(1/8)(−(1/2))]=[(1/(16))−(1/8)G] ∵∫_0 ^1 ((x^2 lnx)/((1+x^2 )^3 ))dx=[(1/(16))−(1/8)G] solution by mathdave(1/09/2020)](Q110974.png)
Commented by mnjuly1970 last updated on 01/Sep/20

| ||
Question and Answers Forum | ||
Question Number 110964 by mathdave last updated on 01/Sep/20 | ||
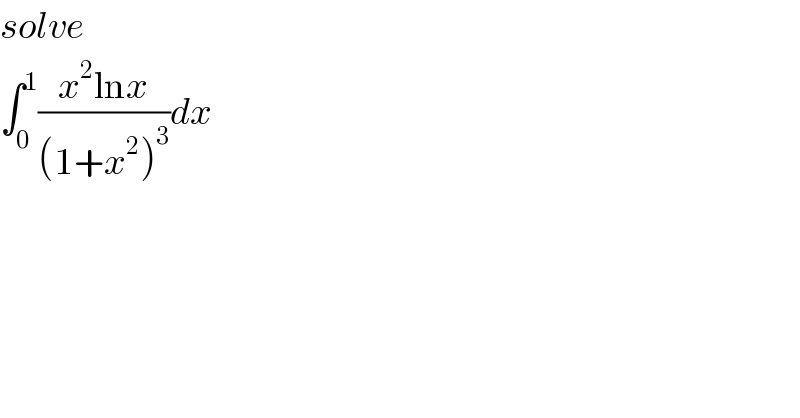 | ||
Answered by mathdave last updated on 01/Sep/20 | ||
![enjoy my solution let x=tany,dx=(1+tan^2 y)dy I=∫_0 ^(π/4) ((tanyln(tany))/((1+tan^2 y)^3 ))×(1+tan^2 y)dy I=∫_0 ^(π/4) ((tan^2 yln(tany))/(sec^4 y))dy=∫_0 ^(π/4) ((tan^2 yln(tany)cos^4 y)/1)dy I=∫_0 ^(π/4) (sinycosy)^2 ln(tany)dy but sinycosy=((sin2y)/2) I=(1/4)∫_0 ^(π/4) sin^2 2yln(tany)dy but cos4y=1−2sin^2 2y,sin^2 2y=((1−cos4y)/2) I=(1/8)∫_0 ^(π/4) (1−cos4y)ln(tany)dy I=(1/8)∫_0 ^(π/4) ln(tany)−(1/8)∫_0 ^(π/4) cos4yln(tany)dy let B=∫_0 ^(π/4) cos4yln(tany)dy using IBP but let ∫dv=∫cos4ydy,v=((sin4y)/4),u=ln(tany),du=((sec^2 y)/(tany))=(1/(sinycosy))=(2/(sin2y)) B=(1/4)[sin4yln(tany)]_0 ^(π/4) −(1/4)∫_0 ^(π/4) ((2sin4y)/(sin2y))dy B=−(1/2)∫_0 ^(π/4) ((sin4y)/(sin2y))dy (let 2y=x,dy=(dx/2)) =−(1/4)∫_0 ^(π/2) ((sin2x)/(sinx))dx=−(1/4)∫_0 ^(π/2) ((2sinxcosx)/(sinx))dx B=−(1/2)∫_0 ^(π/2) cosxdx=−(1/2)[sinx]_0 ^(π/2) =−(1/2) ∵B=∫_0 ^(π/4) cos4yln(tany)dy=−(1/2).........(1) then letA=∫_0 ^(π/4) ln(tany)dy let x=tany,dy=(dx/(1+x^2 )) A=∫_0 ^1 ((lnx)/(1+x^2 ))dx (using series summation) A=∫_0 ^1 (−1)^n Σ_(n=0) ^∞ x^(2n) lnxdx=(−1)^n Σ_(n=0) ^∞ ∫_0 ^1 x^(2n) .x^a dx∣_(a=0) (∂/∂a)∣_(a=0) A(a)=(−1)^n Σ_(n=0) ^∞ (∂/∂a)∫_0 ^1 x^(2n+a) dx (∂/∂a)∣_(a=0) A(a)=(−1)^n (∂/∂a)Σ_(n=0) ^∞ [(1/((2n+a+1)))] A(0)=A=−Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))=−G(catalan constant).....(2) but I=(1/8)A−(1/8)B=[−(G/8)−(1/8)(−(1/2))]=[(1/(16))−(1/8)G] ∵∫_0 ^1 ((x^2 lnx)/((1+x^2 )^3 ))dx=[(1/(16))−(1/8)G] solution by mathdave(1/09/2020)](Q110974.png) | ||
| ||
Commented by mnjuly1970 last updated on 01/Sep/20 | ||
 | ||