
Question and Answers Forum
Question Number 111024 by mathmax by abdo last updated on 01/Sep/20
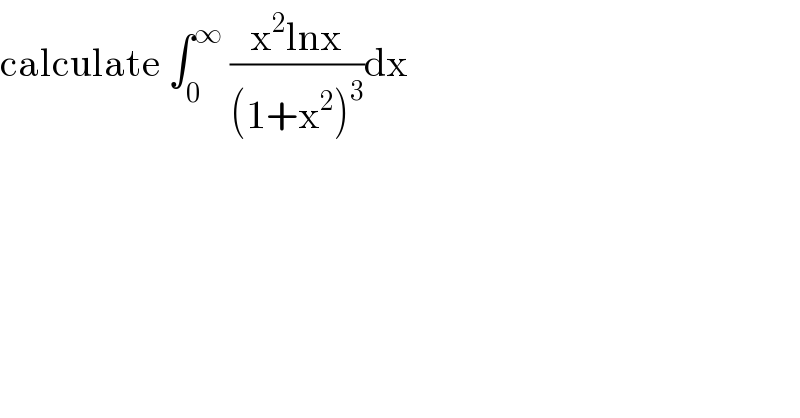
Answered by mathdave last updated on 01/Sep/20
![solution let I=∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx then (∂/∂a)∣_(a=0) I(a)=(1/4)(∂/∂a)∫_0 ^∞ (x^((1/2)+a) /((1+x)^3 ))dx I^1 (a)=(1/4)(∂/∂a)β((3/2)+a,(3/2)−a)=(1/4)(∂/∂a)[((Γ((3/2)+a)Γ((3/2)−a))/(Γ(3)))] I^′ (0)=(1/4)•((Γ((3/2))Γ((3/2)))/(Γ(3)))[ψ((3/2))−ψ((3/2))]=0 ∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx=0 mathdave(01/09/2020)](Q111037.png)
Commented by abdomsup last updated on 01/Sep/20

| ||
Question and Answers Forum | ||
Question Number 111024 by mathmax by abdo last updated on 01/Sep/20 | ||
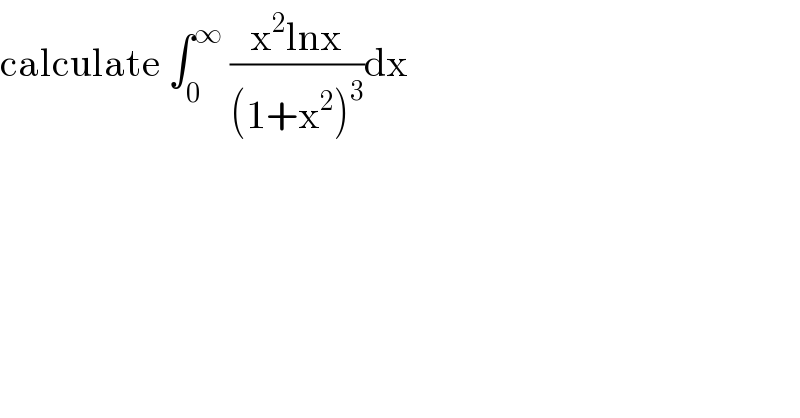 | ||
Answered by mathdave last updated on 01/Sep/20 | ||
![solution let I=∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx then (∂/∂a)∣_(a=0) I(a)=(1/4)(∂/∂a)∫_0 ^∞ (x^((1/2)+a) /((1+x)^3 ))dx I^1 (a)=(1/4)(∂/∂a)β((3/2)+a,(3/2)−a)=(1/4)(∂/∂a)[((Γ((3/2)+a)Γ((3/2)−a))/(Γ(3)))] I^′ (0)=(1/4)•((Γ((3/2))Γ((3/2)))/(Γ(3)))[ψ((3/2))−ψ((3/2))]=0 ∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx=0 mathdave(01/09/2020)](Q111037.png) | ||
| ||
Commented by abdomsup last updated on 01/Sep/20 | ||
 | ||