
Question and Answers Forum
Question Number 111025 by mathmax by abdo last updated on 01/Sep/20
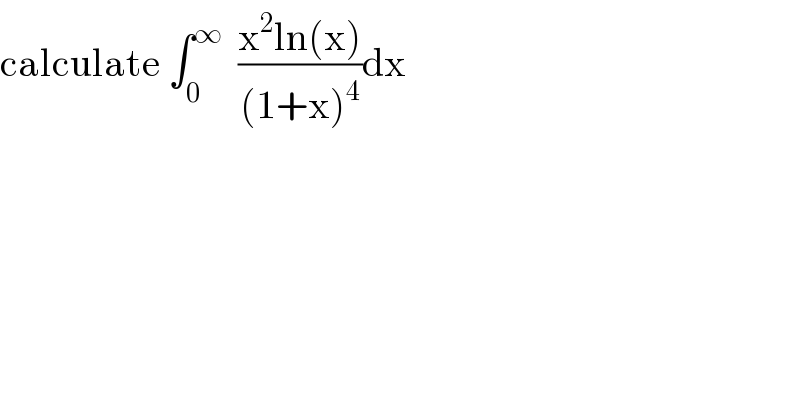
Answered by mathdave last updated on 01/Sep/20
![solution let I=∫_0 ^∞ ((x^2 ln(x))/((1+x)^4 ))dx I(a)=(∂/∂a)∫_0 ^∞ (x^(2+a) /((1+x)^4 ))dx (∂/∂a)∣_(a=0) I(a)=(∂/∂a)β(3+a,1−a)=(∂/∂a)[((Γ(3+a)Γ(1−a))/(Γ(4)))] I^′ (a)=((Γ(3+a)Γ(1−a))/(Γ(4)))[ψ(3+a)−ψ(1−a)] I^′ (0)=((Γ(3)Γ(1))/(Γ(4)))[ψ(3)−ψ(1)] I^′ (0)=(1/3)[(3/2)−γ+γ]=(1/2) ∵∫_0 ^∞ ((x^2 lnx)/((1+x)^4 ))dx=(1/2) mathdave](Q111031.png)
| ||
Question and Answers Forum | ||
Question Number 111025 by mathmax by abdo last updated on 01/Sep/20 | ||
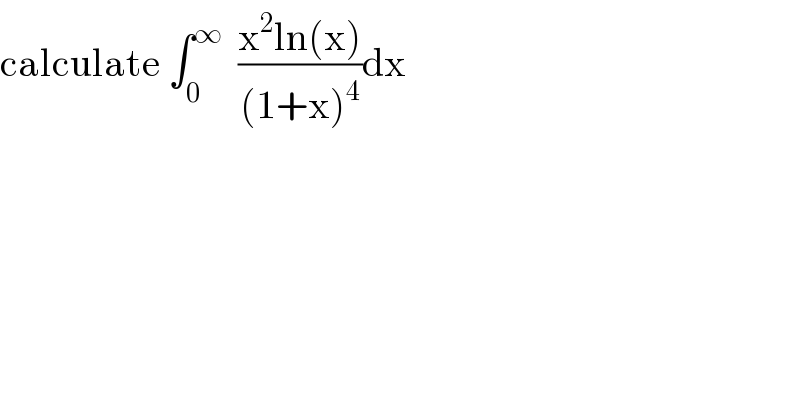 | ||
Answered by mathdave last updated on 01/Sep/20 | ||
![solution let I=∫_0 ^∞ ((x^2 ln(x))/((1+x)^4 ))dx I(a)=(∂/∂a)∫_0 ^∞ (x^(2+a) /((1+x)^4 ))dx (∂/∂a)∣_(a=0) I(a)=(∂/∂a)β(3+a,1−a)=(∂/∂a)[((Γ(3+a)Γ(1−a))/(Γ(4)))] I^′ (a)=((Γ(3+a)Γ(1−a))/(Γ(4)))[ψ(3+a)−ψ(1−a)] I^′ (0)=((Γ(3)Γ(1))/(Γ(4)))[ψ(3)−ψ(1)] I^′ (0)=(1/3)[(3/2)−γ+γ]=(1/2) ∵∫_0 ^∞ ((x^2 lnx)/((1+x)^4 ))dx=(1/2) mathdave](Q111031.png) | ||
| ||