
Question and Answers Forum
Question Number 111080 by bemath last updated on 02/Sep/20
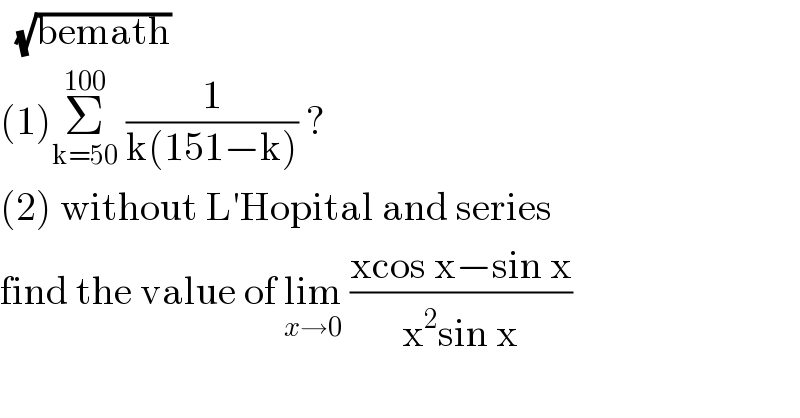
Answered by john santu last updated on 02/Sep/20
![(2) lim_(x→0) ((xcos x−sin x+x−x)/(x^2 sin x)) = lim_(x→0) ((x(cos x−1))/(x^2 sin x))+lim_(x→0) ((x−sin x)/(x^2 sin x)) = the first term L_1 = lim_(x→0) ((x(cos x−1))/(x^2 sin x))=lim_(x→0) ((cos x−1)/(xsin x)) L_1 =lim_(x→0) ((−2sin^2 ((x/2)))/(xsin x))=−2×(1/4)=−(1/2) the second term L_2 = lim_(x→0) ((x−sin x)/(x^2 sin x)) = lim_(x→0) ((x−sin x)/x^3 ) .(x/(sin x)) [ note that lim_(x→0) (x/(sin x)) = 1 ] L_2 =lim_(x→0) ((x−sin x)/x^3 ) = (1/6) [ we can find it by letting x = 2t ] Hence , we conclude that lim_(x→0) ((xcos x−sin x)/(x^2 sin x)) = −(1/2)+(1/6)=−(1/3)](Q111081.png)
Commented by bemath last updated on 02/Sep/20

| ||
Question and Answers Forum | ||
Question Number 111080 by bemath last updated on 02/Sep/20 | ||
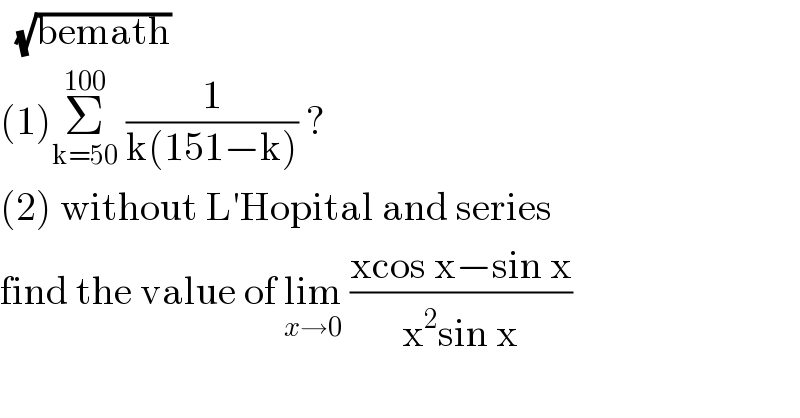 | ||
Answered by john santu last updated on 02/Sep/20 | ||
![(2) lim_(x→0) ((xcos x−sin x+x−x)/(x^2 sin x)) = lim_(x→0) ((x(cos x−1))/(x^2 sin x))+lim_(x→0) ((x−sin x)/(x^2 sin x)) = the first term L_1 = lim_(x→0) ((x(cos x−1))/(x^2 sin x))=lim_(x→0) ((cos x−1)/(xsin x)) L_1 =lim_(x→0) ((−2sin^2 ((x/2)))/(xsin x))=−2×(1/4)=−(1/2) the second term L_2 = lim_(x→0) ((x−sin x)/(x^2 sin x)) = lim_(x→0) ((x−sin x)/x^3 ) .(x/(sin x)) [ note that lim_(x→0) (x/(sin x)) = 1 ] L_2 =lim_(x→0) ((x−sin x)/x^3 ) = (1/6) [ we can find it by letting x = 2t ] Hence , we conclude that lim_(x→0) ((xcos x−sin x)/(x^2 sin x)) = −(1/2)+(1/6)=−(1/3)](Q111081.png) | ||
| ||
Commented by bemath last updated on 02/Sep/20 | ||
 | ||