Question Number 111157 by mathdave last updated on 02/Sep/20
$${question}\:{proposed}\:{MN}\:{july}\:\mathrm{1970} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{tan}{x}\left(\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}\right)\right){dx} \\ $$$${my}\:{solution}\:{followed} \\ $$
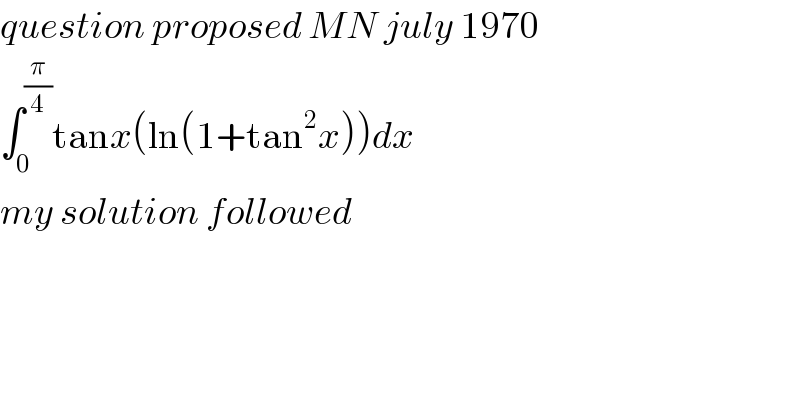
Answered by mathdave last updated on 02/Sep/20
![since 1+tan^2 x=sec^2 x let I=∫_0 ^(π/4) tanxln(sec^2 x)dx=2∫_0 ^(π/2) tanxln(secx)dx let u=ln(secx),du=tanxdx and dx=(1/(tanx))du I=2∫_0 ^(π/4) tanx×u×(1/(tanx))du=2∫_0 ^(π/4) udu I=2[(u^2 /2)]_0 ^(π/4) =2[((ln^2 (cosx))/2)]_0 ^(π/4) =[0−ln^2 ((1/(√2)))]=(1/4)ln^2 (2) ∵∫_0 ^(π/4) tanx(ln(1+tan^2 x))dx=(1/4)ln^2 (2) mathdave(02/09/2020)](Q111161.png)
$${since}\:\:\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}=\mathrm{sec}^{\mathrm{2}} {x} \\ $$$${let}\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{sec}^{\mathrm{2}} {x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{sec}{x}\right){dx} \\ $$$${let}\:\:{u}=\mathrm{ln}\left(\mathrm{sec}{x}\right),{du}=\mathrm{tan}{xdx}\:\:{and}\:{dx}=\frac{\mathrm{1}}{\mathrm{tan}{x}}{du} \\ $$$${I}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{tan}{x}×{u}×\frac{\mathrm{1}}{\mathrm{tan}{x}}{du}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {udu} \\ $$$${I}=\mathrm{2}\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\mathrm{2}\left[\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{cos}{x}\right)}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\left[\mathrm{0}−\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)\right]=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$$\because\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{tan}{x}\left(\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}\right)\right){dx}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right) \\ $$$${mathdave}\left(\mathrm{02}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by mnjuly1970 last updated on 02/Sep/20
$${thank}\:{you}\:{so}\:{much}\:{sir}....... \\ $$
Commented by mathdave last updated on 02/Sep/20
$${you}\:{are}\:{welcome} \\ $$
Answered by mathmax by abdo last updated on 02/Sep/20
![I =∫_0 ^(π/4) tanx(ln(1+tan^2 x))dx changement tanx =t give I =∫_0 ^1 tln(1+t^2 )(dt/(1+t^2 )) =_(by parts) [(1/2)ln(1+t^2 )ln(1+t^2 )]_0 ^1 −∫_0 ^1 (1/2)ln(1+t^2 )((2t)/(1+t^2 )) dt =(1/2)ln^2 (2)−∫_0 ^1 ((tln(1+t^2 ))/(1+t^2 ))dt =(1/2)ln^2 (2)−I ⇒2I =(1/2)ln^2 (2) ⇒★ I =(1/4)ln^2 (2)★](Q111257.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{tanx}\left(\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\right)\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{tanx}\:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{tln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{tln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\mathrm{I}\:\Rightarrow\mathrm{2I}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\:\Rightarrow\bigstar\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\bigstar \\ $$
Commented by mnjuly1970 last updated on 03/Sep/20
$${very}\:{nice}\:{thank}\:{you}\:{master}... \\ $$