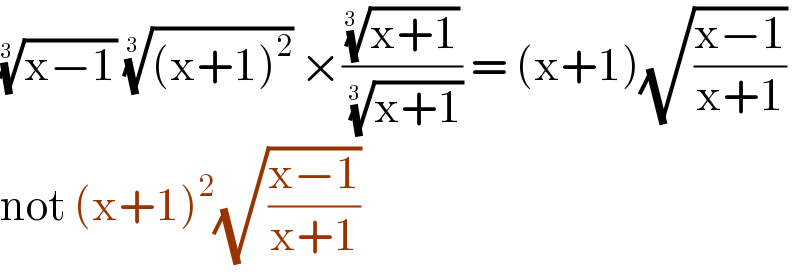Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 111195 by bemath last updated on 02/Sep/20

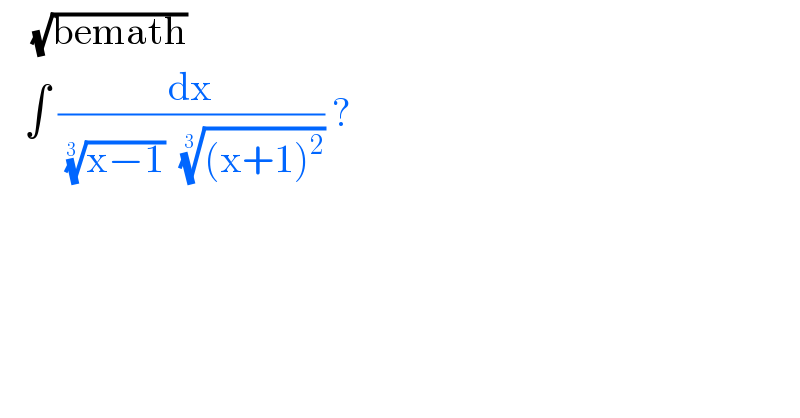
(√(bemath)) ∫ (dx/( ((x−1))^(1/(3 )) (((x+1)^2 ))^(1/(3 )) )) ?

$$\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\:\:\:\int\:\frac{\mathrm{dx}}{\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{1}}\:\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }}\:? \\ $$

Answered by Sarah85 last updated on 02/Sep/20

substitute t=(((x−1)/(x+1)))^(1/3) ⇔ x=−((t^3 +1)/(t^3 −1)) ⇒ ⇒ dx=(3/2)(((x−1)^2 (x+2)^4 ))^(1/3) dt ⇒ −3∫(t/(t^3 −1))dt=−∫(dt/(t−1))+∫((t−1)/(t^2 +t+1))dt= =−ln (t−1) +(1/2)ln (t^2 +t+1) −(√3)arctan ((2t+1)/( (√3))) = =(1/2)ln ((t^2 +t+1)/((t−1)^2 )) −(√3)arctan ((2t+1)/( (√3))) ...

$$\mathrm{substitute}\:{t}=\sqrt[{\mathrm{3}}]{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}\:\Leftrightarrow\:{x}=−\frac{{t}^{\mathrm{3}} +\mathrm{1}}{{t}^{\mathrm{3}} −\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:{dx}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{2}\right)^{\mathrm{4}} }{dt} \\ $$$$\Rightarrow \\ $$$$−\mathrm{3}\int\frac{{t}}{{t}^{\mathrm{3}} −\mathrm{1}}{dt}=−\int\frac{{dt}}{{t}−\mathrm{1}}+\int\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$=−\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$... \\ $$

Commented by bemath last updated on 03/Sep/20

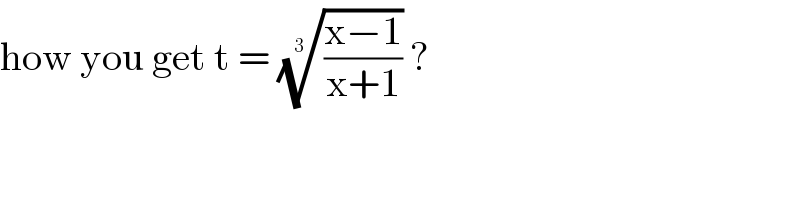
how you get t = (((x−1)/(x+1)))^(1/(3 )) ?

$$\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{t}\:=\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}\:? \\ $$

Commented by Sarah85 last updated on 03/Sep/20

try and error

$$\mathrm{try}\:\mathrm{and}\:\mathrm{error} \\ $$

Answered by mindispower last updated on 02/Sep/20

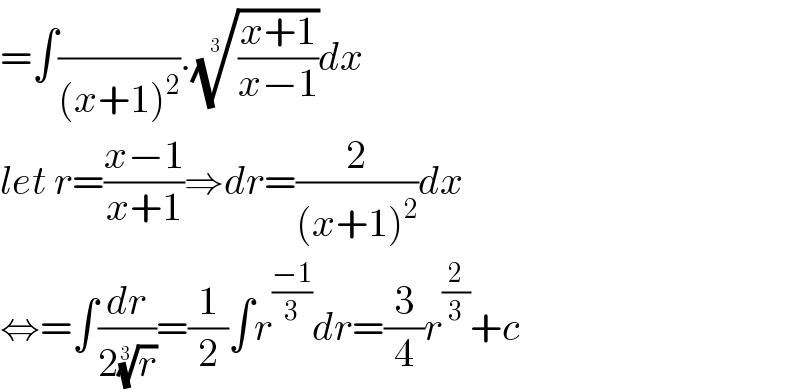
=∫(/((x+1)^2 )).(((x+1)/(x−1)))^(1/3) dx let r=((x−1)/(x+1))⇒dr=(2/((x+1)^2 ))dx ⇔=∫(dr/(2(r)^(1/3) ))=(1/2)∫r^((−1)/3) dr=(3/4)r^(2/3) +c

$$=\int\frac{}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }.\sqrt[{\mathrm{3}}]{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}{dx} \\ $$$${let}\:{r}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\Rightarrow{dr}=\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\Leftrightarrow=\int\frac{{dr}}{\mathrm{2}\sqrt[{\mathrm{3}}]{{r}}}=\frac{\mathrm{1}}{\mathrm{2}}\int{r}^{\frac{−\mathrm{1}}{\mathrm{3}}} {dr}=\frac{\mathrm{3}}{\mathrm{4}}{r}^{\frac{\mathrm{2}}{\mathrm{3}}} +{c} \\ $$

Commented by Her_Majesty last updated on 02/Sep/20

something went wrong I think

$${something}\:{went}\:{wrong}\:{I}\:{think} \\ $$

Commented by bobhans last updated on 03/Sep/20

((x−1))^(1/(3 )) (((x+1)^2 ))^(1/(3 )) ×(((x+1))^(1/(3 )) /( ((x+1))^(1/(3 )) )) = (x+1)(√((x−1)/(x+1))) not (x+1)^2 (√((x−1)/(x+1)))

$$\sqrt[{\mathrm{3}\:}]{\mathrm{x}−\mathrm{1}}\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:×\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\mathrm{1}}}{\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\mathrm{1}}}\:=\:\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$$$\mathrm{not}\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com