Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 111498 by bemath last updated on 04/Sep/20

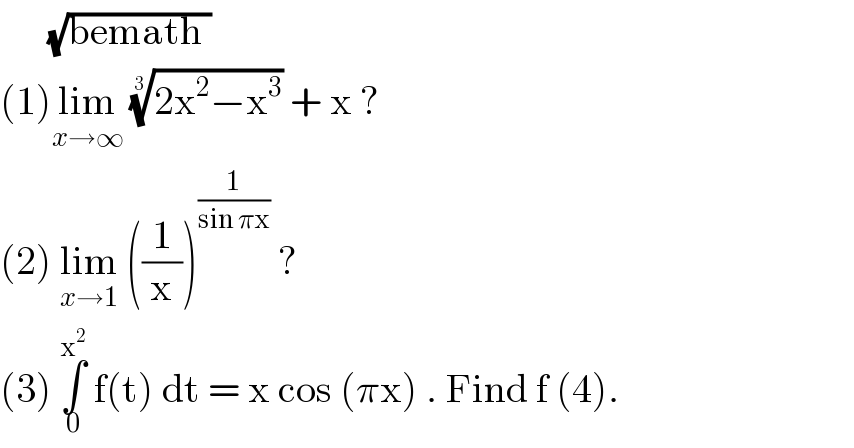
(√(bemath )) (1)lim_(x→∞) ((2x^2 −x^3 ))^(1/(3 )) + x ? (2) lim_(x→1) ((1/x))^(1/(sin πx)) ? (3) ∫_0 ^x^2 f(t) dt = x cos (πx) . Find f (4).

$$\:\:\:\:\:\:\sqrt{\mathrm{bemath}\:} \\ $$$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} }\:+\:\mathrm{x}\:? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\:\pi\mathrm{x}}} \:? \\ $$$$\left(\mathrm{3}\right)\:\underset{\mathrm{0}} {\overset{\mathrm{x}^{\mathrm{2}} } {\int}}\:\mathrm{f}\left(\mathrm{t}\right)\:\mathrm{dt}\:=\:\mathrm{x}\:\mathrm{cos}\:\left(\pi\mathrm{x}\right)\:.\:\mathrm{Find}\:\mathrm{f}\:\left(\mathrm{4}\right). \\ $$

Answered by john santu last updated on 04/Sep/20

let x = (1/t)→ { ((x→∞)),((t→0)) :} L=lim_(t→0) (((2/t^2 )−(1/t^3 )))^(1/(3 )) + (1/t) L= lim_(t→0) (((2t−1)/t^3 ))^(1/(3 )) + (1/t) L = lim_(t→0) ((((2t−1))^(1/(3 )) +1)/t) L= lim_(t→0) ((2t)/(t[ (2t−1)^2 −(2t−1)+1 ])) L= lim_(t→0) (2/((2t−1)^2 +2−2t)) = (2/3).

$$\:\:{let}\:{x}\:=\:\frac{\mathrm{1}}{{t}}\rightarrow\begin{cases}{{x}\rightarrow\infty}\\{{t}\rightarrow\mathrm{0}}\end{cases} \\ $$$${L}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{2}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }}\:+\:\frac{\mathrm{1}}{{t}} \\ $$$${L}=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{\mathrm{3}\:}]{\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{3}} }}\:+\:\frac{\mathrm{1}}{{t}} \\ $$$${L}\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{\mathrm{2}{t}−\mathrm{1}}+\mathrm{1}}{{t}} \\ $$$${L}=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{t}}{{t}\left[\:\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{2}{t}−\mathrm{1}\right)+\mathrm{1}\:\right]} \\ $$$${L}=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}}{\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}−\mathrm{2}{t}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}. \\ $$

Answered by bemath last updated on 04/Sep/20

Commented by bemath last updated on 04/Sep/20

typo in (x)^(1/(3 )) it should be (x^3 )^(1/(3 ))

$${typo}\:{in}\:\sqrt[{\mathrm{3}\:}]{{x}}\:{it}\:{should}\:{be}\:\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{3}} } \\ $$

Answered by john santu last updated on 04/Sep/20

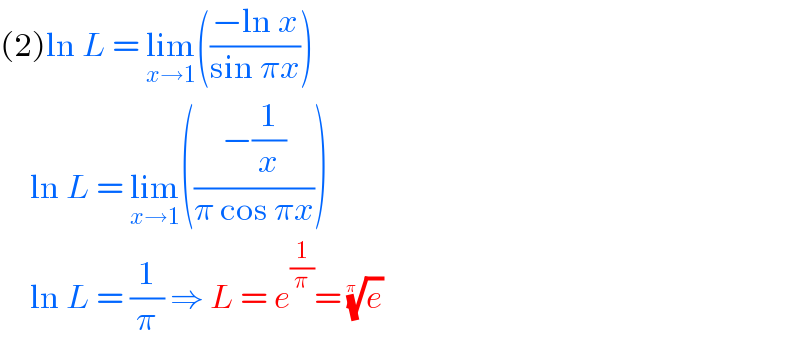
(2)ln L = lim_(x→1) (((−ln x)/(sin πx))) ln L = lim_(x→1) (((−(1/x))/(π cos πx))) ln L = (1/π) ⇒ L = e^(1/π) = (e)^(1/(π ))

$$\left(\mathrm{2}\right)\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{−\mathrm{ln}\:{x}}{\mathrm{sin}\:\pi{x}}\right) \\ $$$$\:\:\:\:\:\mathrm{ln}\:{L}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{−\frac{\mathrm{1}}{{x}}}{\pi\:\mathrm{cos}\:\pi{x}}\right) \\ $$$$\:\:\:\:\:\mathrm{ln}\:{L}\:=\:\frac{\mathrm{1}}{\pi}\:\Rightarrow\:{L}\:=\:{e}^{\frac{\mathrm{1}}{\pi}} =\:\sqrt[{\pi\:}]{{e}}\: \\ $$

Answered by john santu last updated on 04/Sep/20

(3) (d/dx) [∫_0 ^( x^2 ) f(t) dt ] = (d/dx) [x cos πx ] ⇒ 2x f(x^2 ) = cos πx −πx sin πx put x = 2 ⇒ 4f(4) = cos 2π−2π sin 2π ⇒ f(4) = (1/4)

$$\left(\mathrm{3}\right)\:\frac{{d}}{{dx}}\:\left[\int_{\mathrm{0}} ^{\:\:{x}^{\mathrm{2}} } {f}\left({t}\right)\:{dt}\:\right]\:=\:\frac{{d}}{{dx}}\:\left[{x}\:\mathrm{cos}\:\pi{x}\:\right] \\ $$$$\Rightarrow\:\mathrm{2}{x}\:{f}\left({x}^{\mathrm{2}} \right)\:=\:\mathrm{cos}\:\pi{x}\:−\pi{x}\:\mathrm{sin}\:\pi{x} \\ $$$${put}\:{x}\:=\:\mathrm{2}\: \\ $$$$\Rightarrow\:\mathrm{4}{f}\left(\mathrm{4}\right)\:=\:\mathrm{cos}\:\mathrm{2}\pi−\mathrm{2}\pi\:\mathrm{sin}\:\mathrm{2}\pi \\ $$$$\Rightarrow\:{f}\left(\mathrm{4}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Answered by mathmax by abdo last updated on 04/Sep/20

let f(x)=^3 (√(−x^3 +2x^2 )) +x ⇒f(x)=x−^3 (√(x^3 (1−(2/x)))) =x−x(1−(2/x))^(1/3) ∼x−x(1−(2/(3x))) ⇒f(x)∼(2/3) ⇒lim_(x→∞) f(x)=(2/3)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=^{\mathrm{3}} \sqrt{−\mathrm{x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{2}} }\:+\mathrm{x}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}−^{\mathrm{3}} \sqrt{\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}}\right)} \\ $$$$=\mathrm{x}−\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\sim\mathrm{x}−\mathrm{x}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3x}}\right)\:\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Answered by mathmax by abdo last updated on 04/Sep/20

2) let f(x) =((1/x))^(1/(sin(πx))) ⇒f(x) =e^((−lnx)/(sin(πx))) we have lim_(x→1) ((lnx)/(sin(πx))) =_(hospital) lim_(x→1) (1/(x(πcos(πx))) =−(1/π) ⇒ lim_(x→1) f(x) =e^(1/π) =^π (√e)

$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{x}}\right)^{\frac{\mathrm{1}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{−\mathrm{lnx}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}} \:\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{sin}\left(\pi\mathrm{x}\right)}\:=_{\mathrm{hospital}} \:\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{x}\left(\pi\mathrm{cos}\left(\pi\mathrm{x}\right)\right.}\:=−\frac{\mathrm{1}}{\pi}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\pi}} \:=^{\pi} \sqrt{\mathrm{e}} \\ $$

Commented by bobhans last updated on 04/Sep/20

typo e^(−(1/π)) = (1/e^(1/π) )

$$\mathrm{typo}\:\mathrm{e}^{−\frac{\mathrm{1}}{\pi}} \:=\:\frac{\mathrm{1}}{\mathrm{e}^{\frac{\mathrm{1}}{\pi}} } \\ $$

Commented by mathmax by abdo last updated on 04/Sep/20

no typo!

$$\mathrm{no}\:\mathrm{typo}! \\ $$

Commented by bobhans last updated on 04/Sep/20

why ? you got e^(−(1/π)) ? it not same to (e)^(1/(π )) ???

$$\mathrm{why}\:?\:\:\mathrm{you}\:\mathrm{got}\:\mathrm{e}^{−\frac{\mathrm{1}}{\pi}} \:?\:\mathrm{it}\:\mathrm{not}\:\mathrm{same}\:\mathrm{to}\: \\ $$$$\sqrt[{\pi\:}]{\mathrm{e}}\:??? \\ $$

Answered by mathmax by abdo last updated on 04/Sep/20

3) we have ∫_0 ^x^2 f(t)dt =xcos(πx) let derivate ⇒ 2xf(x^2 ) =cos(πx)−πxsin(πx) x=2 we get 4f(4) =cos(2π)−2π sin(2π) =1 ⇒f(4) =(1/4)

$$\left.\mathrm{3}\right)\:\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{xcos}\left(\pi\mathrm{x}\right)\:\:\mathrm{let}\:\mathrm{derivate}\:\Rightarrow \\ $$$$\mathrm{2xf}\left(\mathrm{x}^{\mathrm{2}} \right)\:=\mathrm{cos}\left(\pi\mathrm{x}\right)−\pi\mathrm{xsin}\left(\pi\mathrm{x}\right) \\ $$$$\mathrm{x}=\mathrm{2}\:\mathrm{we}\:\mathrm{get}\:\mathrm{4f}\left(\mathrm{4}\right)\:=\mathrm{cos}\left(\mathrm{2}\pi\right)−\mathrm{2}\pi\:\mathrm{sin}\left(\mathrm{2}\pi\right)\:=\mathrm{1}\:\Rightarrow\mathrm{f}\left(\mathrm{4}\right)\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Answered by Dwaipayan Shikari last updated on 04/Sep/20

lim_(x→1) ((1/x))^(1/(sinπx)) =y (1/(sinπx))log((1/x))=logy (((1/x)−1)/(sinπx)) ((log(1+(1/x)−1))/(((1/x)−1)))=logy lim_(w→0) (((1/(w+1))−1)/(sin(πw+π)))=logy lim_(w→0) (((−w)/(w+1))/(−sinπw))=logy lim_(x→0) (((−w)/(w+1))/(−wπ))=logy (1/π)=logy y=e^(1/π)

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}\right)^{\frac{\mathrm{1}}{{sin}\pi{x}}} ={y} \\ $$$$\frac{\mathrm{1}}{{sin}\pi{x}}{log}\left(\frac{\mathrm{1}}{{x}}\right)={logy} \\ $$$$\frac{\frac{\mathrm{1}}{{x}}−\mathrm{1}}{{sin}\pi{x}}\:\frac{{log}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}{\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}={logy} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{{w}+\mathrm{1}}−\mathrm{1}}{{sin}\left(\pi{w}+\pi\right)}={logy} \\ $$$$\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{−{w}}{{w}+\mathrm{1}}}{−{sin}\pi{w}}={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}{m}}\:\:\frac{\frac{−{w}}{{w}+\mathrm{1}}}{−{w}\pi}={logy} \\ $$$$\frac{\mathrm{1}}{\pi}={logy} \\ $$$${y}={e}^{\frac{\mathrm{1}}{\pi}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com