Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 111615 by mathdave last updated on 04/Sep/20

solve ∫(dx/((x^2 +2x+3)(√(x^2 +x+3))))

$${solve} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{3}}} \\ $$

Answered by mathmax by abdo last updated on 04/Sep/20

I =∫ (dx/((x^2 +2x+3)(√(x^2 +x+3)))) ⇒I =∫ (dx/((x^2 +x+3 +x)(√(x^2 +x+3)))) we have x^2 +x +3 =x^2 +((2x)/2) +(1/4) +3−(1/4) =(x+(1/2))^2 +((11)/4) we do the changement x+(1/2) =((√(11))/2) sh(t) ⇒ I =∫ (1/({((11)/4)sh^2 t +((11)/4) +((√(11))/2)sht−(1/2)}((√(11))/2)cht))((√(11))/2) sht dt =4∫ (dt/(11sh^2 t +11 +2(√(11))sht −2)) =4 ∫ (dt/(11sh^2 t +2(√(11))sht +9)) =4∫ (dt/(11((ch(2t)−1)/2)+2 (√(11))sh(t) +9)) 8 ∫ (dt/(11ch(2t)+4(√(11))sht +7)) =8 ∫ (dt/(11((e^(2t) +e^(−2t) )/2)+4(√(11))((e^t −e^(−t) )/2) +7)) =16 ∫ (dt/(11e^(2t) +11e^(−2t) +4(√(11))e^t −4(√(11))e^(−t) +14)) =_(e^t =z) 16 ∫ (dz/(z{ 11z^2 +11z^(−2) +4(√(11))z−4(√(11))z^(−1) +14})) =16 ∫ ((zdz)/(11z^4 +11 +4(√(11))z^3 −4(√(11))z+ 14z^2 )) =16 ∫ ((zdz)/(11z^4 +14z^2 +4(√(11))z^3 +11)) rest decomposition of f(z) =(z/(11z^4 +14z^2 +4(√(11))z^3 +11)) ....be continued....

$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{3}\right)\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{3}}}\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{3}\:+\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{3}}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}\:+\mathrm{3}\:=\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{2x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\:\mathrm{sh}\left(\mathrm{t}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{1}}{\left\{\frac{\mathrm{11}}{\mathrm{4}}\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:+\frac{\mathrm{11}}{\mathrm{4}}\:+\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{sht}−\frac{\mathrm{1}}{\mathrm{2}}\right\}\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{cht}}\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\:\mathrm{sht}\:\mathrm{dt} \\ $$$$=\mathrm{4}\int\:\:\frac{\mathrm{dt}}{\mathrm{11sh}^{\mathrm{2}} \mathrm{t}\:+\mathrm{11}\:+\mathrm{2}\sqrt{\mathrm{11}}\mathrm{sht}\:−\mathrm{2}}\:=\mathrm{4}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{11sh}^{\mathrm{2}} \mathrm{t}\:+\mathrm{2}\sqrt{\mathrm{11}}\mathrm{sht}\:+\mathrm{9}} \\ $$$$=\mathrm{4}\int\:\:\frac{\mathrm{dt}}{\mathrm{11}\frac{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{2}\:\sqrt{\mathrm{11}}\mathrm{sh}\left(\mathrm{t}\right)\:+\mathrm{9}} \\ $$$$\mathrm{8}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{11ch}\left(\mathrm{2t}\right)+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{sht}\:+\mathrm{7}}\:=\mathrm{8}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{11}\frac{\mathrm{e}^{\mathrm{2t}} \:+\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{11}}\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\:+\mathrm{7}} \\ $$$$=\mathrm{16}\:\int\:\frac{\mathrm{dt}}{\mathrm{11e}^{\mathrm{2t}} \:+\mathrm{11e}^{−\mathrm{2t}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{e}^{\mathrm{t}} −\mathrm{4}\sqrt{\mathrm{11}}\mathrm{e}^{−\mathrm{t}} \:+\mathrm{14}} \\ $$$$=_{\mathrm{e}^{\mathrm{t}} \:=\mathrm{z}} \:\:\:\mathrm{16}\:\int\:\:\frac{\mathrm{dz}}{\mathrm{z}\left\{\:\mathrm{11z}^{\mathrm{2}} +\mathrm{11z}^{−\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}−\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{−\mathrm{1}} \:+\mathrm{14}\right\}} \\ $$$$=\mathrm{16}\:\:\int\:\:\:\frac{\mathrm{zdz}}{\mathrm{11z}^{\mathrm{4}} \:+\mathrm{11}\:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{\mathrm{3}} −\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}+\:\mathrm{14z}^{\mathrm{2}} } \\ $$$$=\mathrm{16}\:\int\:\frac{\mathrm{zdz}}{\mathrm{11z}^{\mathrm{4}} +\mathrm{14z}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{\mathrm{3}} \:+\mathrm{11}}\:\:\mathrm{rest}\:\mathrm{decomposition}\:\mathrm{of} \\ $$$$\mathrm{f}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}}{\mathrm{11z}^{\mathrm{4}} \:+\mathrm{14z}^{\mathrm{2}} \:+\mathrm{4}\sqrt{\mathrm{11}}\mathrm{z}^{\mathrm{3}} \:+\mathrm{11}}\:....\mathrm{be}\:\mathrm{continued}.... \\ $$

Answered by Her_Majesty last updated on 05/Sep/20

∫(dx/((x^2 +2x+3)(√(x^2 +x+3))))= use t=((√(11))/(11))(2x+1+2(√(x^2 +x+3))) =((16)/(11))∫(t/(t^4 +(4/( (√(11))))t^3 +((14)/(11))t^2 −(4/( (√(11))))t+1))dt t^4 +(4/( (√(11))))t^3 +((14)/(11))t^2 −(4/( (√(11))))t+1= =(t^2 +(2/( (√(11))))(1+(√(2+3(√3))))t+((9+4(√3)+8(√(−1+(√3)))+2(√(2+2(√3))))/(11)))× ×(t^2 +(2/( (√(11))))(1−(√(2+2(√3))))t+((9+4(√3)−8(√(−1+(√3)))−2(√(2+2(√3))))/(11))) and I refuse to decompose it, sorry

$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{3}}}= \\ $$$${use}\:{t}=\frac{\sqrt{\mathrm{11}}}{\mathrm{11}}\left(\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{16}}{\mathrm{11}}\int\frac{{t}}{{t}^{\mathrm{4}} +\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}^{\mathrm{3}} +\frac{\mathrm{14}}{\mathrm{11}}{t}^{\mathrm{2}} −\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}+\mathrm{1}}{dt} \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}^{\mathrm{3}} +\frac{\mathrm{14}}{\mathrm{11}}{t}^{\mathrm{2}} −\frac{\mathrm{4}}{\:\sqrt{\mathrm{11}}}{t}+\mathrm{1}= \\ $$$$=\left({t}^{\mathrm{2}} +\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\left(\mathrm{1}+\sqrt{\mathrm{2}+\mathrm{3}\sqrt{\mathrm{3}}}\right){t}+\frac{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{8}\sqrt{−\mathrm{1}+\sqrt{\mathrm{3}}}+\mathrm{2}\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{11}}\right)× \\ $$$$×\left({t}^{\mathrm{2}} +\frac{\mathrm{2}}{\:\sqrt{\mathrm{11}}}\left(\mathrm{1}−\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}\right){t}+\frac{\mathrm{9}+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{8}\sqrt{−\mathrm{1}+\sqrt{\mathrm{3}}}−\mathrm{2}\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}}}{\mathrm{11}}\right) \\ $$$${and}\:{I}\:{refuse}\:{to}\:{decompose}\:{it},\:{sorry} \\ $$

Commented by mathdave last updated on 05/Sep/20

u c your life why cant u continue the solve has u know book ∙sorry u no nothing

$${u}\:{c}\:{your}\:{life}\:{why}\:{cant}\:{u}\:{continue}\:{the} \\ $$$${solve}\:{has}\:{u}\:{know}\:{book}\:\centerdot{sorry}\:{u}\:{no} \\ $$$${nothing} \\ $$

Commented by mathdave last updated on 05/Sep/20

has u antagonized my working i thought you will give correct evaluation no one is monopoly of knowledge ooo but am nt afraid to say u cant withstand me in mathematics

$${has}\:{u}\:{antagonized}\:{my}\:{working}\:{i} \\ $$$${thought}\:{you}\:{will}\:{give}\:{correct}\:{evaluation} \\ $$$${no}\:{one}\:{is}\:{monopoly}\:{of}\:{knowledge}\:{ooo} \\ $$$${but}\:{am}\:{nt}\:{afraid}\:{to}\:{say}\:{u}\:{cant} \\ $$$${withstand}\:{me}\:{in}\:{mathematics}\: \\ $$

Commented by Her_Majesty last updated on 05/Sep/20

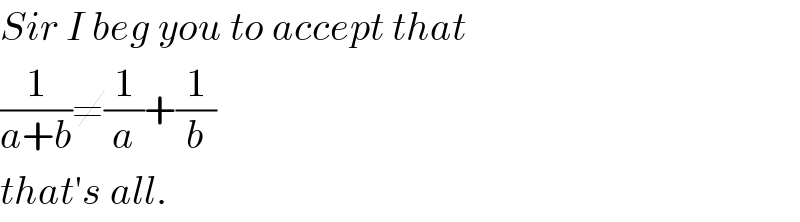
Sir I beg you to accept that (1/(a+b))≠(1/a)+(1/b) that′s all.

$${Sir}\:{I}\:{beg}\:{you}\:{to}\:{accept}\:{that} \\ $$$$\frac{\mathrm{1}}{{a}+{b}}\neq\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}} \\ $$$${that}'{s}\:{all}. \\ $$

Commented by Her_Majesty last updated on 05/Sep/20

btw I can continue but I don′t want to. obviously I′d have to decompose the fraction and solve 2 integrals of the form ∫((at+b)/(t^2 +αt+β))dt but I don′t waste my time with these given constants; I won′t gain any new experience doing so.

$${btw}\:{I}\:{can}\:{continue}\:{but}\:{I}\:{don}'{t}\:{want}\:{to}. \\ $$$${obviously}\:{I}'{d}\:{have}\:{to}\:{decompose}\:{the}\:{fraction} \\ $$$${and}\:{solve}\:\mathrm{2}\:{integrals}\:{of}\:{the}\:{form} \\ $$$$\int\frac{{at}+{b}}{{t}^{\mathrm{2}} +\alpha{t}+\beta}{dt}\:{but}\:{I}\:{don}'{t}\:{waste}\:{my}\:{time}\:{with} \\ $$$${these}\:{given}\:{constants};\:{I}\:{won}'{t}\:{gain}\:{any}\:{new} \\ $$$${experience}\:{doing}\:{so}. \\ $$

Commented by mathdave last updated on 05/Sep/20

tell me what i dont know for this am 101% (very)^(∞ ) and super correct

$${tell}\:{me}\:{what}\:{i}\:{dont}\:{know}\:{for}\:{this}\:{am} \\ $$$$\mathrm{101\%}\:\left({very}\right)^{\infty\:\:} {and}\:{super}\:{correct}\: \\ $$

Commented by mathdave last updated on 05/Sep/20

u most b very very stupid with that big mouth u just said u re mannerless

$${u}\:{most}\:{b}\:{very}\:{very}\:{stupid}\:{with}\:{that}\:{big} \\ $$$${mouth}\:{u}\:{just}\:{said}\:{u}\:{re}\:{mannerless}\: \\ $$

Commented by Her_Majesty last updated on 05/Sep/20

if you solve an integral the test is the derivation. I have shown your result is not correct. ∫f(x)dx=F(x)+C ⇔ (d/dx)[F(x)+C]=f(x) (d/dx)[F(x)+C]≠f(x) ⇒ F(x)+C≠∫f(x)dx prove that I′m wrong or shut up

$${if}\:{you}\:{solve}\:{an}\:{integral}\:{the}\:{test}\:{is}\:{the} \\ $$$${derivation}. \\ $$$${I}\:{have}\:{shown}\:{your}\:{result}\:{is}\:{not}\:{correct}. \\ $$$$\int{f}\left({x}\right){dx}={F}\left({x}\right)+{C}\:\Leftrightarrow\:\frac{{d}}{{dx}}\left[{F}\left({x}\right)+{C}\right]={f}\left({x}\right) \\ $$$$\frac{{d}}{{dx}}\left[{F}\left({x}\right)+{C}\right]\neq{f}\left({x}\right)\:\Rightarrow\:{F}\left({x}\right)+{C}\neq\int{f}\left({x}\right){dx} \\ $$$${prove}\:{that}\:{I}'{m}\:{wrong}\:{or}\:{shut}\:{up} \\ $$

Commented by mathdave last updated on 05/Sep/20

then proceed to do the correct things let me applaud you for the good work .if u cant keep the fuck up let me see views

$${then}\:{proceed}\:{to}\:{do}\:{the}\:{correct}\:{things}\:{let} \\ $$$${me}\:{applaud}\:{you}\:{for}\:{the}\:{good}\:{work}\:.{if}\:{u} \\ $$$${cant}\:{keep}\:{the}\:{fuck}\:{up}\:{let}\:{me}\:{see}\:{views} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com