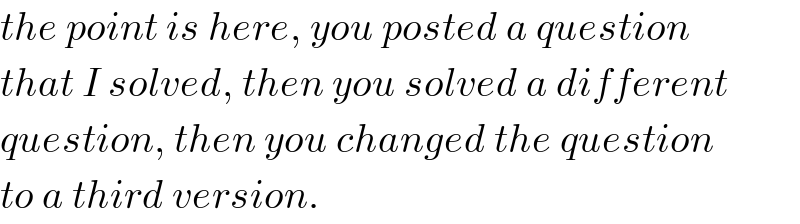solve for x in x^2 +4x=(√(40x^2 +8x−16))


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 111619 by mathdave last updated on 05/Sep/20

$s o l v e f o r x i n$ $x^{2} + 4 x = \sqrt{40 x^{2} + 8 x - 16}$
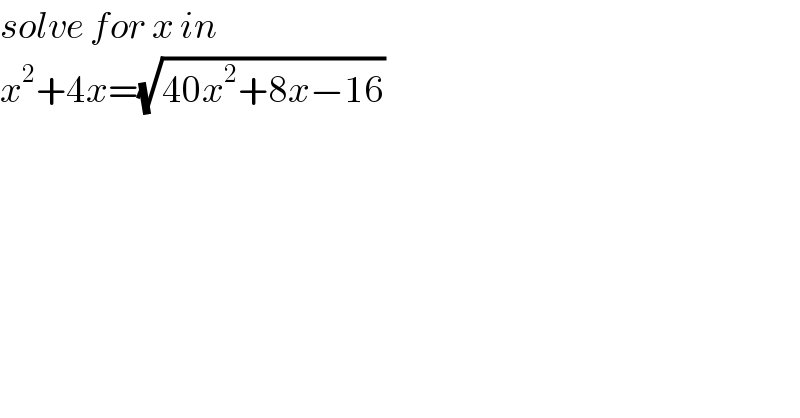
Commented by Her_Majesty last updated on 04/Sep/20

$s q u a r e i t, s o l v e t h e 4^{t h} d e g r e e p o l y n o m i a l$ $a n d c h e c k t h e s o l u t i o n s, 1 o f t h e 3 i s f a l s e$ $e x a c t s o l u t i o n s p o s s i b l e b u t h a r d t o h a n d l e,$ $a p p r o x i m a t i o n g i v e s$ $x_{1} \approx - 10.2894606$ $x_{2} \approx . 914622644$ $x_{3} \approx 2.16142299$
	Answered by mathdave last updated on 04/Sep/20

	$s o l u t i o n$ $l e t x^{2} + 4 x = 2 \sqrt{10 x^{2} + 8 x - 4} . . . . . . . . (1)$ $l e t t^{2} = 10 x^{2} + 8 x - 4$ $t h e n t^{2} = 2 x^{2} + 8 x^{2} + 8 x - 4$ $t^{2} - 8 x^{2} + 4 = 2 x^{2} + 8 x$ $t^{2} - 8 x^{2} + 4 = 2 (x^{2} + 4 x) . . . . . . . . . (2)$ $f r o m (1)$ $x^{2} + 4 x = 2 t . . . . . . . . (x)$ $m u l t i p l y e q u a t i o n (x) b y 2$ $2 (x^{2} + 4 x) = 4 t . . . . . . . . . . (3)$ $e q u a t i n g (2) a n d (3)$ $t^{2} - 8 x^{2} + 4 = 4 t \Rightarrow t^{2} - 4 t - 8 x^{2} + 4 = 0$ $t^{2} - 4 t + 4 - 4 - 8 x^{2} + 4 = 0$ ${(t - 2)}^{2} - 8 x^{2} = 0 \Rightarrow {(t - 2)}^{2} - {(2 \sqrt{2} x)}^{2}$ $(t - 2 - 2 \sqrt{2} x) (t - 2 + 2 \sqrt{2} x) = 0$ $t = 2 + 2 \sqrt{2} x 0 r 2 - 2 \sqrt{2} x$ $b u t t^{2} = 10 x^{2} + 8 x - 4$ ${(2 + 2 \sqrt{2} x)}^{2} = 10 x^{2} + 8 x - 4$ $2 x^{2} + 8 x (1 - \sqrt{2}) - 8 = 0$ $x = \frac{- 4 (1 - \sqrt{2}) \pm \sqrt{64 - 32 \sqrt{2}}}{2}$ $∵ x_{1} = (2 \sqrt{2} - 2) + 2 \sqrt{4 - 2 \sqrt{2}} a n d x_{2} = (2 \sqrt{2} - 2) - 2 \sqrt{4 - 2 \sqrt{2}}$ $a n d a t t = 2 - 2 \sqrt{2} x$ $t h e n (2 - 2 \sqrt{2} x) = 10 x^{2} + 8 x - 4$ $x^{2} + 4 (1 + \sqrt{2}) x - 4$ $x_{3, 4} = 2 (- \sqrt{2} - 1 \pm \sqrt{4 + 2 \sqrt{2}})$ $x_{3} = 2 (- 1 - \sqrt{2} + \sqrt{4 + 2 \sqrt{2}}) a n d x_{4} = - 2 (1 + \sqrt{2} + \sqrt{4 + \sqrt{2}})$ $m a t h d a v e$
	Commented by Her_Majesty last updated on 04/Sep/20

	$b u t t h e q u e s t i o n y o u p o s t e d i s$ $x^{2} + 4 x = \sqrt{40 x^{2} + 3 x - 16}$ $a n d y o u {c a n}^{'} t s o l v e i t t h i s w a y .$
	Commented by Her_Majesty last updated on 04/Sep/20

	$a n y w a y o n e o f y o u r 4 s o l u t i o n s {d o e s n}^{'} t s o l v e$ $t h e e q u a t i o n x^{2} + 4 x = \sqrt{40 x^{2} + 32 x - 16}, s o$ $p l e a s e f i n i s h t h e w o r k$
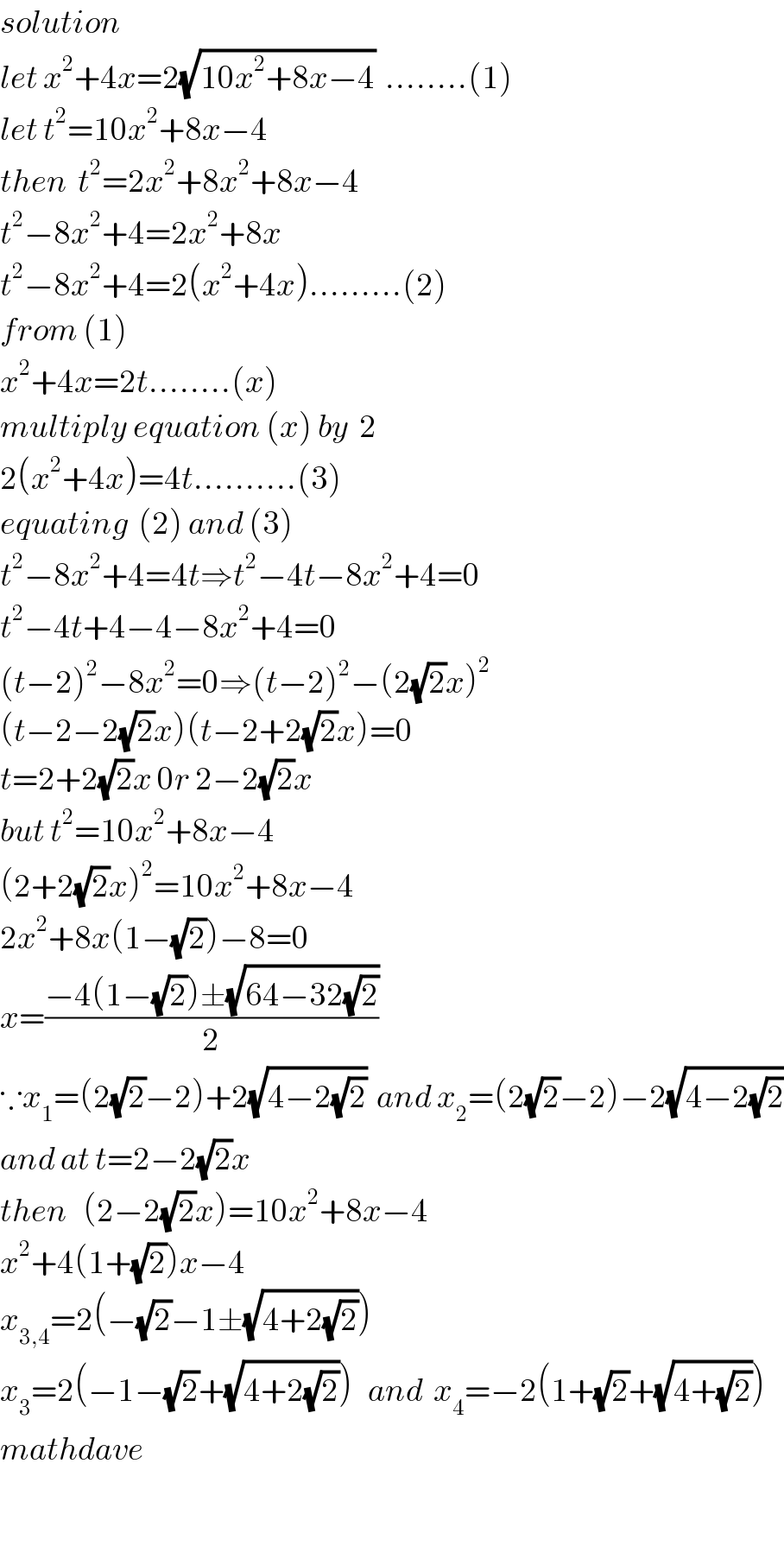
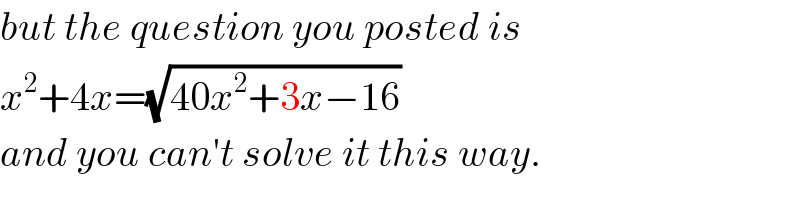
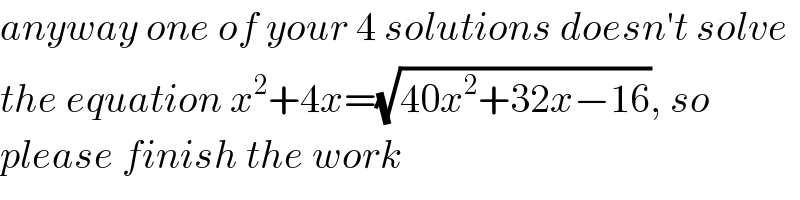
	Commented by Her_Majesty last updated on 04/Sep/20

	$x^{2} + 4 x = \sqrt{40 x^{2} + 32 x - 16}$ $s q u a r i n g a n d t r a n s f o r m i n g$ $x^{4} + 8 x^{3} - 24 x - 32 x + 16 = 0$ $(x^{2} + 4 (1 + \sqrt{2}) x - 4) (x^{2} + 4 (1 - \sqrt{2}) x - 4) = 0$ $x_{1} = - 2 (1 + \sqrt{2} + \sqrt{4 + 2 \sqrt{2}})$ $x_{2} = - 2 (1 + \sqrt{2} - \sqrt{4 + 2 \sqrt{2}})$ $x_{3} = - 2 (1 - \sqrt{2} + \sqrt{4 - 2 \sqrt{2}}) [f a l s e!]$ $x_{4} = - 2 (1 - \sqrt{2} - \sqrt{4 - 2 \sqrt{2}})$
	Commented by Her_Majesty last updated on 05/Sep/20

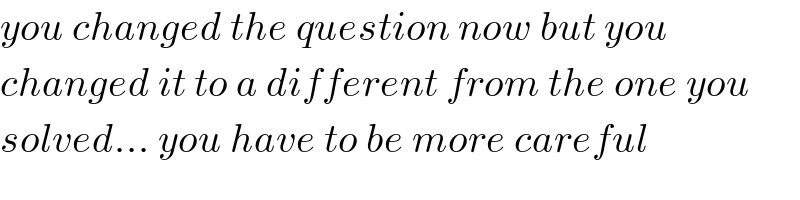
	$y o u c h a n g e d t h e q u e s t i o n n o w b u t y o u$ $c h a n g e d i t t o a d i f f e r e n t f r o m t h e o n e y o u$ $s o l v e d . . . y o u h a v e t o b e m o r e c a r e f u l$
	Commented by mathdave last updated on 05/Sep/20

	$s i n c e u d i s c o v e r e d t h a t o n e o f t h e$ $s o l u t i o n d i d n t s a t i s f y d p r o b l e m t h e n$ $g o a h e a d a n f i x i t$
	Commented by mathdave last updated on 05/Sep/20

	$s t o p m u r m u r i n g$
	Commented by mathdave last updated on 05/Sep/20

	$m o r e c a r e f u l t o w h i c h w a y, a r e u m y t e a c h e r t h a t u a r e c a u t i o n i n g m e$
	Commented by mathdave last updated on 05/Sep/20

	$t h e o n l y w a y i c a n b e l i e v e d a t u k n o w$ $m a t h e m a t i c s i s w h e n u d i s c o v e r e d e r r$ $a n d d o s o m e w o r k i n g o n u r o w n t o a v e r t t h e e r r$ $b u t u s a y i n g i t o r a l l y o r u s i n g a c a l c u l a t o r o r c h e c k i n g$ $w o l f r a m t o d e t e r m i n e t h e a n s w e r d o n t t e l l u k n o w$ $m a t h e m a t i c s$
	Commented by Her_Majesty last updated on 05/Sep/20

	$t h e p o i n t i s h e r e, y o u p o s t e d a q u e s t i o n$ $t h a t I s o l v e d, t h e n y o u s o l v e d a d i f f e r e n t$ $q u e s t i o n, t h e n y o u c h a n g e d t h e q u e s t i o n$ $t o a t h i r d v e r s i o n .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum