Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 111624 by mathdave last updated on 04/Sep/20

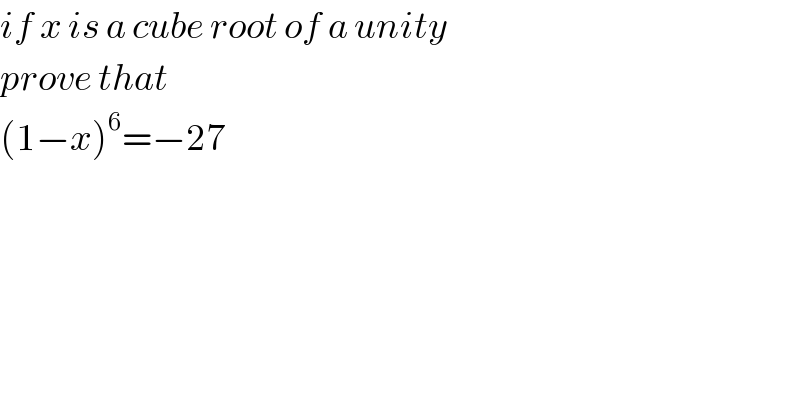
if x is a cube root of a unity prove that (1−x)^6 =−27

$${if}\:{x}\:{is}\:{a}\:{cube}\:{root}\:{of}\:{a}\:{unity} \\ $$$${prove}\:{that}\: \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =−\mathrm{27} \\ $$

Answered by Her_Majesty last updated on 04/Sep/20

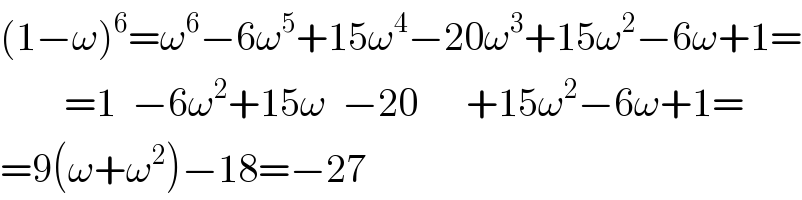
(1−ω)^6 =ω^6 −6ω^5 +15ω^4 −20ω^3 +15ω^2 −6ω+1= =1 −6ω^2 +15ω −20 +15ω^2 −6ω+1= =9(ω+ω^2 )−18=−27

$$\left(\mathrm{1}−\omega\right)^{\mathrm{6}} =\omega^{\mathrm{6}} −\mathrm{6}\omega^{\mathrm{5}} +\mathrm{15}\omega^{\mathrm{4}} −\mathrm{20}\omega^{\mathrm{3}} +\mathrm{15}\omega^{\mathrm{2}} −\mathrm{6}\omega+\mathrm{1}= \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{1}\:\:−\mathrm{6}\omega^{\mathrm{2}} +\mathrm{15}\omega\:\:−\mathrm{20}\:\:\:\:\:\:+\mathrm{15}\omega^{\mathrm{2}} −\mathrm{6}\omega+\mathrm{1}= \\ $$$$=\mathrm{9}\left(\omega+\omega^{\mathrm{2}} \right)−\mathrm{18}=−\mathrm{27} \\ $$

Answered by $@y@m last updated on 04/Sep/20

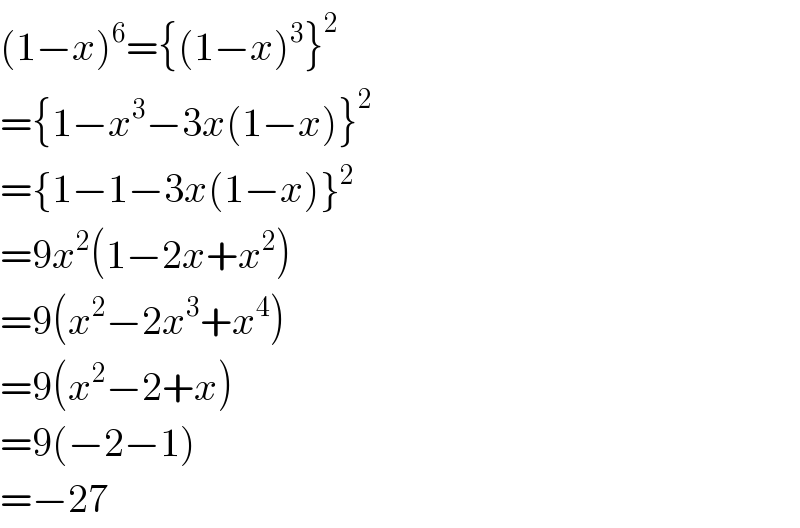
(1−x)^6 ={(1−x)^3 }^2 ={1−x^3 −3x(1−x)}^2 ={1−1−3x(1−x)}^2 =9x^2 (1−2x+x^2 ) =9(x^2 −2x^3 +x^4 ) =9(x^2 −2+x) =9(−2−1) =−27

$$\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =\left\{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} \right\}^{\mathrm{2}} \\ $$$$=\left\{\mathrm{1}−{x}^{\mathrm{3}} −\mathrm{3}{x}\left(\mathrm{1}−{x}\right)\right\}^{\mathrm{2}} \\ $$$$=\left\{\mathrm{1}−\mathrm{1}−\mathrm{3}{x}\left(\mathrm{1}−{x}\right)\right\}^{\mathrm{2}} \\ $$$$=\mathrm{9}{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{9}\left({x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right) \\ $$$$=\mathrm{9}\left({x}^{\mathrm{2}} −\mathrm{2}+{x}\right) \\ $$$$=\mathrm{9}\left(−\mathrm{2}−\mathrm{1}\right) \\ $$$$=−\mathrm{27} \\ $$

Commented by Rasheed.Sindhi last updated on 04/Sep/20

Cool!

$${Cool}! \\ $$

Commented by $@y@m last updated on 04/Sep/20

Thanks

$${Thanks} \\ $$

Answered by mathdave last updated on 04/Sep/20

solution let y^3 =1 y=(1)^(1/3) =(cos(0)+jsin(0))^(1/3) to find the roots let y=(cos2nπ+jsin2nπ)^(1/3) y=(cos((2nπ)/3)+jsin((2nπ)/3)) putting n=0,1,2 which are the roots of the unity at y_n =y_0 =1..........(1) y_1 =[cos((2π)/3)+jsin((2π)/3)]^1 =x ..........(2),at y_2 =[cos((4π)/3)+jsin((4π)/3)]^2 =x^2 ........(3) adding (1),(2), and (3) 1+x+x^2 =1+cos((2π)/3)+jsin((2π)/3)+cos((4π)/3)+jsin((4π)/3) 1+x+x^2 =1+cos(π−(π/3))+jsin(π−(π/3))+cos(π+(π/3))+jsin(π+(π/3)) 1+x+x^2 =1−cos(π/3)+jsin(π/3)−cos((.π)/3)−jsin(π/3) 1+x+x^2 =1−2cos(π/3)=1−2((1/2))=0 1+x+x^2 =0 1+x^2 =−x.........(1) but (1−x)^6 =[(1−x)^2 ]^3 (1−x)^6 =(1−2x+x^2 )^3 =[(1+x^2 )−2x]^3 (1−x)^6 =(−x−2x)^3 =(−3x)^3 (1−x)^6 =−27x^3 but x^3 =1 ∵(1−x)^6 =−27 Q.E.D

$${solution}\: \\ $$$${let}\:{y}^{\mathrm{3}} =\mathrm{1} \\ $$$${y}=\left(\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\left(\mathrm{cos}\left(\mathrm{0}\right)+{j}\mathrm{sin}\left(\mathrm{0}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:{to}\:{find}\:{the}\:{roots}\:{let} \\ $$$${y}=\left(\mathrm{cos2}{n}\pi+{j}\mathrm{sin2}{n}\pi\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${y}=\left(\mathrm{cos}\frac{\mathrm{2}{n}\pi}{\mathrm{3}}+{j}\mathrm{sin}\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right)\:\:\:{putting}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2}\:{which}\:{are}\:{the}\:{roots}\:{of}\:{the}\:{unity} \\ $$$${at}\:\:{y}_{{n}} ={y}_{\mathrm{0}} =\mathrm{1}..........\left(\mathrm{1}\right) \\ $$$${y}_{\mathrm{1}} =\left[\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}+{j}\mathrm{sin}\frac{\mathrm{2}\pi}{\mathrm{3}}\right]^{\mathrm{1}} ={x}\:\:..........\left(\mathrm{2}\right),{at}\: \\ $$$${y}_{\mathrm{2}} =\left[\mathrm{cos}\frac{\mathrm{4}\pi}{\mathrm{3}}+{j}\mathrm{sin}\frac{\mathrm{4}\pi}{\mathrm{3}}\right]^{\mathrm{2}} ={x}^{\mathrm{2}} ........\left(\mathrm{3}\right) \\ $$$${adding}\:\left(\mathrm{1}\right),\left(\mathrm{2}\right),\:{and}\:\left(\mathrm{3}\right) \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}+{j}\mathrm{sin}\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{cos}\frac{\mathrm{4}\pi}{\mathrm{3}}+{j}\mathrm{sin}\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{cos}\left(\pi−\frac{\pi}{\mathrm{3}}\right)+{j}\mathrm{sin}\left(\pi−\frac{\pi}{\mathrm{3}}\right)+\mathrm{cos}\left(\pi+\frac{\pi}{\mathrm{3}}\right)+{j}\mathrm{sin}\left(\pi+\frac{\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} =\mathrm{1}−\mathrm{cos}\frac{\pi}{\mathrm{3}}+{j}\mathrm{sin}\frac{\pi}{\mathrm{3}}−\mathrm{cos}\frac{.\pi}{\mathrm{3}}−{j}\mathrm{sin}\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} =\mathrm{1}−\mathrm{2cos}\frac{\pi}{\mathrm{3}}=\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{1}+{x}^{\mathrm{2}} =−{x}.........\left(\mathrm{1}\right) \\ $$$${but}\:\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =\left[\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \right]^{\mathrm{3}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =\left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} =\left[\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{2}{x}\right]^{\mathrm{3}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =\left(−{x}−\mathrm{2}{x}\right)^{\mathrm{3}} =\left(−\mathrm{3}{x}\right)^{\mathrm{3}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =−\mathrm{27}{x}^{\mathrm{3}} \\ $$$${but}\:\:{x}^{\mathrm{3}} =\mathrm{1} \\ $$$$\because\left(\mathrm{1}−{x}\right)^{\mathrm{6}} =−\mathrm{27}\:\:\:\:\:\:{Q}.{E}.{D} \\ $$$$ \\ $$$$ \\ $$

Commented by Tawa11 last updated on 06/Sep/21

great sir

$$\mathrm{great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com