Previous in Relation and Functions Next in Relation and Functions
Question Number 111755 by mathmax by abdo last updated on 04/Sep/20
$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\:\sqrt{\frac{\mathrm{n}−\mathrm{k}}{\mathrm{n}^{\mathrm{3}} \:+\mathrm{n}^{\mathrm{2}} \mathrm{k}}} \\ $$
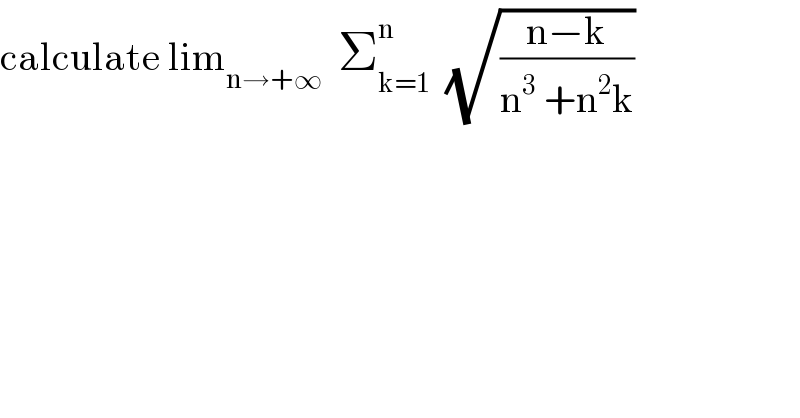
Answered by Dwaipayan Shikari last updated on 04/Sep/20
![(1/n)lim_(n→∞) Σ_(k=1) ^n (√((n−k)/(n+k ))) =(1/n)lim_(n→∞) (√(((1−(k/n))/(1+(k/n))) )) =∫_0 ^1 (√((1−x)/(1+x)))dx =∫_0 ^1 ((1−x)/( (√(1−x^2 )))) =∫_0 ^1 (1/( (√(1−x^2 ))))+(1/2)∫_0 ^1 ((−2x)/( (√(1−x^2 )))) =[sin^(−1) x]_0 ^1 +[(√(1−x^2 )) ]_0 ^1 =(π/2)−1](Q111759.png)
$$\frac{\mathrm{1}}{{n}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\sqrt{\frac{{n}−{k}}{{n}+{k}\:}}\:\:=\frac{\mathrm{1}}{{n}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{\frac{\mathrm{1}−\frac{{k}}{{n}}}{\mathrm{1}+\frac{{k}}{{n}}}\:\:}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$=\left[{sin}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 07/Sep/20
![let S_n =Σ_(k=1) ^n (√((n−k)/(n^3 +n^2 k))) ⇒ S_n =Σ_(k=1) ^n (√((n(1−(k/n)))/(n^3 (1+(k/n))))) =(1/n) Σ_(k=1) ^n (√((1−(k/n))/(1+(k/n)))) →∫_0 ^1 (√((1−x)/(1+x)))dx (S_n is Rieman sum) we do the changement x =cosθ ⇒∫_0 ^1 (√((1−x)/(1+x)))dx =∫_(π/2) ^0 (√((2sin^2 ((θ/2)))/(2cos^2 ((θ/2)))))(−sinθ)dθ =2∫_0 ^(π/2) ((sin((θ/2)))/(cos((θ/2)))) sin((θ/2))cos((θ/2))dθ =∫_0 ^(π/2) 2sin^2 ((θ/2))dθ =∫_0 ^(π/2) (1−cosθ)dθ =(π/2) −[sinθ]_0 ^(π/2) =(π/2)−1 ⇒lim_(n→+∞) S_n =(π/2)−1](Q112255.png)
$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\sqrt{\frac{\mathrm{n}−\mathrm{k}}{\mathrm{n}^{\mathrm{3}} \:+\mathrm{n}^{\mathrm{2}} \mathrm{k}}}\:\Rightarrow\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \sqrt{\frac{\mathrm{n}\left(\mathrm{1}−\frac{\mathrm{k}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\sqrt{\frac{\mathrm{1}−\frac{\mathrm{k}}{\mathrm{n}}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}}}\:\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}\mathrm{dx}\:\:\:\left(\mathrm{S}_{\mathrm{n}} \mathrm{is}\:\mathrm{Rieman}\:\mathrm{sum}\right) \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{cos}\theta\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}\mathrm{dx} \\ $$$$=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \sqrt{\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}}\left(−\mathrm{sin}\theta\right)\mathrm{d}\theta\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)}\:\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{cos}\theta\right)\mathrm{d}\theta\:=\frac{\pi}{\mathrm{2}}\:−\left[\mathrm{sin}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{2}}−\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{S}_{\mathrm{n}} =\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$